Кинетические коэффициенты в жидкости с точки зрения решеточной модели жидкости

В предыдущем параграфе была очень кратко изложена схема получения кинетических коэффициентов в жидкости с использованием методов, разработанных для газовой фазы.

В этом разделе рассмотрим кинетические коэффициенты жидкости, исходя из модели твердого тела. Наиболее известной здесь является теория Эйринга. Эту теорию часто называют теорией абсолютных скоростей реакций, так как первоначально она была использована именно для объяснения законов химической кинетики. Однако позднее данная теория с успехом была применена самим Г.Эйрингом и для вычисления коэффициентов переноса в жидкости, при этом было достигнуто простое и наглядное истолкование процесса. Приведем эти вычисления, но при этом опустим отдельные детали данного подхода, не принципиальные для излагаемого вопроса.

Примем, что частота переходов K молекулы за единицу времени через потенциальный барьер 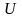пропорциональна³:

. (3.15)

Рассмотрим дырочную модель жидкости: каждая молекула находится в своей ячейке и имеется некоторое количество дырок (рис.3.1).

Рассмотрим подробнее движение одной молекулы к расположенной около нее свободной ячейке (см. рис.3.1).

F

Рис.3.1. Схематический рисунок, поясняющий модель Эйринга

Молекула должна преодолеть горловину (“протиснуться” между верхней и нижней частицами). Если внешняя сила равна нулю, то вид потенциальной энергии U относительно центра горловины симметричен.

Если же возникает сила F, то движение в одном из направлений предпочтительней (в рассматриваемом случае слева направо). Это связано с тем, что возникает добавочная энергия , понижающая барьер U в одном направлении. Частота перескоков в направлении действия силы запишется тогда в виде

,

а для обратного направления:

.

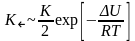Множитель 1/2 возникает по той причине, что при =0 число прыжков частицей вправо и влево должно быть равно K.

Выразим . Пусть – сила, действующая на единицу площади жидкости, тогда сила, действующая на одну молекулу, будет

,

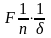где 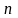- число молекул в единице объема,  - расстояние между соседними слоями. Соответственно работа над молекулой по перемещению ее на расстояние (такой путь надо проделать, чтобы пролезть горловину) равна . Эта работа и совпадает с энергией .

Для общей скорости потока молекул относительно узлов решетки можно записать:

.

Так как, исходя из формулы (3.1):

,

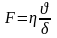то . (3.16)

Из полученного соотношения (3.16) следует, что вязкость рассматриваемой жидкости зависит от внешней силы, т.е. жидкость является не ньютоновской. Отметим, что это редкий случай молекулярной теории переноса в которой заложена возможность описания такого поведения .

Упростим выражение (3.16), считая, что силы малы <<1, тогда, раскладывая знаменатель в ряд, получим:

. (3.17)

Будем приближенно считать, что 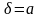, тогда

. (3.18)

Таким образом, для расчета вязкости необходимо определить . Эта энергия по физическому смыслу равна энергии взаимодействия молекулы со своим окружением, и, очевидно, что она должна быть близкой к энергии испарения (несколько меньшей, так как в данном случае молекула разрывает связи не со всем своим окружением, как при испарении). Эмпирически найдено, что она равна:

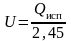, (3.19)

где Q_исп – теплота испарения моля жидкости.

По аналогии получим выражение для коэффициента диффузии. Рассмотрим две площадки 1 и 2 расположенные на некотором малом расстоянии  друг от друга (рис.3.2). Пусть – концентрация вещества, диффузия которого будет изучаться. Предположим, что в слое 1 концентрация равна , тогда в слое 2 из-за малости  концентрация равна (рис.3.2).

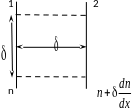
Рис.3.2. Графическое пояснение вывода выражения для коэффициента диффузии

Пусть снова – число перескоков барьера длиной  за единицу времени. Так как площадь, приходящаяся на одну молекулу, , то общее число молекул в единице площади , и поэтому общее число частиц, переходящих через единицу площади за единицу времени в направлении 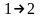, равно . Для обратного направления эта величина, очевидно, равна . В результате суммарный поток частиц за единицу времени через единицу площади оказывается равным:

.

Исходя из формулы (3.3):

. (3.21)

В последнем равенстве использовано, как и прежде, что ³=1/n. Формулу (3.21) также можно непосредственно использовать для вычисления коэффициента диффузии, принимая во внимание явное выражения для K [см. выражения (3.15),(3.19)].

Для вычисления коэффициента теплопроводности предположим, что жидкость имеет ячеечное строение. Пусть молекулы жидкости находятся в узлах кубической решетки и расстояние между ними .

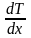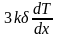Пусть существует температурный градиент . Будем считать, что средняя энергия молекулы в ячейке (представляет собой некий трехмерный гармонический осциллятор). Тогда разность энергии между двумя смежными ячейками в направлении градиента равна - . Предположим, что скорость передачи энергии равна скорости звука . В результате энергия, переданная за единицу времени, равна -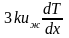 (число элементов ряда в каком-нибудь направлении 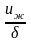умноженное на энергию, вносимую каждым элементом). Общее количество энергии через единицу площади и за единицу времени I_q равно энергии, переданной через отдельный ряд, умноженной на общее число рядов 1/ ²:

.

Вспоминая уравнение (3.2) и используя, как и прежде, связь среднечисловой плотности n с , получим

. (3.22)

Формула (3.22) получила название формулы Бриджмена, она позволяет производить достаточно точный количественный расчет коэффициента теплопроводности в жидкости. Подобная формула была получена ранее. Однако приведенный здесь вывод представляется более последовательным, так как явно не использует формулу для теплопроводности в газе.

ИСХОДНЫЕ ПОЛОЖЕНИЯ НЕРАВНОВЕСНОЙ ТЕРМОДИНАМИКИ.

Локальное равновесие и основное уравнение термодинамики неравновесных процессов

В термодинамически равновесных системах, как известно, температура Т и химический потенциал μ постоянны вдоль всей системы:

Если эти условия не выполняются (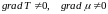 ), то в системе возникают необратимые процессы переноса массы, энергии, электрического заряда и т. д.

При обобщении классической термодинамики на неравновесные процессы исходят из представления о локальном равновесии. Известно, что время релаксации растет с увеличением размеров системы, так что отдельные макроскопически малые части системы приходят сами по себе в равновесное состояние значительно раньше, чем устанавливается равновесие между этими частями. Поэтому в неравновесной термодинамике принимают, что, хотя в целом состояние системы неравновесно, отдельные ее малые части равновесны (точнее, квазиравновесны), но имеют термодинамические параметры, медленно изменяющиеся во времени и от точки к точке.

Размеры этих физически малых равновесных частей неравновесной системы и времена изменения термодинамических параметров в них определяются в термодинамике экспериментально. Обычно принимается, что физический элементарный объем l³, с одной стороны, содержит большое число частиц (v₀ <  l³, v₀ — объем на одну частицу), а с другой стороны, неоднородности макроскопических параметров а_i(r) на длине l малы по сравнению со значением этих параметров , т.е.

Время τ изменения термодинамических параметров в физически малых равновесных частях намного больше времени τ_l релаксации в них и намного меньше времени τ_L, за которое устанавливается равновесие во всей системе:

.

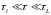В условиях, когда допустимо такое представление о локальном равновесии, можно построить последовательную феноменологическую термодинамику необратимых процессов. Свойства неравновесной системы при этом определяются локальными изменениями по пространственным координатам и времени через характеристические термодинамические параметры, для которых справедливы уравнения термодинамики. Так, если в качестве характеристических переменных выбраны локальная плотность внутренней энергии 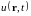, удельный объем ) ( 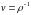, ρ – локальная плотность массы среды) и локальные концентрации 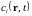различных компонентов, то состояние физически элементарного объема в окрестности точки r в момент времени t описывается локальной энтропией , определяемой уравнением Гиббса

(1)

Объединяющее первое и второе начала термодинамики уравнение (1) для удельных (по массе) локальных величин является основным уравнением неравновесной термодинамики. Так как локальная энтропия s (единицы массы или ρs – единицы объема) зависит от термодинамических параметров так же, как и при полном равновесии, то при необратимом процессе в адиабатной системе (теплоизолированная система, которая не обменивается с окружающей средой энергией в форме теплоты) скорость возникновения энтропии в единице объема (производство энтропии) равна

Рассматривая увеличение энтропии при изменении локальных макроскопических параметров а_i в адиабатных условиях как ≪причину≫ необратимого процесса, величины называют термодинамическими силами, а величины , определяющие скорость изменения параметров а_i – термодинамическими потоками. Выражение для производства энтропии с такими определениями можно записать в виде

.

Энтропия всей неравновесной системы аддитивно складывается из энтропий ее отдельных частей:

.

Уравнения баланса и законы сохранения различных величин.

Для определения с помощью основного уравнения термодинамики неравновесной системы производства энтропии и изменения во времени всех других ее термодинамических функций к этому уравнению необходимо добавить уравнения баланса ряда величин (массы, внутренней энергии и др.), а также уравнения, связывающие потоки 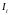этих величин с термодинамическими силами . Найдем уравнения баланса и законы сохранения различных величин в общем виде. Это поможет нам понять, что может выступать в роли термодинамических сил.

Всякая экстенсивная (пропорциональная размерам системы, например, масса, внутренняя энергия. Полное значение для системы определяется сложением значений всей сстемы) величина В(х, у, z , t) макроскопической системы подчиняется уравнению баланса

,

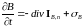где — плотность полного потока величины В = ρb (ρ — плотность вещества, b — значение величины В, отнесенное к массе), 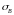— изменение В за счет ее источников, отнесенное к объему и времени.

Если в этом уравнении равно нулю, то оно выражает закон сохранения величины В. Так, закон сохранения массы имеет вид гидродинамического уравнения непрерывности

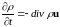
где u— массовая скорость в данной точке в момент времени t.

Плотность полного потока , вообще говоря, не сводится к конвективному потоку Вu, т. е. к переносу величины В с потоком вещества, а содержит также члены другой природы (тепловой поток, диффузионный поток и т. д.):

,

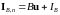( – неконвективная часть потока).

Таким образом, уравнение баланса аддитивной величины можно записать в виде

где частная производная 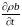определяет изменение величины В в данной неподвижной точке пространства. Эту производную можно выразить через полную (субстанциальную) производную величины В, относящуюся к передвигающейся в пространстве «частице» вещества (как сплошной среды). Для этого заметим, что изменение dВ величины В частицы вещества складывается из двух частей: из изменения В в данном месте пространства со временем и из изменения В при переходе от данной точки к другой точке, удаленной от нее на расстояние dr, пройденное рассматриваемой частицей вещества в течение времени dt. Первая из этих частей равна , а вторая часть равна

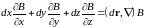
Следовательно,

.

Поэтому закон сохранения массы и уравнение баланса величины В можно записать соответственно в виде

,

.

В соответствии с общей формулой уравнение баланса энтропии будет

,

где I_s — плотность потока энтропии, σ— локальная скорость возникновения энтропии.

Для нахождения явного вида I_s и σ уравнение баланса энтропии сопоставляют с выражением для , получаемым из уравнения Гиббса:

Рассмотрим пример. Найдем уравнение баланса энтропии с явным видом для I_s и σ в однородном твердом теле, в котором имеется градиент температуры.

Пусть — удельная внутренняя энергия. Изменением объема тела вследствие теплового расширения будем пренебрегать; поток частиц в случае твердого тела также исключен. Поэтому из имеем

.

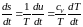По закону сохранения энергии (в соответствии с общей формулой при  = 0),

,

где 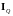— плотность потока теплоты. Из этих уравнений для баланса энтропии получаем

,

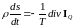и так как

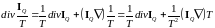
то

.

Сопоставляя это уравнение с гидродинамическим уравнением баланса энтропии , находим, что плотность потока энтропии I_s и производство энтропии σ соответственно равны

,

где – декартова компонента термодинамическом силы, соответствующая декартовой координате потока I_i.

Линейный закон. Соотношения взаимности Онсагера и принцип Кюри.

В равновесном состоянии термодинамические силы Х_i, потоки I_i и производство энтропии σ равны нулю. Поэтому при малых отклонениях от равновесия естественно положить линейную связь между потоками и силами

.

Коэффициенты L_ik в этом линейном законе называются феноменологическими или кинетическими коэффициентами. Причем диагональные коэффициенты L_ii определяют ≪прямые≫ явления переноса, а недиагональные коэффициенты L_ik, непрерывно связанные с прямыми, — ≪перекрестные≫ или ≪сопряженные≫ процессы. Так, по закону теплопроводности Фурье градиент температуры вызывает поток теплоты и L_ii =ϰ; по закону Фика градиент концентрации вызывает диффузию I = –D grad с, L = D; по закону Ома градиент потенциала вызывает ток j = –σ grad φ, L = σ (удельная проводимость) и т. д. Наряду с этими прямыми процессами переноса возникают и сопряженные с ними процессы. Например, при существовании градиента температуры кроме переноса теплоты может происходить и перенос массы (термодиффузия). Такие перекрестные процессы характеризуются недиагональными коэффициентами L_ik. Так, плотность потока массы I₁, при наличии градиента концентрации и градиента температуры равна

.

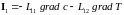Потоки I_i и силы X_i не могут быть выбраны произвольно. Они должны быть такими, чтобы выполнялось равенство .

В линейный закон входит большое число феноменологических параметров L_ik. Однако число независимых этих коэффициентов удается уменьшить, если учесть соображения временной и пространственной симметрии.

В 1931 г. Онсагер, исходя из инвариантности микроскопических уравнений движения относительно изменения знака времени (временная симметрия) и из представления о неравновесном состоянии системы, вызванном внешними силами, как крупной флуктуации равновесной системы, установил, что в области линейности необратимых процессов матрица кинетических коэффициентов симметрична:

.

Физически этот закон термодинамики линейных необратимых процессов означает, что имеется некоторая симметрия во взаимодействии различных процессов: возрастание потока I_k, обусловленное увеличением на единицу силы X_i (при постоянных X_k≠i), равно возрастанию потока I_i, обусловленному увеличением на единицу X_k.

Ряд свойств кинетических коэффициентов можно установить исходя непосредственно из термодинамических законов линейных необратимых процессов. Действительно, для таких процессов общая формула для производства энтропии принимает квадратичное по термодинамическим силам выражение

,

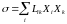и из того условия, что для необратимых процессов , можно вывести, например, что .

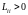Дальнейшие упрощения матрицы феноменологических коэффициентов (уменьшение их числа) можно получить при учете симметрии среды. В выражение линейного закона входят потоки и силы, из которых одни являются скалярными (в процессах с химическими реакциями, а также с объемной вязкостью), другие — векторами (потоки массы и теплоты), а третьи – тензорами (в процессах со сдвиговой вязкостью). В зависимости от симметрии среды система линейных уравнений должна быть инвариантна относительно соответствующих ортогональных преобразований. При преобразованиях компоненты входящих в (14.1) различных величин преобразуются по-разному, в то время как установленная связь между потоком и силой не может изменяться при преобразованиях. Это приводит в случае изотропных систем к сохранению связей лишь между потоками и силами одной тензорной размерности, что выражает принцип Кюри о сохранении симметрии причины в симметрии следствий. Поэтому, хотя согласно линейному закону (14.1) каждая декартова компонента потока I_i может зависеть от декартовых компонент всех термодинамических сил, по принципу Кюри в зависимости от структуры (симметрии) среды может оказаться, что компоненты потоков будут зависеть не от всех компонент термодинамических сил и, следовательно, не все причины вызывают перекрестные эффекты. Например, в результате химической реакции (скалярный процесс) не может возникнуть диффузионный поток (векторный процесс).

Основное уравнение неравновесной термодинамики при использовании линейного закона и соотношений взаимности Онсагера позволяет установить общие связи между кинетическими коэффициентами различных процессов переноса в рассматриваемой системе.

Термомеханический и механокалорический эффекты

Термомеханический эффект состоит в возникновении разности давлений dp=p₂—p₁ в резервуарах с жидкостью, соединенных капилляром, при поддержании в них разности температур dT = T₂— T₁. В случае, когда резервуары отделены один от другого пористой перегородкой, этот эффект называется термоосмосом. Мы уже рассматривали его для ультраразреженного газа.

Явление, обратное термомеханическому эффекту, т. е. появление разности температур в результате создания разности давлений в сосудах, называется механокалорическим эффектом.

Рассмотрим теорию этих двух необратимых явлений. Пусть два сосуда 1 и 2 поддерживают при постоянных температурах Т и T+dT. Обозначим: I₁ — поток энергии между сосудами, I₂ — возможный поток вещества. Соответствующие этим потокам силы, согласно формуле (14.28), равны (хотя это и не очевидно, приведем формулы без доказательства)

.

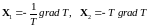По линейному закону

В стационарном состоянии поток I₂ равен нулю, а поток энергии I₁ остается постоянной величиной. Поэтому из формул получаем

,

.

Для однокомпонентной жидкости

,

где V и H – объем и энтальпия (энтальпия — это та энергия, которая доступна для преобразования в теплоту при определенном постоянном давлении) моля жидкости.

.

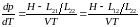Из этого выражения видно, что термомеханический эффект будет существовать только тогда, когда молярная энтальпия жидкости не равна дроби . Для выяснения смысла этой дроби рассмотрим два сосуда при одинаковой температуре (сила X₁ равна нулю). Тогда из уравнения получаем

,

то есть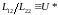

– энергия переноса (энергия, перенесенная единицей массы из сосуда 1 в 2 при изотермическом процессе).

При таком переносе энергии в сосуде 1 поддерживаются постоянными температура Т и давление р за счет поглощения теплоты Q* от внешнего теплоисточника и совершения работы. Поэтому изменение внутренней энергии жидкости в сосуде 1 при выходе из него моля жидкости по первому началу равно

,

откуда .

Количество теплоты , поглощенное в сосуде 1 молем жидкости, перенесенной из сосуда 1 в сосуд 2 при постоянных температуре и разности давлений, называется теплотой переноса. Таким образом,

(1)

и, следовательно, при положительном значении Q* в стационарном состоянии более высокое давление устанавливается там, где более низкая температура.

Ранее мы рассматривали эффект Кнудсена для стационарного состояния разреженных идеальных газов с разной температурой в двух сосудах, соединенных малым отверстием. Очевидно, что это частный случай вышеприведенного рассмотрения. На основании кинетической теории можно найти, что энергия переноса на моль газа равна

,

а молярная энтальпия

.

Поэтому теплота переноса

(2)

имеет отрицательноезначение.

Подставляя выражение (2) в (1), получим соотношение Кнудсена:

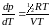
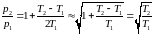
т. e. при соединении капилляром двух сосудов с ультраразреженными газами (длина свободного пробега молекул больше размеров сосуда) с разной температурой давление будет больше в том сосуде, который горячее.

В обычном случае идеального газа, т. е. когда отверстие между сосудами так велико, что газ проходит макроскопическим потоком, энергия переноса U* включает кроме внутренней энергии U еще и работу pV, так что

.

10. Поверхностное натяжение. Капиллярные явления

Свободная поверхностная энергия.

Жидкое состояние возникает тогда, когда потенциальная энергия притяжения молекул превосходит по абсолютному значению их кинетическую энергию. Силы притяжения между молекулами в жидкости значительны и обеспечивают удержание молекул в объеме жидкости. Таким образом, у жидкости образуется поверхность, которая ограничивает ее объем. Разберемся, какой будет эта поверхность, которая, очевидно, зависит от формы объема жидкости.

Жидкости занимают промежуточное состояние между газами и кристаллами и сочетают в себе некоторые свойства обоих этих состояний. В жидкостях имеет место так называемый ближний порядок: относительно рассматриваемой молекулы упорядоченно располагаются лишь ближайшие соседи, отстоящие на расстоянии 2-3 межатомных интервалов. Примерно на такое же расстояние распространяется заметное взаимодействие между молекулами.

М олекулу 1, находящуюся внутри жидкости, ближайшие соседи окружают со всех сторон. Она испытывает притяжение со стороны всех соседних с ней молекул. При этом их притяжение взаимно компенсируется. Молекулу 2, находящуюся у поверхности жидкости, ближайшие соседи окружают только с одной стороны. На такие частицы вблизи поверхности жидкости со стороны других молекул жидкости действуют силы, равнодействующая которых направлена внутрь жидкости, нормально к поверхности. Эта сила консервативная, поэтому при перемещении молекулы из какой-либо внутренней точки жидкости в точку поверхностного слоя эта сила совершает работу А, которая равна приращению потенциальной энергии молекулы:

.

Так как A<0 (работу нужно затратить), то W_p2 > W_p1.

Таким образом, каждая молекула, находящаяся на поверхности жидкости, обладает избыточной потенциальной энергией по сравнению с молекулами, находящимися внутри жидкости.

Поскольку всякая система стремится перейти в состояние с минимальной потенциальной энергией, то жидкость (под действием втягивающих сил) принимает такую форму, при которой площадь ее поверхности минимальна. При отсутствии других сил (например, в невесомости) такой фигурой является шар. Если жидкость находится в поле сил тяготения, то она принимает форму, соответствующую минимуму суммарной энергии – в поле сил тяготения и поверхностной энергии.

Если мы рассмотрим маленькую каплю, то ее поверхностная энергия (пропорциональная площади поверхности, определяемой квадратом линейных размеров) будет больше, чем энергия в поле сил тяготения (которая пропорциональна объему тела, то есть кубу линейных размеров). Поэтому маленькие капли принимают близкую к сферической форму. Но при увеличении объема начинает преобладать энергия в поле сил тяготения, поэтому капли сплющиваются под действием сил тяжести.

Свойство жидкости сокращать свою свободную поверхность называется поверхностным натяжением. Коэффициент поверхностного натяжения – СФВ, характеризующая свойство жидкости сокращать свою свободную поверхность, и равная отношению модуля силы поверхностного натяжения, действующей на границу поверхностного слоя, к длине этой границы:

.

Оно зависит от свойств жидкости и варьируется в широких пределах. У большинства жидкостей поверхностное натяжение имеет при 20°С порядок от 10^-2 до 10^-1 Н/м.

Механизм возникновения поверхностного натяжения. Свободная энергия, характеризуемая σ, сосредоточена в небольшом поверхностном слое жидкости, поэтому и силы поверхностного натяжения действуют только в тонком поверхностном слое. В этом отношении тонкий поверхностный слой действует наподобие резиновой оболочки, которой окружен объем жидкости. Разница с резиновой оболочкой состоит лишь в том, что она имеет постоянное натяжение независимо от того, как изменяется поверхность жидкости в результате изменения формы занимаемого ею объема.

П оверхностное натяжение зависит от свойств вещества, с которым соприкасается поверхность жидкости. Это особенно очевидно из интерпретации σ как плотности свободной энергии, поскольку вещество у поверхности жидкости также воздействует на молекулы поверхностного слоя жидкости и, следовательно, изменяет силы, втягивающие их внутрь жидкости. Это означает, что поверхностное натяжение σ изменяется. Поэтому, когда идет разговор о поверхностном натяжении, надо указывать не только жидкость, которая имеется в виду, но и вещество, с которым поверхность жидкости соприкасается, т. е. σ должна быть снабжена двумя индексами, указывающими две граничащие между собой среды. Ясно, что поверхностное натяжение на поверхности раздела двух жидкостей должно быть меньше, чем на свободной поверхности. На поверхности раздела твердого тела с жидкостью поверхностное натяжение также уменьшается.

Условия равновесия на границе двух жидкостей. Если на поверхность одной жидкости поместить каплю другой, более легкой, то возможны два результата в зависимости от соотношения поверхностных натяжений. Если обозначить dl элемент длины, направленный вдоль линии соприкосновения трех сред 1, 2, 3, то силы поверхностного натяжения, действующие на этот элемент, равны σ₁₂dl, σ₂₃dl, σ₁₃dl. Заметим, что элемент dl направлен перпендикулярно плоскости чертежа. Если σ₁₃ < σ₂₃ + σ₁₂ то равновесие реализуется в виде ситуации, изображенной на рис. 78, а. Условием равновесия является обращение в нуль равнодействующих всех сил, действующих на элемент dl:

Система этих уравнений позволяет определить углы и , которые называются краевыми.

Если же σ₁₃ > σ₂₃ + σ₁₂, то равновесная ситуация указанного вида невозможна и капля 2 растечется по всей поверхности жидкости 1 в виде тонкого молекулярного слоя

Условия равновесия на границе жидкость — твердое тело.

В этом случае возможны равновесные ситуации, показанные на рис. Условия равновесия при этом имеют соответственно вид

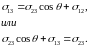
Если σ₁₃ > σ₂₃ + σ₁₂, то жидкость растекается по поверхности молекулярным слоем. Это случай полного смачивания. На первом рисунке приведен пример частичного смачивания, на втором – полного несмачивания.

Если жидкость налита в сосуд, то форма жидкости при соприкосновении с вертикальными стенками сосуда различна в зависимости от того, смачивает жидкость стенки сосуда или не смачивает.

Если краевой угол удовлетворяет условию 0 < Θ < 90, имеет место частичное смачивание жидкостью поверхности твердого тела. В этом случае силы взаимодействия между молекулами жидкости и твердого тела больше сил взаимодействия между молекулами жидкости. Если 90 < Θ < 180, имеет место частичное несмачивание жидкостью поверхности твердого тела. В этом случае силы взаимодействия между молекулами жидкости и твердого тела меньше сил взаимодействия между молекулами жидкости.

П ри плавании тел в жидкости из-за эффектов смачивания и несмачивания возникают дополнительные силы, которые либо увеличивают подъемную силу, либо уменьшают ее. Когда жидкость смачивает твердое тело, то поверхностное натяжение направлено против подъемной силы и стремится погрузить тело в жидкость. Когда жидкость не смачивает твердое тело, поверхностное натяжение направлено вверх и стремится вытолкнуть тело из жидкости. Эти дополнительные силы за счет поверхностного натяжения обычно невелики по сравнению с силами Архимеда. Но бывают ситуации, когда они существенны. Например, если плотность плавающего тела лишь незначительно превосходит плотность жидкости, а его линия соприкосновения с поверхностью жидкости достаточно велика, то может случиться, что тело не утонет исключительно из-за поверхностного натяжения, если тело не смачивается жидкостью. Известны насекомые, которые бегают по поверхности воды и при этом не тонут за счет поверхностного натяжения воды.

Давление под искривленной поверхностью. Формула Лапласа.

Искривленный поверхностный слой оказывает на жидкость дополнительное давление. (Такое искривление называется мениском.)

В случае выпуклого мениска поверхностный слой, стремясь сократиться, сжимает жидкость, в случае вогнутого мениска – растягивает ее. Рассмотрим простейший случай, когда жидкость находится в вертикальной цилиндрической трубке радиуса r и не смачивает ее стенки. Мениск в этом случае представляет собой полусферу, обращенную выпуклостью вверх. Сила давления поверхностного слоя, действующая на жидкость, направлена вертикально вниз и равна по модулю F=2πrσ. Для нахождения добавочного давления эту силу нужно разделить на площадь поперечного сечения трубки πr². В результате получим:

.

Формула называется формулой Лапласа, а давление p_Л – лапласовым давлением. Под выпуклым мениском лапласово давление положительно, под вогнутым – отрицательно.

Приведем вывод формулы Лапласа для случая мыльного пузыря. Резиновый шар или мыльный пузырь могут оставаться в равновесии, только если давление внутри них на определенную величину больше, чем давление снаружи. Вычислим это превышение. Пусть мыльный пузырь имеет радиус R и пусть избыток давления внутри него равняется p.

Чтобы увеличить объем пузыря на малую величину dV, нужно затратить работу pdV, которая идет на увеличение энергии поверхности пузыря. Можно показать, что коэффициент поверхностного натяжения имеет смысл энергии, приходящейся на единицу поверхности жидкости. Увеличение энергии в таком случае равно:

,

где σ – коэффициент поверхностного натяжения. (Коэффициент 2 в формуле появляется потому, что у пузыря две поверхности). Таким образом, получим:

.

Имея в виду, что

и ,

Получим:

.

У капли будет одна поверхность, соответственно для нее получим формулу с коэффициентом 2.

В общем случае отсутствия сферической симметрии кривизна поверхности определяется двумя главными радиусами кривизны R₁ и R₂. При этом давление дается выражением

.

(средняя кривизна поверхности)

Капиллярные явления.

При взаимодействии со стенкой сосуда силы поверхностного натяжения стремятся либо поднять уровень жидкости, либо опустить его. Если стенки трубки смачиваются жидкостью, то жидкость в ней поднимается, если не смачиваются, то опускается.

Выведем формулу для высоты h, на которую поднимается жидкость в капилляре в случае смачивания. Давление в капилляре на уровне свободной поверхности жидкости в широком сосуде равно атмосферному. Но в капилляре из-за поверхностного натяжения есть капиллярное/лапласово давление. Поэтому между жидкостью в капилляре и широком сосуде устанавливается такая разность уровней h, чтобы гидростатическое давление уравновешивало капиллярное:

.

Окончательно получаем:

.

Радиус кривизны мениска r можно выразить через краевой угол и радиус капилляра R. Из рисунка видно, что . Следовательно,

.

Чем меньше радиус трубки, тем выше поднимается по ней жидкость в случае смачивания. Поэтому такой эффект называется капиллярным.

Одним из механизмов подъема воды деревьями является как раз капиллярный.

1 В физике консервати́вные си́лы (потенциальные силы) — это силы, работа которых не зависит от вида траектории, точки приложения этих сил и закона их движения, и определяется только начальным и конечным положением этой точки^[1]. Равносильным определением является и следующее: консервативные силы — это такие силы, работа которых по любой замкнутой траектории равна 0.

В теоретической физике выделяют только четыре типа сил, каждая из которых является консервативной (см. Фундаментальные взаимодействия). В школьной программе по физике силы разделяют на консервативные и неконсервативные. Примерами консервативных сил являются: сила тяжести, сила упругости, сила кулоновского (электростатического) взаимодействия. Примером неконсервативной силы является сила трения.

Если в системе действуют только консервативные силы, то механическая энергия системы сохраняется.

2 При движении под действием центральной силы момент вектора скорости v относительно центра О будет величиной постоянной. По сути, следствие закона сохранения момента импульса в поле центральной силы.

3 Коэффициент пропорциональности kT/h, где h – постоянная Планка.

132