10. Времена релаксации.

В результате явлений переноса происходит выравнивание температур и концентраций, т. е. температура и концентрация изменяются с течением времени. Если система предоставлена самой себе, то температуры и концентрации по всему объему газа должны быть постоянными. Время, в течение которого это происходит, называется временем релаксации системы. А для анализа изменения величин во времени необходимо иметь уравнения теплопроводности и диффузии, зависящие от времени.

Найдем уравнение диффузии, зависящее от времени. Рассмотрим самодиффузию, поток которой дается уравнением

.

Выделим объем V в виде цилиндра, площадь основания которого ∆S, а высота, направленная вдоль оси X, равна ∆х. По определению потока, и зменение числа частиц в объеме цилиндра в течение промежутка времени ∆t равно

.

Разлагая поток в ряд Тейлора и ограничиваясь линейными членами по ∆х, получаем

,

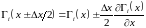следовательно, можно заисать

.

Тогда

.

Поскольку коэффициент диффузии не зависит от координат, можно записать

.

Это нестационарное уравнение самодиффузии. Если направление диффузии не совпадает с осью X, а имеет произвольное направление, то ∆N₁ в формуле представляется в виде суммы вкладов по каждой из осей координат и вместо уравнения полученного уравнения имеем

.

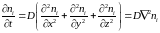Зная начальное распределение концентрации во всем объеме в начальный момент времени (начальные условия) и при заданных граничных условиях можно определить изменение концентрации n_i молекул во всех точках объема.

Отметим, что если рассматривается взаимодиффузия, то вместо уравнения необходимо пользоваться уравнением с коэффициентом диффузии D₁₂. Тогда в результате аналогичных вычислений для каждой из компонент получается похожее уравнение с коэффициентом диффузии D₁₂, . Однако этот коэффициент зависит от координат и нельзя совершить переход к уравнению вида . Необходимо решать систему двух нелинейных уравнений.

Аналогичные зависимости получаются и для теплопроводности, просто вместо потока частиц берется поток тепла. Ранее мы получали, что ,

где ϰ =  – коэффициент теплопровоности газа. Тогда, с учетом того, 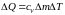– это изменение количества теплоты в объеме за время , можно записать

,

или .

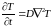Что касается времени релаксации. При отклонении некоторой величины от равновесного значения возникают факторы, стремящиеся вернуть ее к этому значению. Скорость приближения величины к равновесному значению считается пропорциональной ее отклонению от равновесного значения. Обратная величина коэффициента пропорциональности является временем релаксации.

Пусть рассматривается величина q, равновесное значение которой q₀. Тогда высказанное выше определение может быть записано следующим образом:

.

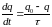Решение этого уравнения имеет вид

,

где 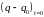– отклонение от равновесного значения в начальный момент времени. В соответствии с общим условием об экспоненциально изменяющихся величинах, τ имеет смысл времени достижения величиной q равновесного значения, т. е. времени релаксации.

Время релаксации для концентрации.

Допустим, что в некотором объеме, линейные размеры которого имеют порядок L, а объем — порядок L³, концентрация или температура отличны от окружающей среды. Тогда через поверхность объема устремится либо тепловой поток, либо поток частиц, чтобы сделать концентрацию и температуру равными их значениям в окружающей среде. Исследуем закон, по которому происходит выравнивание этих величин, взяв в качестве примера концентрацию частиц. Ясно, что в результате совпадения уравнений для диффузии и теплопроводности закон выравнивания температур аналогичен.

Если <∆n> — среднее отклонение концентрации частиц от равновесной в объеме V, то V<∆n > — это избыток числа частиц в объеме по сравнению с числом частиц, соответствующим равновесной плотности. Поток частиц через поверхность, ограничивающую объем, положителен, если имеется избыток частиц внутри объема, и отрицателен, если имеется недостаток. Поэтому изменение числа частиц внутри объема в течение времени dt равно

где S — площадь поверхности, ограничивающей объем; — средний поток частиц через поверхность. Если L — линейные размеры области, то и из уравнения следует, что

.

Положительный знак правой части уравнения учитывает, что при положительно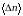м поток должен быть положителен. Объединяя две формулы, получим

.

Решение этого уравнения имеет вид

Величина

является временем релаксации к равновесному распределению концентраций. Поскольку V~ L³, S ~ L², заключаем, что τ ~ L²/D. Это показывает, что время релаксации сильно растет с увеличением геометрических размеров области. Оно также обратно пропорционально коэффициенту диффузии, посредством которого связывается с температурой и давлением газа.

Для времени релаксации температуры расчет аналогичен, в результате получим зависимость

.
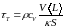