
- •Давление жидкости. Закон Паскаля. Закон Архимеда
- •Барометрическая формула.
- •Стационарное течение жидкости по прямолинейной трубе. Формула Пуазейля.
- •Средняя длина свободного пробега.
- •Эффективное сечение.
- •Распределение молекул по длинам свободного пробега.
- •Внутреннее трение и теплопроводность газов.
- •Самодиффузия в газах.
- •Связь коэффициента диффузии с подвижностью частицы
- •Концентрационная диффузия в газах
- •Броуновское движение как процесс диффузии
- •Термическая диффузия в газах
- •Времена релаксации.
- •Явления в разреженных газах.
- •Теплопроводность и диффузия в жидкостях.
- •Кинетические коэффициенты в жидкости с точки зрения решеточной модели жидкости
Термическая диффузия в газах
Если концы прямолинейной трубы, заполненной однородной смесью двух различных газов, имеют разные температуры, то вдоль трубы возникают диффузионные потоки этих газов, направленные в противоположные стороны. Направления потоков определяются следующим правилом. Если массы молекул т1 и т2 не слишком близки, то более массивные молекулы стремятся перейти в более холодные области, а менее массивные — в более нагретые. В большинстве случаев в более теплых областях объема увеличится концентрация легкой компоненты смеси, а в более холодных — тяжелой, хотя и не всегда.
Если же т1 и т2 почти одинаковы, но молекулы имеют разные размеры, то в холодные области устремляются более крупные молекулы, а в теплые — менее крупные. Описанное явление называется термической диффузией или, короче, термодиффузией.
С
феноменологической точки зрения
возникновение потока частиц под влиянием
градиента температуры совершенно
естественно. Но по своей природе
термодиффузия отличается от ранее
рассмотренных процессов переноса,
которые обусловливались самим фактом
столкновения молекул между собой.
Термодиффузия обусловливается не самим
фактом столкновения молекул, а зависимостью
частоты столкновений между молекулами
от их скорости. Направление термодиффузионного
потока существенно зависит от характера
взаимодействия между молекулами.
Например, если представить силы
отталкивания между молекулами в виде
 ,
то,
как показывает строгая теория,
термодиффузионные потоки меняют знак
при переходе через v = 5.
При
v = 5
термодиффузия отсутсвует. При v > 5
термодиффузия происходит так, что более
горячие области обогащаются более
легкой компонентой, а при v < 5
— более тяжелой. Интересно отметить,
что Максвеллом при его расчетах был
принят закон
,
то,
как показывает строгая теория,
термодиффузионные потоки меняют знак
при переходе через v = 5.
При
v = 5
термодиффузия отсутсвует. При v > 5
термодиффузия происходит так, что более
горячие области обогащаются более
легкой компонентой, а при v < 5
— более тяжелой. Интересно отметить,
что Максвеллом при его расчетах был
принят закон
 ,
так как в этом случае вычисления сильно
упрощаются и становятся выполнимыми.
Поэтому-то термодиффузия осталась им
незамеченной. Это явление теоретически
было предсказано независимо друг от
друга Энскогом и Чепменом в 1917 г. На
опыте термодиффузия в газах наблюдалась
Чепменом и Дутсоном в том же году. Строгие
теории термодиффузии Энскога и Чепмена
очень сложны и громоздки. Мы ограничимся
лишь главными моментами в рассмотрении
этого вопроса.
,
так как в этом случае вычисления сильно
упрощаются и становятся выполнимыми.
Поэтому-то термодиффузия осталась им
незамеченной. Это явление теоретически
было предсказано независимо друг от
друга Энскогом и Чепменом в 1917 г. На
опыте термодиффузия в газах наблюдалась
Чепменом и Дутсоном в том же году. Строгие
теории термодиффузии Энскога и Чепмена
очень сложны и громоздки. Мы ограничимся
лишь главными моментами в рассмотрении
этого вопроса.
В результате термодиффузии происходит частичное разделение газовой смеси и связанное с ним возникновение градиентов концентрации каждого из компонентов. Это вызывает концентрационную диффузию, стремящуюся устранить указанное разделение. Если концы трубы поддерживаются при постоянных температурах, то в трубе в конце концов установится стационарное состояние с вполне определенным распределением температуры и концентрации. Чтобы вы представляли порядки величин, допустим, например, что на концах трубы, заполненной однородной смесью, состоящей из 50% молекул O2 и 50% молекул N2, поддерживаются температуры 0 и 500° С. Тогда, как показывает опыт, в установившемся состоянии у более нагретого конца будет 50,27% N2 и 49,73% O2, а у более холодного 49,73% N2 и 50,27% O2.
В стационарном состоянии при наличии небольшого градиента температур гидродинамические потоки отсутствуют, давление постоянно и смесь газов однородна. Это означает, что соблюдаются условия
 ,
,
где n1 и n2 — концентрация частиц компонент газа; n = n1 + n2 — полная концентрация частиц.
Направим ось X системы координат в направлении градиента температур. Благодаря этому можно считать, что все величины зависят лишь от координаты х. Взяв от обеих частей уравнения состояния логарифм и продифференцировав по х, находим
 .
.
С другой стороны, из второго и третьего равенств следует, что
 .
.
Из сравнения видим, что для каждой из компонент справедливо соотношение
 .
.
Теперь воспользуемся распределением Максвелла

Обозначим Ni(vi) концентрацию молекул сорта i, скорости которых расположены вблизи скорости vi. Тогда можно записать
 ,
,
где
ni
– полная концентрация молекул. При
наличии градиента температур ni
зависит явно от координат, а
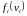 зависит от координат через температуру,
поскольку поддерживается градиент
температуры. Тогда, логарифмируя обе
части и взяв производную по х,
находим
зависит от координат через температуру,
поскольку поддерживается градиент
температуры. Тогда, логарифмируя обе
части и взяв производную по х,
находим
 ,
,
где
учтено, что
 .
Это означает, что в направлении увеличения
температуры происходит увеличение
концентрации быстрых молекул, у которых
.
Это означает, что в направлении увеличения
температуры происходит увеличение
концентрации быстрых молекул, у которых
 ,
и уменьшение концентрации медленных
молекул, у которых
,
и уменьшение концентрации медленных
молекул, у которых
 .
.
Это
рассуждение справедливо для молекул,
скорости которых расположены в окрестности
скорости vi.
Вывод формулы для диффузионного потока
(закон Фика)
 ,
где
для потока молекул предполагал, что
движение молекул прослеживалось лишь
в пределах одного свободного пробега.
На этих расстояниях скорость молекулы
постоянна. Поэтому формулу
можно записать для потока молекул
скорости vi
в виде
,
где
для потока молекул предполагал, что
движение молекул прослеживалось лишь
в пределах одного свободного пробега.
На этих расстояниях скорость молекулы
постоянна. Поэтому формулу
можно записать для потока молекул
скорости vi
в виде
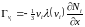 ,
,
где
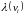 – средний свободный пробег для молекулы
со скоростью vi.
– средний свободный пробег для молекулы
со скоростью vi.
Отсюда для суммарного потока молекул сорта i получаем
 .
.
Принимая во внимание, что
 ,
,
а также равенство
,
получим выражение для потока в виде
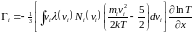 .
.
Таким образом, соотношение между направлением потока молекул и направлением, в котором растет температура, зависит от знака выражения, стоящего в квадратных скобках. Если интеграл имеет отрицательное значение. то поток направлен в сторону увеличения температуры и в области повышенной температуры концентрируется данная компонента газа. Если же интеграл положителен, поток движется против направления увеличения температуры. Следовательно, данная компонента концентрируется в более холодной области.
Заметим, что все рассмотренные нами до этого явления переноса описывали стационарные процессы. Теперь кратко рассмотрим, как можно описать нестационарные процессы.
