
- •Методические указания
- •1 Методы планирования экспериментов
- •1.1 Основные определения и понятия
- •1.2 Планирование первого порядка
- •1.2.1 Выбор основных факторов и их уровней
- •1.2.2 Планирование эксперимента
- •1.2.3 Определение коэффициентов уравнения регрессии
- •1.2.4 Статистический анализ результатов эксперимента
- •1.2.5 Дробный факторный эксперимент
- •2 Регрессионный анализ
- •2.1 Проверка адекватности модели
- •2.2 Проверка значимости коэффициентов уравнения регрессии
- •3 Пример разработки математической модели
- •4 Планирование экспериментов при поиске оптимальных условий
- •4.1 Метод крутого восхождения
- •5 Задание к выполнению курсовой работы
- •1 Методы планирования экспериментов 1
- •1.1 Основные определения и понятия 1
- •3 94026 Воронеж, Московский просп., 14
2.2 Проверка значимости коэффициентов уравнения регрессии
Надежность оценок bi уравнения регрессии можно охарактеризовать их доверительными интервалами Δbi, в которых с заданной вероятностью находится истинное значение этого параметра.
Наиболее
просто построить доверительные интервалы
для параметров линейного уравнения
регрессии, т.е. коэффициентов b0
и
b1.
При этом предполагается, что для каждого
значения случайной величины x=xi
имеется
распре-деление со средним значением
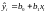 и дисперсией
и дисперсией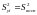 .
Иными словами, делается допущение, что
случайная величина Y распределена
нормально при каждом значении
.
Иными словами, делается допущение, что
случайная величина Y распределена
нормально при каждом значении
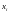 ,
а дисперсия
,
а дисперсия
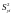 во всем интервале изменения x постоянна:
во всем интервале изменения x постоянна:
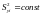 .
.
Для
линейного уравнения среднеквадратичное
отклонение i-го коэффициента уравнения
регрессии
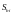 можно определить по закону накопления
ошибок.
можно определить по закону накопления
ошибок.
![]() (2.3)
(2.3)
При
условии, что
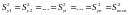 , получим
, получим
 (2.4)
(2.4)
 (2.4а)
(2.4а)
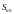 и
и
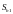 называются
соответственно стандартной ошибкой
свободного члена и стандартной ошибкой
коэффициента регрессии.
называются
соответственно стандартной ошибкой
свободного члена и стандартной ошибкой
коэффициента регрессии.
Проверка значимости коэффициентов выполняется по критерию Стьюдента. При этом проверяется нуль-гипотеза Н0: bi=0, т.е. i-й коэффициент генеральной совокупности при заданном уровне значимости α отличен от нуля.
Построим доверительный интервал для коэффициентов уравнения регрессии
![]() (2.5)
(2.5)
где число степеней свободы в критерии Стьюдента определяется по соотношению n-l. Потеря l=k+1 степеней свободы обусловлена тем, что все коэффициенты bi рассчитываются зависимо друг от друга.
Тогда доверительный интервал для Δbi коэффициента уравнения регрессии составит (bi-Δbi; bi+Δbi). Чем уже доверительный интервал, тем с большей уверенностью можно говорить о значимости этого коэффициента.
Необходимо всегда помнить рабочее правило: "Если абсолютная вели-чина коэффициента регрессии больше, чем его доверительный интервал, то этот коэффициент значим".
Таким образом, если |bi|>|Δbi|, то bi коэффициент значим, в противном случае – нет.
Незначимые коэффициенты исключаются из уравнения регрессии, а оставшиеся коэффициенты пересчитываются заново, так как они зависимы.
3 Пример разработки математической модели
В качестве примера рассмотрим разработку математической модели гидравлического режима четырехзонной методической печи с использованием теории планирования эксперимента. При планировании опытов используем методику проведения дробного факторного эксперимента (ДФЭ) первого порядка с двухуровневым варьированием факторов.
Перед разработкой плана эксперимента на основе априорной информации были выявлены факторы, влияющие на величину давления в томильной зоне печи. К числу таких факторов относятся расходы топлива на каждую зону нагрева и угол поворота дымового клапана. Расходы воздуха на каждую зону в качестве факторов не фигурировали, поскольку схема управления горением топлива автоматически меняет расход воздуха при изменении расхода газа.
О бозначим
факторы: X1
—
расход газа в томильной зоне, м3/ч;
X2
—
расход газа во второй сварочной зоне,
м3/ч;
X3
—
расход газа в первой сварочной зоне,
м3/ч;
X4
—
расход газа в нижней сварочной зоне,
м3/ч;
X5
—
положение дымового клапана, % хода
исполнительного механизма (рис.3.1).
бозначим
факторы: X1
—
расход газа в томильной зоне, м3/ч;
X2
—
расход газа во второй сварочной зоне,
м3/ч;
X3
—
расход газа в первой сварочной зоне,
м3/ч;
X4
—
расход газа в нижней сварочной зоне,
м3/ч;
X5
—
положение дымового клапана, % хода
исполнительного механизма (рис.3.1).
Рисунок 3.1 – Положение факторов (Х1, …, Х5) и отклика (Y) при проведении исследования на методической печи
Реализация ПФЭ в этом случае при варьировании всех факторов на двух уровнях потребовала бы постановки 25=32 опытов.
Будем предполагать, что эффекты взаимодействия факторов в исследуемом объекте маловероятны и пренебрежимо малы. Воспользуемся 1/4 репликой ПФЭ, т.е. ДФЭ типа 25-2, где формально 2 фактора заменены соответствующими произведениями остальных факторов (x4=x1 x2, x5=x1 x2 x3 ). Это позволит сократить число опытов до 23=8. Уровни варьирования факторов представлены в табл. 4.
Таблица 4 - Уровни варьирования факторов
Уровни факторов |
Факторы |
||||
X1, м3/ч |
X2, м3/ч |
X3, м3/ч |
X4, м3/ч |
X5, % хода ИМ |
|
Основной (нулевой) |
5250 |
3900 |
2650 |
1100 |
74 |
Нижний |
4000 |
3100 |
1750 |
700 |
50 |
Верхний |
6500 |
4700 |
3500 |
1500 |
98 |
Интервал варьирования |
1250 |
800 |
900 |
400 |
24 |
В табл. 5 приведены матрица планирования ДФЭ 25-2 и результаты эксперимента — значения выходной переменной (давления в томильной зоне методической печи).
Для обработки результатов эксперимента используем методику, изложенную ранее во втором разделе методических указаний.
1. Расчет построчных средних:
![]()
где m* — число повторных опытов (m*=2). Например,
![]()
Результаты расчета представлены в табл. 5.
Таблица 5 - Матрица ДФЭ 25-2 с двумя параллельными опытами
Факторы (кодированные значения) |
Переменная состояния (отклик), кПа |
Построчная
дисперсия
|
|||||||||||
Опыт1 |
Опыт2 |
Среднее |
Модель |
||||||||||
X0 |
X1 |
X2 |
X3 |
X4 |
X5 |
Y1 |
Y2 |
|
|
||||
1 |
1 |
1 |
1 |
1 |
1 |
-2,5 |
-2,6 |
-2,55 |
-2,41 |
0,005 |
|||
1 |
-1 |
1 |
1 |
-1 |
-1 |
2,2 |
2,3 |
2,25 |
2,26 |
0,005 |
|||
1 |
1 |
-1 |
1 |
-1 |
-1 |
5,1 |
4,7 |
4,90 |
4,74 |
0,080 |
|||
1 |
-1 |
-1 |
1 |
1 |
1 |
-1,1 |
0,5 |
-0,30 |
0,08 |
1,280 |
|||
1 |
1 |
1 |
-1 |
1 |
-1 |
2,1 |
2,3 |
2,20 |
2,26 |
0,020 |
|||
1 |
-1 |
1 |
-1 |
-1 |
1 |
-2,0 |
-2,4 |
-2,20 |
-2,41 |
0,080 |
|||
1 |
1 |
-1 |
-1 |
-1 |
1 |
0,0 |
0,8 |
0,40 |
0,08 |
0,320 |
|||
1 |
-1 |
-1 |
-1 |
1 |
-1 |
4,2 |
5,1 |
4,65 |
4,74 |
0,405 |
|||
2. Определение построчных (выборочных) дисперсий:
 Аналогично
S22=0,005;
S32=0,08;
S42=1,28;
S52=0,02;
S62=0,08;
S72=0,32;
S82=0,405.
Сумма
построчных (выборочных) дисперсий:
Аналогично
S22=0,005;
S32=0,08;
S42=1,28;
S52=0,02;
S62=0,08;
S72=0,32;
S82=0,405.
Сумма
построчных (выборочных) дисперсий:
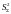 =0,005+0,005+0,08+1,28+0,02+0,08+0,32+0,405=2,195.
=0,005+0,005+0,08+1,28+0,02+0,08+0,32+0,405=2,195.
3. Определение однородности дисперсий по критерию Кохрена:
![]()
Далее
по приложению В находим
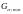 .
Для α=0,05,
m=m*-1=2-1 и
n=8 значение
.
Для α=0,05,
m=m*-1=2-1 и
n=8 значение
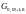 =0,6798. Поскольку
=0,6798. Поскольку
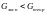 ,
то дисперсии однородны.
,
то дисперсии однородны.
4. Определение коэффициентов в уравнении регрессии:






5. Проверка значимости коэффициентов регрессии. Предварительно определим дисперсию воспроизводимости (дисперсию отклика):

Дисперсия коэффициентов уравнения регрессии
![]() Находим
значение доверительного интервала для
коэффициентов регрессии:
Находим
значение доверительного интервала для
коэффициентов регрессии:
![]()
Здесь m=n(m*-1)=8(2-1)=8, тогда теоретическое значение критерия Стьюдента t0,05;0,8=2,31 (можно рассчитать, используя функцию электронных таблиц Microsoft Excel СТЬЮДРАСПОБР(0,05;8)=2,31, откуда Δbj=2,31⋅0,131=0,303. Из сопоставления доверительного интервала Δbj с абсолютными значениями коэффициентов модели следует, что |b1|=0,069<0,303; |b3|=0,094<0,303 и |b4|=0,169<0,303. Эти коэффициенты оказались незначимы, а остальные значимы. Таким образом, окончательное уравнение регрессии запишется в виде
![]()
Результаты расчета выходных параметров по уравнению полученной модели ) занесены в табл. 5.
6. Проверка адекватности полученной модели. Предварительно определим дисперсию адекватности:

В нашем случае m*=2; n=8; l=3, и в результате имеем

С учетом ранее найденной выборочной дисперсии =2,195 определяем дисперсию воспроизводимости:
![]()
Экспериментальное значение критерия Фишера следующее:

Теоретическое
значение критерия Фишера
при α=0,05
можно
определить по приложению Б или с помощью
встроенной функции электронных таблиц
Microsoft Excel FРАСПОБР.
Для m1=(n-l)=(8-3)=5
и m2=n(m*-1)=8(2-1)=8
значение
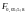 =3,69 (FРАСПОБР(0,05;5;8)=3,69).
Поскольку
=3,69 (FРАСПОБР(0,05;5;8)=3,69).
Поскольку
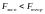 ,
то полученная модель адекватна.
,
то полученная модель адекватна.
