2.3. Типы конечных графов и их части

Если множество вершин графа конечно, то он называется конечным графом. В практических приложениях в основном имеют дело с конечными (а не бесконечными) графами. Каждое ребро графа соединяет пару вер­шин , являющихся его концами (граничными вершинами).

Для дуги орграфа различают начальную вершину, из которой дуга исходит, и конечную вершину, в которую дуга заходит. В петле гранич­ной является одна и та же вершина. Дуги и ребра с одинаковыми гранич­ными вершинами кратные. Изолированные вершины не являются концами ре­бер и не связаны ни между собой, ни с другими вершинами. Доказано, что в любом графе сумма степеней всех вершин равна удвоенному числу ребер.

Граф без петель и кратных ребер называют простым, или обыкновен­ным (рис. 2.3, а).

Граф без петель, но с кратными ребрами называют мультиграфом (рис.2.4).

Граф, в котором допускаются и петли и кратные ребра, называют псевдографом (рис. 2.5 ,а) .

Если граф не имеет ребер и все его вершины изолированы , то его называют пустым, или нуль-графом.

Простой граф, в котором любые две вершины соединены ребром, на­зывают полным (рис. 2.5, б).

Орграф считается простым, если он не имеет строго параллельных дуг и петель.

Граф, степени всех вершин которого одинаковы и равны n, назы­вается однородным (или регулярным) n-й степени (см. рис. 2.5, б).

Полный граф с n вершинами всегда однородный степени (n-1), а пустой граф - однородный степени "О". Граф третьей степени называ­ется кубическим и всегда имеет четное число вершин.

Г

Рис. 2.5. Неразделимый, полный и двудольный неориентированные графы

Если множество вершин X простого графа допускает такое разбиение на два непересекающихся подмножества X₁ и X₂ , что не существует ребер, соединяющих вершины одного и того же под­множества, такой граф называется двудольным, или биграфом (рис. 2.5, в).

Частичный граф, который наряду с некоторым подмножеством ребер графа содержит все вершины графа, называется суграфом (рис. 2.6, в).

Рис. 2.6. Подграф, частичный граф и суграф к графу рис. 2.5, а

Исходный граф по отношению к его подграфу называют надграфом, а по отношению к суграфу - сверхграфом.

Совокупность всех ребер графа (вместе с инцидентными вершинами), не принадлежащих его подграфу, образует дополнение подграфа.

Считают, что подграфы и разделены ребрами, если они не имеют общих ребер , и вершинами, если у них нет общих вершин .

Нередко задачи на графах требуют выделения различных маршрутов, обладающих определенными свойствами и характеристиками. Маршрут дли­ны определяется как последовательность К ребер графа (не обязательно различных) таких, что граничные вершины двух соседних ребер совпадают. Маршрут проходит и через все вершины, инцидентные входящим в него ребрам. Например, для графа на рис. 2.5,а маршрутами могут служить последовательности и . Первый маршрут проходит через последовательность вершин (4, 3, 2, 3, 2, 1) и соединяет вершины 4 и 1; второй - через последователь­ность вершин (2, 1, 1, 4, 1) и соединяет вершины 2 и 1.

Замкнутый маршрут приводит в ту же вершину, из которой он начался. Маршрут, все ребра которого различны, называется цепью . Маршрут, для которого различны все вершины, - простой цепью . Замкнутая цепь называется циклом , а простая цепь - простым циклом .

Цикл, который содержит все ребра графа, называется эйлеровым циклом, а граф, в котором имеется такой цикл, называется эйлеровым графом. Задача о кенигсбергских мостах сводится к выявлению сущест­вования такого цикла.

Простой цикл, который проходит через все вершины графа, назы­вается гамильтоновым.

Ориентированные маршруты на орграфе определяются аналогично с той разницей, что движение по маршруту допускается только в направ­лениях, указанных стрелками дуг.

С понятием неориентированного графа связена важная его характе­ристика, называемая связностью. Говорят, что граф связен, если любые две его вершины можно соединить цепью (см. рис.2.5, а, б). Если граф G несвязан, то его можно разбить на такие подграфы , что все вершины в каждом подграфе связны, а вершины из различных подгра­фов несвязны. Таким образом, несвязный граф представляет собой сово­купность отдельных частей (подграфов ), называемых компонентами связности графа G. Например, граф на рис.2.3, б несвязен и имеет две компоненты связности.

Если существует такая вершина связного графа, удаление которой превращает связный граф в несвязный, то она называется точкой сочленения. Ребро с такими же свойствами называется мостом (см. рис.2.3, 6). Добавив ребро (мост), соединяющее вершины 3 и 5, можно превратить компоненты несвязного графа (см. рис. 2.3, 6) в связный граф. При на­личии моста в графе имеется по крайней мере две точки сочленения. Со­вокупность компонентов несвязного графа представляет собой разбиение множеств ребер и простых циклов на непересекающиеся подмножества.

Связность ориентированных графов определяется так же, как и для неориентированных, - без учета направления дуг. Для орграфа сущест­вует понятие сильной связности. Граф сильно связан, если для любых двух вершин и существует путь, идущий из х в у.

В заключение приведем (без доказательств) ряд важнейших теорем теории графов, которые находят применение при решении практических задач.

1. Сумма степеней вершин любого графа равна удвоенному числу его ребер.

1. Число вершин нечетной степени любого графа всегда четно.

2. Во всяком графе с n вершинами (где 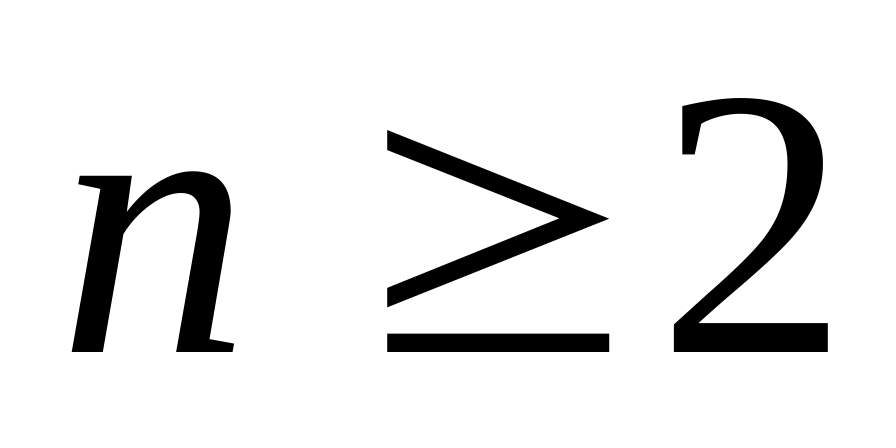) всегда найдутся две или более вершин с одинаковыми степенями.

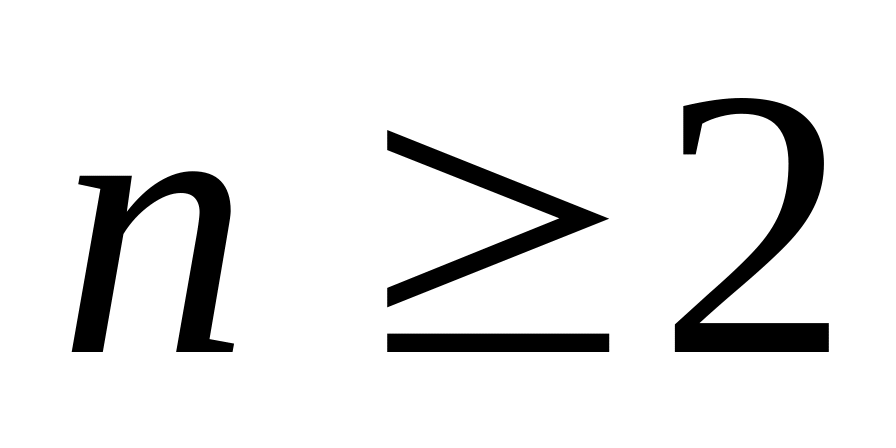3. Если в графе с n вершинами ( ) только одна пара имеет одинаковую степень, то в этом графе всегда найдется либо единственная изолированная вершина, либо единственная вершина, соединенная со всеми другими.

4. Если у графа все простые циклы четной длины, т.е. каждый цикл содержит четное число ребер, то этот граф не содержит ни одного цикла нечетной длины,

5. Для того чтобы граф был эйлеровым, необходимо и достаточно, чтобы он был связным и все его вершины имели четную степень.

6. Если данный граф является связным и имеет 2к вершин нечетной степени, то в нем можно провести К различных цепей, содержащих все его ребра в совокупности по одному разу.

2.4. Планарность графов

Граф называют планарным (или плоским), если существует изоморфный ему граф (геометрическая реализация), который может быть изображен на плоскости без пересечения ребер.

На одном из графов (рис. 2.7, а) ребра пересекаются. Два других графа (рис. 2.7, б, в), изоморфные ему, не имеют пересечений. Следовательно, граф pиc. 2.7, a, представленный другой геометрической реа­лизацией, - плоский и может быть изображен в виде рис. 2.7, г.

Рис. 2.7. Изоморфные графы

Рис.2.8. Графы Понтрягина-

Куратовского

На рис. 4.8 показаны два неплоских графа, играющие фундаментальную роль в теории планарности и называемые графами Понтрягина - Куратовского. Полный пятиугольник (рис, 2.8, а) представляет собой простой неплоский граф с минимальным числом вершин. Удаление из этого графа хотя бы одной вершины или од­ного ребра превращает его в плоский (планарный) граф.

Двудольный граф (рис. 2.8, б) - модель известной задачи о трех домах и трех колодцах: можно ли проложить от каждого из домов к каждому колодцу дороги так, чтобы они не пересекались и враждующие соседи имели возможность пользоваться всеми колодцами, но не встречаться на дорогах?

Свойства планарности не нарушаются, если некоторое ребро разбить на два введением новой вершины второй степени или заменить два ребра, инцидентные вершине второй степени, одним ребром, удалив эту вершину. Два графа называют гомоморфными (изоморфными с точностью до вер­шин второй степени), если после удаления из них вершин второй степени и объединения инцидентных этим вершинам ребер они оказываются изо­морфными (рис. 2.9). Очевидно, граф, гомоморфный плоскому графу, так­же плоский.

Доказано, что граф является плоским, когда он не содержит под­графа, гомоморфного одному из графов Понтрягина - Куратовского.

Рис. 2.9. Гомоморфные графы.

Планарность - существенное свойство графов, которые моделируют коммуникации и связи между объектами на плоскости. Например, автоматизированные транспортные связи в це­хе, дороги между населенными пунктами, водопроводные и газопроводные сети, соединения на печатных платах электронных устройств и др.