2.2. Смежность и инцидентность графов

Иногда графы удобно представлять в виде некоторых матриц, в част­ности в виде матриц смежности и инцидентности.

Вершины х и у - смежные, если они различны и если существу­ет дуга, идущая из х и у.

Обозначим вершины графа, a - его дуги. Введем числа:

Квадратная матрица порядка называется матри­цей смежности графа.

Рассмотрим граф без петель (рис. 2.4). Построим для него матрицу смежности.

u₃

Строки и столбцы этой матрицы соответствуют вершинам

гра­фа, а ее (ij )-й элемент равен чис­лу кратных дуг, направленных

от вер­шины к вершине . Дуги с одинаковыми начальными

(

Рис. 2.4. Орграф без петель

из которой дуга исходит) и конечными (в которую дуга заходит) вершинами параллельны и называется кратными.

Матрица смежности R орграфа в общем случае несимметрична, причем все элементы главной диагонали нулевые.

Любая квадратная матрица смеж­ности -го порядка может быть представлена взвешенным орграфом с вершинами, дуги которого соеди­няют смежные вершины и имеют веса, равные соответствующим элементам матрицы.

Инцидентность характеризует отношение между элементами разно­именных множеств, т.е. дуг и вершин. При рассмотрении орграфов раз­личают положительную (дуга исходит из вершины) и отрицательную (дуга заходит в вершину) инцидентности.

Дугу U называют инцидентной вершине х, если она заходит в эту вершину или исходит из нее. Введем числа:

Матрица порядка называется матрицей инциденций для дуг графа, строки которой соответствуют вершинам, а столбцы – дугам.

Для орграфа на рис. 2.4 матрице инциденций имеет вид

j = 1 2 3 4 5 6 7 8

S =

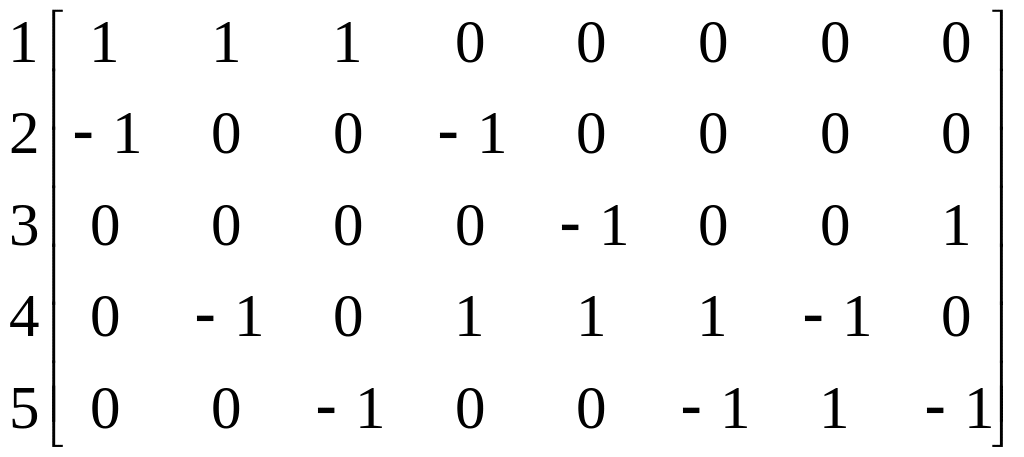
Каждый столбец матрицы инцидентности обязательно содержит два единичных элемента. Для орграфа эти элементы всегда имеют различные знаки и равны соответственно 1 и -1. Матрицы инциденций в описанном виде применимы только к графам без петель. При наличии в графе петель эту матрицу следует расчленить на две полуматрицы: положительную и отрицательную.

Неориентированный граф G можно описать заданием пары множеств (Х, U), где X - множество вершин; U - множество ребер. Более удобно описание неориентированного графа с помощью матрицы смежности или матрицы инциденций, которые строятся аналогично соответствующим матрицам для ориентированных графов с той разницей, что не делается различия между заходящей в вершину и исходящей из нее дугами. При этом вершины х и у называют смежными, если существует соединяю­щее их ребро, а само это ребро называется инцидентным вершинам х и у. Для неориентированного графа (см, рис. 2.3, а) матрицы смежности и инцидентности таковы:

j = 1 2 3 4 5 j = a b c d

R = 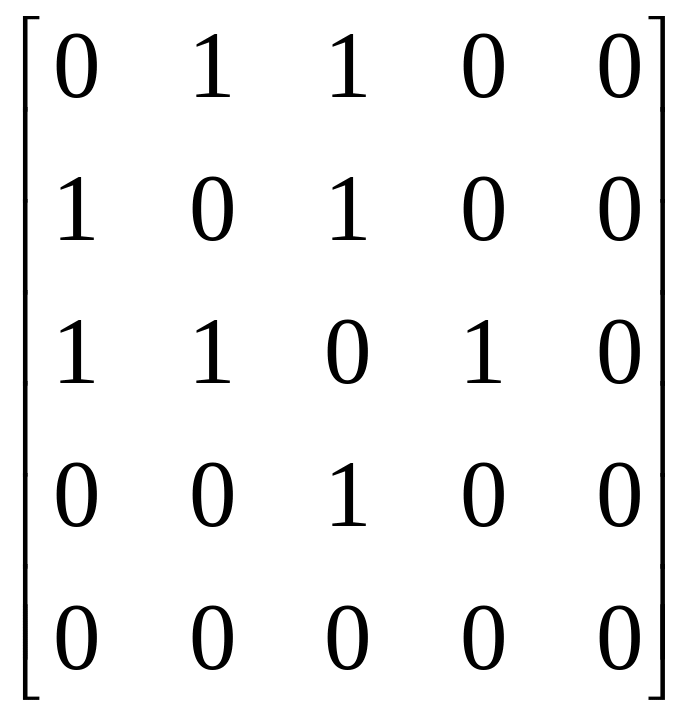S =

Матрица смежности неориентированного графа всегда симметрична. Ребрам соответствуют пары ненулевых элементов, симметричных относи­тельно главной диагонали матрицы, а петлям - ненулевые элементы глав­ной диагонали. В строках и столбцах, соответствующих изолированным вершинам, все элементы равны нулю.

Степенью вершины х, обозначаемой , называют число ребер, инцидентных вершине х.

Для графа (см. рис, 2.3, а) имеем , , , , . Если , то вершину х называют тупиковой (вершина 4). Если , то вершину называют изолированной (вер­шина 5). В каждом графе число вершин нечетной степени четно.

В матрице инцидентности каждый столбец обязательно содержит два единичных элемента. Количество единиц в строке равно степени соответствующей вершины. Нулевая строка соответствует изолированной вершине, а нулевой столбец - петле.

Графы, для которых отношения инцидентности одинаковы, являются изоморфными.