7. Поле комплексных чисел. Операции над комплексными числами в алгебраической форме записи.

Комплексным числом называется упорядоченная пара действительных чисел (a, b). Два комплексных числа (a, b) и (c, d) равны тогда и только тогда, когда a = c, b = d.

Для всех комплексных чисел C определены операции сложения и умножения по правилам:

(a, b) + (c, d) = (a + c, b + d), (a, b) · (c, d) = (ac − bd, ad + bc).

Эти операции обладают следующими свойствами:

• ассоциативность:

(a, b) + ((c, d) + (e, f)) = ((a, b) + (c, d)) + (e, f),

(a, b) · ((c, d) · (e, f)) = ((a, b) · (c, d)) · (e, f);

• коммутативность:

(a, b) + (c, d) = (c, d) + (a, b), (a, b) · (c, d) = (c, d) · (a, b);

• дистрибутивность:

(a, b) · ((c, d) + (e, f)) = (a, b) · (c, d) + (a, b) · (e, f).

Деление. Производится с домножением на сопряженное.

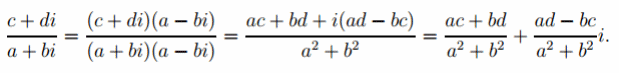
Обычно комплексное число обозначают одной буквой, например: z = a + bi, здесь a называется действительной частью числа z, b — мнимой частью.

Комплексные числа нельзя сравнивать!

8. Тригонометрическая форма записи и геометрическая интерпретация комплексных чисел. Умножение и деление комплексных чисел в тригонометрической записи. Формула Муавра.

Пусть на плоскости задана прямоугольная система координат. Тогда произвольному компл. ч. (a, b)=a+bi можно сопоставить точку с координатами (a, b). Заданная пл. называется комплексной. Ось абсцисс (действительная ось Re) будет соответствовать мн. действительных чисел. Ось ординат (мнимая ось Im) - множеству чисто мнимых чисел.

Модулем, или абсолютной величиной, комплексного числа называется расстояние r точки z до начала координат (|z|). Аргументом числа z назовем угол ϕ, отсчитываемый в положительном направлении (против ч. стр.), между направлением оси Re и радиус-вектором точки z.

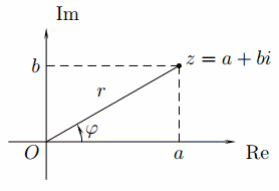
Арумент (arg z) определен с точностью до 2πk. Применяя теорему Пифагора и формулы тригонометрии:|a + bi| =√a² + b², a = r cos ϕ, b = r sin ϕ,откуда a + bi = r(cos ϕ + isin ϕ). Это тригонометрическая форма записи

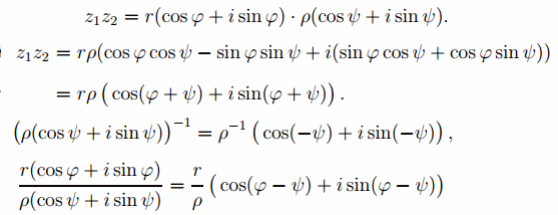
Формала Муавра:

9. Извлечение корня натуральной степени из комплексных чисел.

Пусть n ∈ N. Число z называется значением корня n-й степени из числа ζ(зэта), если zⁿ = ζ.Легко видеть, что ζ = 0 обладает единственным (нулевым) значением корня произвольной натуральной степени.

Пусть ζ <> 0, тогда, очевидно, z <>0. Представим ζ в тригонометрической форме: ζ = ρ(cos ψ + isin ψ). Мы ищем такое z =r(cos ϕ + isin ϕ), что zⁿ = ζ. Воспользовавшись формулами Муавра, последнее равенство перепишем в виде rⁿ=cos(nϕ) + isin(nϕ)= ρ(cos ψ + isin ψ).

Так как для ненулевого комплексного числа модуль определен однозначно, а аргумент с точностью до 2πk, где k ∈ Z, то {rⁿ = ρ, а nϕ = ψ + 2πk} Получаем:r =ⁿ√ ρ, ϕ =(ψ + 2πk)/n (для вычисления r используется арифметическое значение корня ⁿ √ ρ). Итак, для произвольного k ∈ Z каждое из чисел z =ⁿ√ ρ (cos(ψ + 2πk)/n+ isin(ψ + 2πk)/n) является значением корня n-й степени из числа ζ = ρ(cos ψ + isin ψ).

Выясним, есть ли среди чисел совпадающие. Разделим произвольное k ∈ Z на n с остатком, т. е. представим k в виде k = np + q. Подставляя это выражение для k получаем:

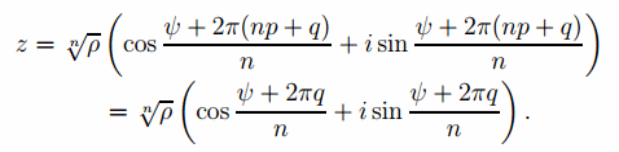
С другой стороны, при значениях k = 0, 1, . . . , n−1 все числа различны: их аргументы различны и отличаются не более, чем на 2π.

Точки комплексной плоскости, соответствующие всем значениям корня степени n ≥ 3 из одного и того же числа, находятся в вершинах правильного n-угольника.