1. Нод целых чисел. Алгоритм Евклида.
Если некоторое целое число d является делителем одновременно для каждого из двух заданных чисел a и b, то d называется их общим делителем. Среди всех общих делителей двух заданных целых чисел a и b выберем максимальный. Он называется наибольшим общим делителем этих чисел и обозначается НОД(a, b).
Алгоритм Евклида: пусть a и b - целые числа, не равные нулю. Тогда последовательность чисел a>b>r1>...>rn определена тем, что каждое rk - это остаток от деления предпредыдущего на предыдущее число, а предпоследнее делится на последнее нацело. Последний не нулевой член этой последовательности - НОД.
Теорема. Для любых целых чисел a и b, не равных нулю, алг. Евк. останавливается за конечное число шагов и корректно вычисляет НОД {a, b}.
Док-во: 1) По свойству операции деления с остатком (остаток не меньше нуля и строго меньше модуля делителя) имеем: |b| < r1 < r2 < r3 < . . . ≤ 0 - ч. и т.д.
2) См. алгоритм. rs-1:d (1). qs :d и rs :d => rs-2:d(2). Из (1) и (2): rs-3:d и т.д. В конце получаем: r2 :d, r1:d, b:d, a:d. d - общий делитель. Тогда пусть δ - произвольный общий делитель. Докажем, что если d делится на δ, т.е. на любой общий делитель, то он больший.
b:δ , a:δ => r1=a-q1b:δ, r2=b-q2r1:δ, ..., rs=rs-2-qsrs-1:δ ч. и т.д.
2. Расширенный алгоритм Евклида. Коэффициенты Безу (линейное разложение нод)
Теорема о линейном разложении НОД: Пусть a, b — целые числа, одновременно не равные нулю, и d= НОД(a, b). Тогда найдутся такие целые u, v, что ua + vb = d.
Числа u и v называются коэффициентами Безу.
Док-во: Применим к a и b алгоритм Евклида. В ходе его работы получим последовательности частных q1, q2, . . . , qs+1 и остатков r1, r2, . . . , rs. На первой итерации запишем два тривиальных равенства: a = 1·a + 0·b, b = 0·a + 1·b. Вычтем из первого второе, умноженное на q1. Тогда согласно в левой части получим r1 (из алг. Евклида). В правой части соберем множители у a и у b: r1 = 1·a + (−q1)�b. На второй итерации вычтем из равенства 2 равенство 3, умноженное на q2. Согласно алг. в левой части получим r2. В правой части снова соберем множители у a и у b: r2 = (−q2)·a + (1 + q1q2)·b.
На третьей итерации получим r3 = (1 + q2q3)·a + (−q1 − q3 − q1q2q3)�b. Будем выполнять такие преобразования далее. На k-й итерации (k = 1, 2, . . . , s) получим: rk = uka + vkb. На s-й итерации получим: d = rs = usa + vsb. Ч. и т.д..
Алгоритм нахождения коэффициентов Безу, описанный при док-ве теоремы - расширенный алгоритм Евклида.
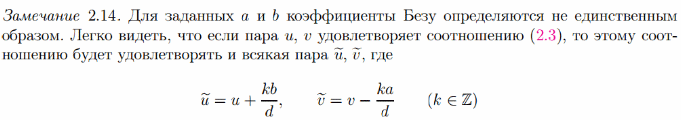
3. Взаимно простые числа. Критерий взаимно простых чисел. Свойства взаимно простых чисел.
Два целых ненулевых числа a и b называются взаимно простыми, если НОД(a, b) = 1 или единственными общими делителями чисел a и b являются числа ±1.
Критерий: Для того, чтобы целые числа a и b были взаимно простыми, необходимо и достаточно, чтобы существовали такие целые числа u и v, что ua + vb = 1.
Док-во: Необходимость следует из теоремы о линейном разложении НОДа. Достаточность. Пусть выполнено ua + vb = 1 и δ — произвольный общий делитель чисел a и b. Очевидно, что левая часть равенства делится на δ, но тогда делится и правая часть, т.е. 1:δ, откуда δ = ±1. А значит a и b - взаимно простые. Св-ва вз. пр. чисел:
1) Если число a взаимно просто с каждым из чисел b и c, то оно взаимно просто и с их произведением bc.
Док-во:Так как число a взаимно просто с каждым из чисел b и c, то найдутся такие u1, u2, v1, v2, что u1a+v1b=1, u2a+v2c=1.
Складывая эти два равенства и осуществляя преобразования, получаем: (u1u2a + u1v2c + v1bu2)a + (vv1)bc = 1. Значит по критерию вз.пр. чисел - числа a и bc взаимно просты.
2) Если ab:c, причем a и c взаимно просты, то b:c.
Док-во. Так как a и c взаимно просты, то по критерию найдутся такие u, v, что ua + vc = 1. Умножая обе части этого равенства на b, получаем uab + vcb = b. Очевидно, второе слагаемое в левой части делится на c. Первое слагаемое левой части делится на c по условию. Следовательно, b:c.
3)Если a:b и a:c, причем b и c взаимно просты, то a:bc.
Док-во. Так как a:b, то для некоторого q имеем a = qb. Но a:c. Так как b и c взаимно просты, то по 2 св-ву b:c, откуда a:bc.