Задача о максимальном потоке в сети.

Задача о максимальном потоке заключается в поиске таких потоков по дугам, принадлежащих множеству E, когда результирующий поток, протекающий из источника s в сток t, является максимальным. Эта задача важна и сама по себе и имеет многочисленные приложения, в том числе для решения транспортной задачи.

Обозначим через d интенсивность источника, которую считаем неизвестной. Очевидно, интенсивность стока равна –d. Значение d , при котором сеть допускает поток , называется величиной потока из источника в сток. Требуется найти максимальное значение d, при котором сеть допускает поток.

Максимальное значение d называется величиной максимального потока из источника в сток.

С понятием потока в сети связано понятие величины разреза сети. Допустим, что множество всех вершин данной сети разбито на два взаимно дополнительных подмножества D_s и D_t, причем первое подмножество содержит вход s € D_s, а второе — выход сети t € D_t; сумма двух подмножеств D_s и D_t составляет множество всех вершин сети. В этом случае говорят, что в сети произведен разрез. Множество дуг (i, /), где i € D_s, / € D_t, называется разрезом.

Сумма пропускных способностей дуг разреза называется величиной разреза

Разрез, имеющий наименьшую пропускную способность, называется минимальным

В общем случае величина потока на конечных дугах никогда не превышает величину любого разреза .

Фордом и Фолкерсоном доказана фундаментальная теорема , имеющая большое значение в теории графов.

ТЕОРЕМА . Для любой сети максимальная величина потока из s в t равна минимальной пропускной способности разреза, отделяющего s и t.

Положим интенсивность источника , равной достаточно большому числу d, а интенсивность стока – d, для полученной сети рассмотрим задачу об оптимальном потоке при функции стоимости :

(5)

Следовательно, рассмотрим задачу минимизации X_st при условия

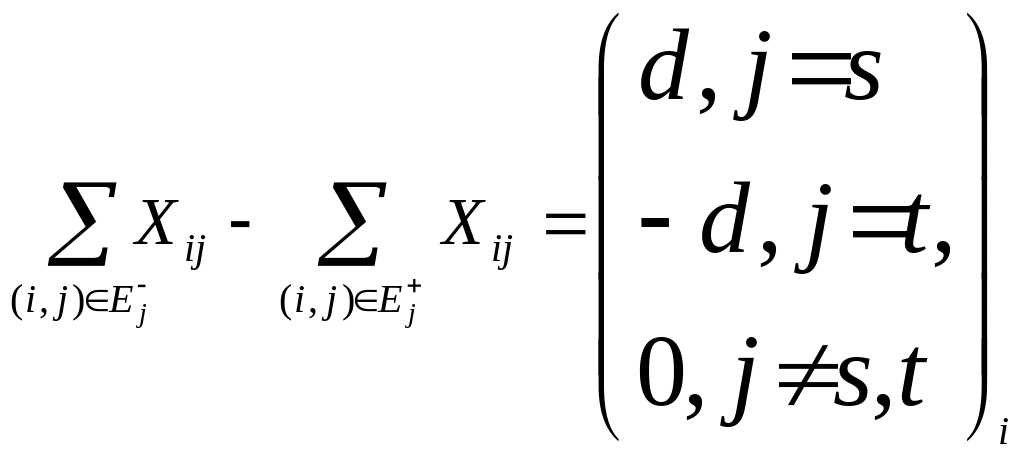(6)

для всіх дуг ; (7)

Очевидно, если X_st будет наименьшим, то через остальные дуги сети пройдет наибольшее количество потока. Поэтому такая задача соответствует задаче о максимальном потоке.

3. Змістовна постановка задачі

Задані: топологічна структура мережі, пропускна здатність каналів зв’язку. Використовуючи математичну модель задачі про максимального потоку за допомогою програмного середовища MatLab з використанням інструментарію «Optimization Toolbox», побудувати мережу з максимальним потоком. (Варіант завдання одержати у викладача).

9. Опис лабораторної установки

Лабораторна робота виконується на ПЕОМ у програмному середовищі MatLab з використанням інструментарію «Optimization Toolbox». У вказаний інструментарій входить функція «linprog», що дозволяє знаходити оптимальне рішення задачі лінійного програмування, яку задано в наступному вигляді:

при ; ;

де , , , , і – вектори, і – матриці.

Синтаксис команд:

x = linprog (f, [], [], Aeq, beq) – знаходження значення вектора при .

X = linprog (f, A, b, [], []) – знаходження значення вектора при .

X = linprog (f, A, b, Aeq, beq) – знаходження значення вектора при ; .

X = linprog (f, A, b, Aeq, beq, lb, ub) – знаходження значення вектора при ; ; .

[x,fval] = linprog(…) – знаходження значень вектора і , параметри функції linprog можуть бути задані одним із вказаних вище способів.

Пример..Задача об максимального потока в сети (рис.3.1)

Рис. 3.1

>> f = [0;0;0;0;0;0;0;0;0;1];

Aeq = [ 1 1 0 0 0 0 0 0 0 1

-1 0 1 1 0 0 0 0 1 0;

0 -1 0 -1 1 0 0 0 0 0;

0 0 -1 0 0 -1 0 1 0 0 ;

0 0 0 0 -1 1 1 0 -1 0

0 0 0 0 0 0 1 1 0 1 ];

beq = [10000;0;0;0;0; 10000 ];

lb = zeros(10,1);ub=[4;5;1;2;3;2;6;2;4;1000000]

[x,fval] = linprog(f,[],[],Aeq,beq,lb,ub);

x

fval

Optimization terminated successfully.

X =

1.0e+003 *

0.0040

0.0030

0.0009

0.0000

0.0030

0.0007

0.0053

0.0017

0.0031

9.9930

fval = 9.9930e+003

3.5 Порядок виконання роботи і методичні вказівки з її виконання

3.5.1 Відповідно до умови й вихідних даних свого завдання записати 35математичну постановку задачі про максимальний потік у вигляді задачі лінійного програмування . Сформувати вектори , , , , і ; матриці й .

3.5.2 Запустити пакет MatLab. У вікні редагування М-файлів (М-file Editor) набрати текст програми й записати її під ім’ям, що відповідає номеру групи й номеру отриманого варіанта, наприклад: 04_1_5.

3.5.3 Одержати оптимальне рішення, виконавши створену програму.

3.5.4 Проаналізувати отримані результати.

4. Зміст звіту

Звіт повинен містити:

• змістовну постановку задачі;

• математичну постановку задачі ЛП для свого варіанта;

• текст програми;

• результати виконання програми;

• виводи по роботі.

3.7 Зміст звіту

Звіт повинен містити:

• змістовну постановку задачі;

• математичну постановку задачі для свого варіанта;

• вихідні дані програми;

• результати виконання програми;

• висновки з роботи.

3.8 Контрольні запитання і завдання

1. У чому полягає задача про максимальний потік?

2. Як визначається розріз у мережі?

3. Сформулюйте теорему Форда і Фалкерсона.

4. Викладіть алгоритм Форда і Фалкерсона.

5. Сформулюйте метод приєднаної мережі.

6. Сформулюйте метод максимального потоку мінімальної вартості.

6. Сформулюйте математичну постановку задачі про оптимальний потік в мережі.

7. Наведіть визначення максимального потоку в мережі .

8. Сформулюйте математичну постановку задачі про найкоротший шлях в мережі, приведить приклад ії використання в сфері телекомунікацій.

9 . Сформулюйте математичну постановку задачі про максимальний потік.

11. Приведить приклад використання потокових моделей в сфері телекомунікацій.

ЛАБОРАТОРНА РОБОТА 4

ВИКОРИСТАННЯ БАГАТОКРИТЕРІАЛЬНОЇ ОПТИМІЗАЦІЇ

ДЛЯ ВИБОРУ РАЦІОНАЛЬНОЇ СТРУКТУРИ СИСТЕМИ ЗВ’ЯЗКУ.

4.1Мета роботи

1. Одержати практичні навички у використанні методу багатокритеріальної оптимізації при вирішенні задач вибору раціональної структури мережі зв’язку.

2. Закріпити навички роботи з ЕОМ.

4.2 Методичні вказівки до самостійної роботи студентів

4.2.1 Підготовка до лабораторної роботи

Студент повинен вивчити теоретичний матеріал по темі «Методи прийняття рішень» за конспектом лекцій і навчальною літературою [4,5,6].

При підготовці до виконання лабораторної роботи необхідно:

знати: визначення задачі багатокритеріальної оптимізації, поняття приватного й узагальненого критеріїв, структуру алгоритму програми, що використовується в лабораторній роботі, та особливості її використання, структуру вхідних даних.

Уміти: маючи змістовну постановку задачі сформувати набір приватних критеріїв і визначити множину варіантів можливих структур мережі зв’язку.

Підготувати: вихідні дані для кожного із трьох випадків наявності апріорної інформації, бланк звіту, усні відповіді на контрольні запитання.