Розрахувати значення коефіцієнтів .
Для розрахунку коефіцієнтів на трасах БС-ЛА за відсутності перешкод в межах прямої видимості можна скористатися наступною емпіричною формулою [7]:
,
(1.10)
де
–
частота
несучої при передачі;
– відстань
між передаючою і приймальною антенами.
Для розрахунку коефіцієнтів загасання на трасах РСБН-МС в межах міської зони можна скористатися емпіричною формулою Окомури, що міститься в рекомендації Р.370 ITU-R:
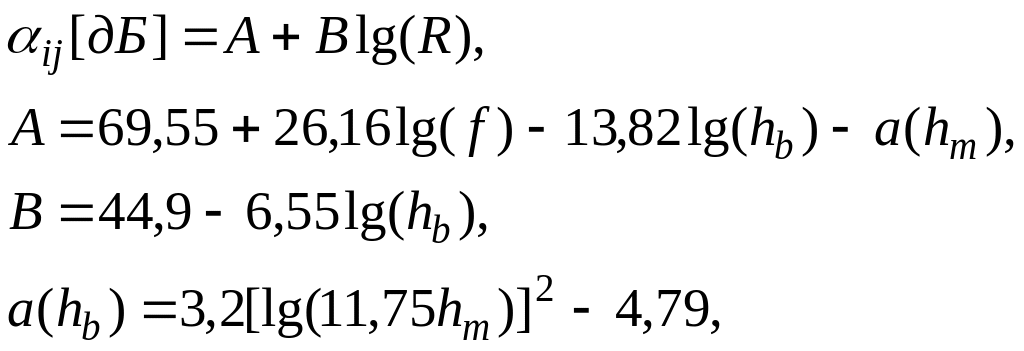(1.11)
де
– висота розміщення антени БС,
– висота
розміщення антени Мс.
При
розрахунках можна прийняти
м,
м.
Значення коефіцієнтів необхідно перетворити до необхідного вигляду по формулі:
,
(1.12)
Розраховуємо потужність шумів природного походження:
,
(1.13)
де – коефіцієнт шуму приймача, 7-10 дБВт;
Вт/Гц·град
– постоянная Больцмана;
К;
– смуга
частот,
0.8 МГц.
Визначити мінімальні значення потужностей всіх передавачів угруповання, використовуючи процедуру linprog Matlab. Як мінімально припустиме відношення перешкода/сигнал вибрати значення
з табл.1.2.
Опис лабораторної установки
Лабораторна робота виконується на ПЕОМ у програмному середовищі MatLab 6.5 з використанням інструментарію «Optimization Toolbox». У вказаний інструментарій входить функція «linprog», що дозволяє знаходити оптимальне рішення задачі лінійного програмування, яку задано в наступному вигляді:
при
;
;
де
,
,
,
,
і
– вектори,
і
– матриці.
Синтаксис команд:
x = linprog (f, [], [], Aeq, beq) – знаходження значення вектора при .
x = linprog (f, A, b, [], []) – знаходження значення вектора при .
x = linprog (f, A, b, Aeq, beq) – знаходження значення вектора при ; .
x = linprog (f, A, b, Aeq, beq, lb, ub) – знаходження значення вектора при ; ; .
[x,fval]
= linprog(...) – знаходження значень вектора
і
, параметри функції linprog можуть бути
задані одним із вказаних вище способів.
Таблиця 1.2.
№ варіанта |
, дБ |
R1, км |
R2, км |
R3, км |
R4, км |
R5, км |
R6, км |
R7, км |
1 |
-10 |
30 |
15 |
20 |
40 |
2,1 |
1,5 |
3,0 |
2 |
-11 |
30 |
15 |
20 |
40 |
2,2 |
1,6 |
3,9 |
3 |
-9 |
30 |
15 |
25 |
40 |
2,3 |
1,7 |
3,8 |
4 |
-12 |
30 |
15 |
20 |
40 |
2,4 |
1,8 |
3,7 |
5 |
-10 |
35 |
18 |
20 |
43 |
2,5 |
1,9 |
3,6 |
6 |
-11 |
35 |
20 |
23 |
45 |
2,6 |
1,0 |
3,5 |
7 |
-9 |
35 |
20 |
28 |
35 |
2,7 |
1,1 |
3,4 |
8 |
-10 |
32 |
20 |
27 |
42 |
2,8 |
1,2 |
3,3 |
9 |
-11 |
37 |
20 |
25 |
40 |
2,9 |
1,3 |
3,2 |
10 |
-12 |
35 |
20 |
22 |
38 |
2,0 |
1,4 |
3,1 |
11 |
-9 |
32 |
20 |
20 |
39 |
2,1 |
1,5 |
3,0 |
12 |
-9 |
34 |
20 |
20 |
39 |
2,2 |
1,6 |
3,9 |
13 |
-11 |
29 |
20 |
20 |
39 |
2,3 |
1,7 |
3,8 |
14 |
-10 |
28 |
20 |
20 |
39 |
2,4 |
1,8 |
3,7 |
15 |
-11 |
34 |
20 |
18 |
38 |
2,5 |
1,9 |
3,6 |
16 |
-9 |
34 |
23 |
18 |
41 |
2,6 |
1,0 |
3,5 |
17 |
-12 |
37 |
25 |
19 |
42 |
2,7 |
1,2 |
3,4 |
18 |
-11 |
30 |
24 |
19 |
42 |
2,8 |
1,3 |
3,3 |
19 |
-10 |
26 |
21 |
18 |
40 |
2,9 |
1,4 |
3,2 |
20 |
-10 |
38 |
23 |
19 |
40 |
2,0 |
1,5 |
3,1 |
Текст (лістинг) програми набирається у вікні редагування М-файлів – М-file Editor.