МIНIСТЕРСТВО ОСВIТИ І НАУКИ УКРАЇНИ

ХАРКIВСЬКИЙ НАЦІОНАЛЬНИЙ

УНIВЕРСИТЕТ РАДIОЕЛЕКТРОНIКИ

Методичні вказівки

до лабораторних робіт

з дисципліни

«Управління та оптимізація в ТКС»

для студентів усіх форми навчання

напряму 6.050903 „Телекомунікації”

Електронне видання

Затверджено

кафедрою «Телекомунікаційні системи».

Протокол № від 2014 р.

ХАРКIВ 2014

Методичні вказівки до лабораторних робіт з дисципліни «Управління та оптимізація в ТКС» для студентів усіх форм навчання напряму 6.050903 „Телекомунікації” [Електронне видання] / Упоряд. Л. І. Мельнікова, Т.М. Коваленко, Є.В. Кузміних, – Харків: ХНУРЕ, 2014. – 45 с.

Упорядники: Мельнікова Любов Іванівна

Коваленко Тетяна Миколаївна

Кузміних Євгенія Володимирівна

Рецензент: О.Ю. Євсєєва, д-р. техн. наук, проф. каф. ТКС

ВСТУП

При розв’язанні задач синтезу структури та вибору параметрів телекомунікаційних систем, а також задач оптимального управління ними найчастіше їх можна звести до виду знаходження значень низки параметрів так, щоб досягався екстремум деякої функції якості рішення, при деякому набору обмежень. Деяка група з цих задач, таки як задачі маршрутизації, вибору топології та ін., можна розв’язати зі застосування апарату теорії графів. Інші задачі, таки як задача вибору пропускної здібності каналів зв’язку та інші, можуть бути зведені до класичних задач оптимізації таких як: задача лінійного програмування, транспортної задачі, нелінійного програмування і т.п.

Дисципліна «Управління та оптимізація в ТКС» забезпечує вивчення методів оптимізації та освоєння основ теорії управління з позиції їх практичного застосування в телекомунікаційних системах (ТКС).

За результатом вивчення дисципліни студенти повинні вміти в процесі аналізу і синтезу телекомунікаційної системи і її елементів виділяти основні структурні і функціональні параметри;і формулювати змістовну постановку задачі оптимізації; приводити її до однієї з відомих математичних моделей; аргументовано обгрунтовувати вибір методу рішення; отримувати якісне рішення з використанням пакету MATLAB; інтерпретувати рішення у рамках змістовної постановки.

В методичних вказівках до лабораторних робіт приведено 5 лабораторных работ, в яких реалізовані основні численные методи рішення оптимизаційних задач, а також дані практичні рекомендації по використанню пакету MATLAB при виконанні лабораторних робіт.

ЛАБОРАТОРНА РОБОТА 1

ОПТИМАЛЬНЕ УПРАВЛІННЯ РЕСУРСАМИ ЗВ'ЯЗКУ

З РУХОМИМИ ОБ'ЄКТАМИ НА ЗАДАНІЙ ТЕРИТОРІЇ

1. Мета роботи

1. Одержати практичні навички з використання алгоритму оптимізації на базі симплекса-методу рішення задач лінійного програмування в техніці зв'язку.

2. Закріпити навички роботи з ЕОМ.

2. Методичні вказівки до самостійної роботи студентів

1. Підготовка до лабораторної роботи

При підготовці до лабораторної роботи студент повинен вивчити теоретичний матеріал по темі «Методи лінійного програмування» по конспекту лекцій і навчальній літературі [1,2,3,4].

При підготовці до виконання лабораторної роботи необхідно:

знати: математичну постановку задачі лінійного програмування та її геометричну інтерпретацію, алгоритм симплекс-методу й особливості його використання;

уміти: маючи змістовну постановку задачі сформулювати її математичну постановку у вигляді задачі ЛП у стандартному й канонічному вигляді, визначити вихідне базисне рішення, графічно досліджувати задачу на наявність рішення.

підготувати: математичний запис задачі лінійного програмування для свого варіанта завдання в стандартному й канонічному вигляді (номер варіанта задається викладачем), графічне дослідження задачі на наявність рішення, бланк звіту, усні відповіді на контрольні запитання.

2. Загальні відомості з теорії оптимізації та методів лінійного програмування

Задача лінійного програмування, записана в канонічній формі, полягає в наступному. Задано систему лінійних рівнянь із невідомими:

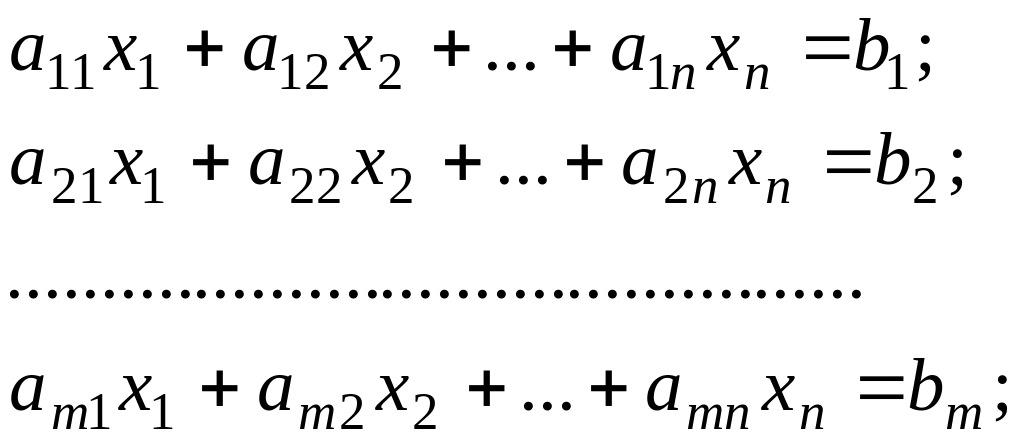(1.1)

і лінійну функція щодо змінних

. (1.2)

Потрібно знайти такі ненегативні значення змінних , які задовольняли б системі рівнянь (1.1) і, крім того, перетворювали в максимум лінійну функцію (1.2)

Якщо за умовами задачі потрібно відшукати мінімум функції , записаної у вигляді (1.2), то задачу можна звести до задачі максимізації функції

. (1.3)

Максимум функції (1.3) і мінімум функції (1.2) будуть досягатися при тому самому наборі змінних ( ).

Лінійну функцію виду (1.2) прийнято називати лінійною формою задачі, а безліч наборів ( ), що задовольняють умовам ненегативності змінних і рівнянням (1.1), – областю визначення задачі.

Припустимим рішенням основної задачі ЛП будемо називати будь-яку сукупність змінних

, (1.4)

що задовольняє рівнянням (1.1).

Оптимальним рішенням будемо називати те із припустимих рішень, для якого лінійна форма обертається в максимум ( обертається в мінімум).

Якщо число невідомих параметрів менше числа обмежень, то задача ЛП не має рішень, таким чином, не можна знайти набір невідомих, що задовольняє системі з рівнянь при . Для випадку система (1.1) буде мати єдине рішення, якщо її визначник не дорівнює нулю. Функція при цьому здобуває цілком певне єдине значення, і задача оптимізації втрачає сенс. Але при можна знайти безліч рішень, що задовольняють обмеженням (1.1) і (1.4). У цьому випадку й виникає задача ЛП по знаходженню оптимального рішення.

3. Симплекс-метод рішення задач лінійного програмування

Симплекс-метод можна застосовувати для вирішення будь-якої задачі ЛП. З геометричного змісту задачі лінійного програмування випливає, що для її вирішення необхідно обчислити координати всіх вершин багатогранника області припустимих рішень, утвореного обмеженнями, і значення лінійної форми в них. Перебором всіх вершин можна знайти таку вершину, де функція здобуває екстремальне значення. При цьому можливі такі труднощі:

• оскільки , то система обмежень лінійно залежна і для побудови багатокутника рішень необхідно виділити всі лінійно незалежні системи рівнянь і їх рішення;

• число вершин багатогранника різко зростає зі збільшенням 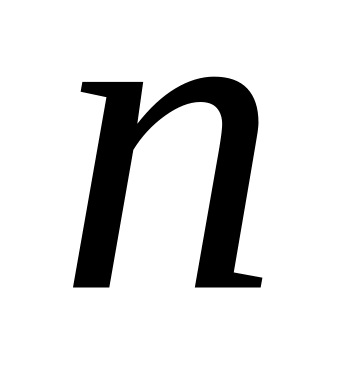і і такий метод перебору всіх вершин може виявитися занадто трудомістким.

Симплекс-метод забезпечує більш раціональне рішення, ніж метод прямого перебору. Його суть полягає в тому, що відправляючись із деякої довільної вершини багатогранника обмежень, переходять до обчислення тільки такої вершини, у якій значення лінійної форми буде більше, ніж у попередній. Інші варіанти не обчислюються. Тоді при кінцевому порівняно малому числі кроків може бути знайдений оптимальний план. Таким чином, виробляється впорядкований перебір вершин, при якому відбувається постійне збільшення лінійної форми.

Тому симплекс-метод називають також методом послідовного поліпшення плану.

Знаходження рішення задачі симплексом-методом містить у собі два етапи. Перший складається в знаходженні однієї довільної вершини багатогранника обмежень, координати якого визначає початковий опорний план (вихідне базисне рішення). Другий етап складається в послідовному впорядкованому переході від однієї вершини багатогранника до іншої, суміжної з нею. Оскільки прилягаючих вершин багато, щораз вибирається така вершина, при переході до якої забезпечується найбільше зростання лінійної форми. На кожному кроці процесу поліпшення плану виконується перевірка на оптимальність. Очевидно, що план буде оптимальним, якщо серед вершин, що прилягають до даної, немає такої, при переході до якої відбувається зростання лінійної форми.

4. Визначення вихідного базисного рішення

При виборі вихідного базисного рішення розглянутим вище способом варто розрізняти три випадки.

1. Система обмежень задана у вигляді нерівностей, тобто

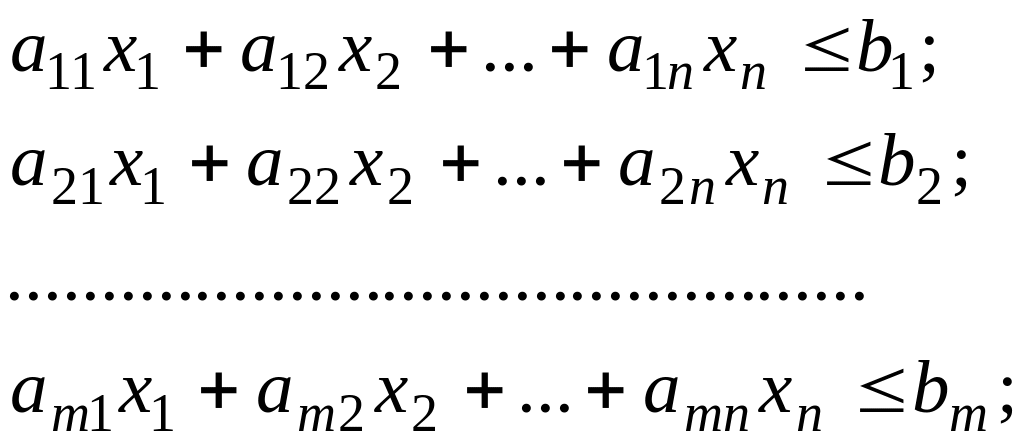(1.5)

Щоб перейти від нерівностей до рівностей, уведемо додаткові невідомі , які в лінійну форму задачі входять із нульовими коефіцієнтами, а в систему обмежень – з коефіцієнтами, рівними одиниці. Тоді система (1.5) матиме наступний вигляд:

(1.6)

Для зручності подальших міркувань запишемо коефіцієнти системи при однакових невідомих (по стовпцях) у вигляді наступних векторів:

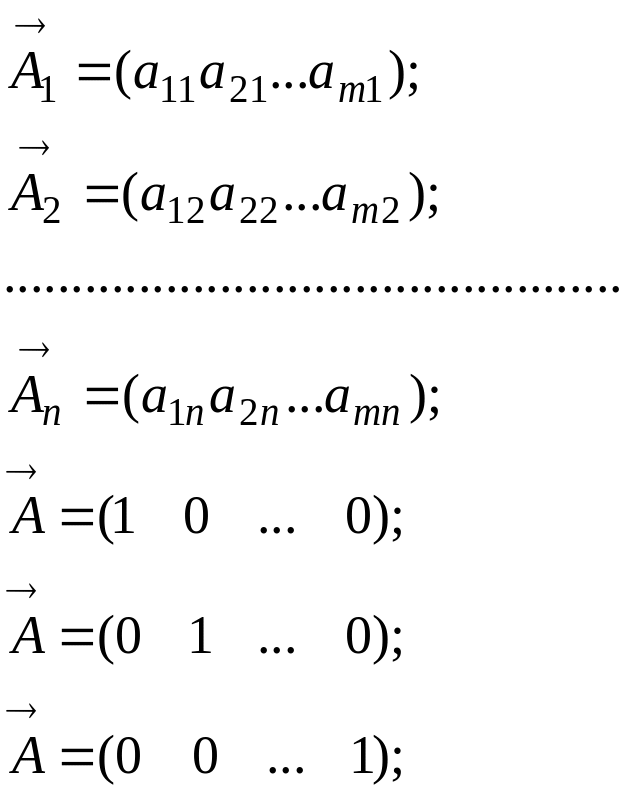
Система обмежень у векторній формі приймає вигляд

. (1.7)

Вектор є -мірними, а їхнє число дорівнює , але оскільки , вони лінійно залежні. Координати однієї з вершин багатогранника обмежень можуть бути утворені системою з лінійно незалежних векторів. Таку систему називають базисом задачі. Відомо, що для знаходження базису необхідно виділити ту частину системи (1.6), для якої визначник матриці, складеної з коефіцієнтів системи, відмінний від нуля. У системі (1.6) це виконується для матриці коефіцієнтів при додаткових невідомих, котра є одиничною і її визначник не дорівнює нулю:

Отже, вектори , лінійно незалежні. Координати вершини, що утворить даний базис, легко одержати, прийнявши й розв’язавши виділену із системи (1.6) систему лінійно залежних рівнянь:

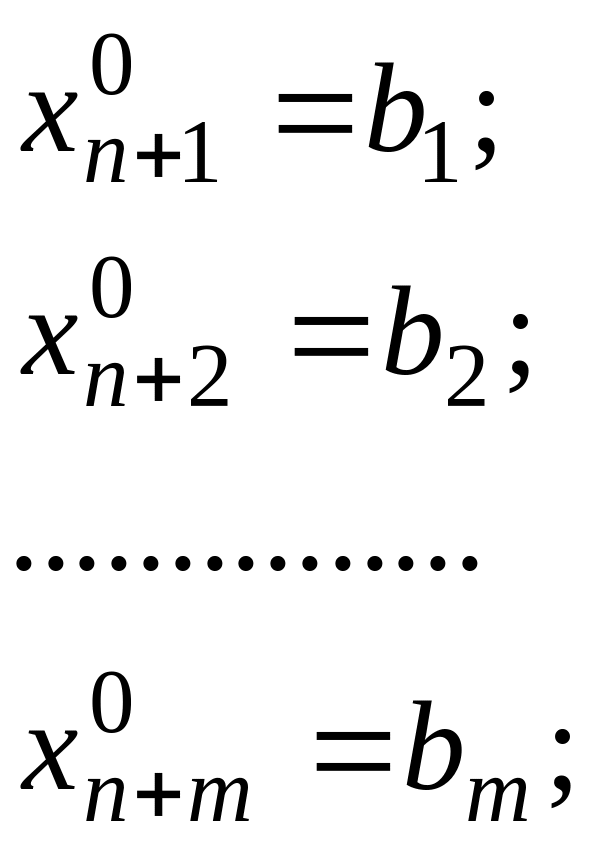
Отже, початковий опорний план є

Таким чином, шляхом введення додаткових невідомих ми знаходимо координати початкової вершини, тобто звільняємося від необхідності відшукувати системи лінійно незалежних векторів серед безлічі й розв’язувати системи рівнянь для них.

Очевидно, що розширення задачі за рахунок додаткових змінних збільшує число вершин багатогранника обмежень і число кроків у процесі послідовного впорядкованого перебору вершин у напрямку зростання лінійної форми. Ця обставина веде до збільшення часу другого етапу, але виграш на першому етапі компенсує його.