3. Расчет быстроходной внутренней конической передачи

3.1 Выбор твёрдости, термообработки и материала колёс быстроходной зубчатой передачи

Выберем материал для зубчатой пары колёс, одинаковый для шестерни и колеса, но с разными твёрдостями, так как твёрдость зубьев шестерни должна быть больше твёрдости зубьев колеса

Принимаем для шестерни – Сталь 45 и для колеса - Сталь 40 [4]. Выберем термообработку для зубьев шестерни и для зубьев колеса - улучшение.

Выберем интервал твёрдости зубьев шестерни HB₁ = 235…262 HB и колеса HB₂ = 192…228 HB.

Определяем среднюю твёрдость зубьев шестерни HB_1ср и колеса HB_2ср

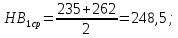
Определяем разность средних твёрдостей зубьев шестерни и колеса

При этом соблюдается необходимая разность средних твёрдостей зубьев шестерни и колеса.

Определяем механические характеристики сталей для шестерни и колеса:

- для шестерни

- для колеса

По таблице 3.2 [4] выбираем предельные значения размеров заготовки шестерни (D_пред - диаметр) и колеса (S_пред - толщина обода или диска):

- для шестерни D_пред = 125 мм,

- для колеса S_пред = 60 мм.

Определяем допускаемые контактные напряжения .

Определяем коэффициент долговечности для зубьев шестерни K_HL1 и колеса K_HL2

(3.1)

где N_HO1=10·10⁶ циклов – число циклов перемены напряжений, соответствующее пределу выносливости [4];

N₁ – число циклов перемены напряжений за весь срок службы

(3.2)

где ω₂ - угловая скорость быстроходного вала,

L_h = 7∙365∙24∙0,8 = 49000 ч. – срок службы привода;

Т.к. , то принимаем K_HL1 = 1.

(3.3)

где N_HO2=10·10⁶ циклов – число циклов перемены напряжений, соответствующее пределу выносливости [4];

N₂ – число циклов перемены напряжений за весь срок службы

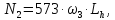(3.4)

где ω₃- угловая скорость тихоходного вала,

L_h = 49000 ч. – срок службы привода;

Т.к., то принимаем K_HL2 = 1.

Определяем допускаемое контактное напряжение, соответствующее пределу выносливости при числе циклов перемены напряжений N_HO1 и N_HO2

(3.5)

(3.6)

Определяем допускаемые контактные напряжения для зубьев шестерни и колеса

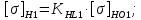(3.7)

(3.8)

Расчет будем вести по наименьшему значению из полученных, то есть .

3.2 Расчет допускаемых напряжений изгиба

Определяем коэффициент долговечности для зубьев шестерни K_FL1 и колеса K_FL2

(3.9)

(3.10)

где циклов – число циклов перемены напряжений, соответствующее пределу выносливости [4];

N₁ – число циклов перемены напряжений за весь срок службы.

Т.к. N₁>N_FO и N₂>N_FO, то принимаем K_FL1=K_FL2 = 1.

Определяем допускаемое напряжение изгиба соответствующее пределу изгибной выносливости при числе циклов перемены напряжений

(3.11)

(3.12)

Определяем допускаемые напряжения изгиба для зубьев шестерни и колеса

(3.13)

(3.14)

Расчет будем вести по наименьшему значению из полученных, то есть

3.3 Проектный расчет закрытой конической зубчатой передачи

Диаметр внешней делительной окружности колеса

(3.15)

где - вспомогательный коэффициент для конической передачи [4];

u – передаточное число редуктора;

T₃ – вращающий момент на тихоходном валу, Н·м;

- допускаемое контактное напряжение колеса,;

- коэффициент, учитывающий распределению нагрузки по ширине венца; .

- коэффициент, учитывающий внутреннюю динамику нагружения; .

Определяем углы делительные конусов колеса и шестерни

(3.16)

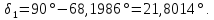
Конусное расстояние

; (3.17)

;

Ширина колес

; (3.18)

Определяем модуль передачи

(3.19)

где

– коэффициент для прирабатывающихся прямозубых колес;

– динамический коэффициент;

– для прямозубых конических колес;

Определяем число зубьев колеса

(3.20)

.

Округляем полученное значение до целого, получаем .

Определяем число зубьев шестерни

(3.21)

.

Округляем полученное значение до целого, получаем .

Определяем фактическое передаточное число u_ф и проверяем его отклонение от заданного

(3.22)

(3.23)

Определяем фактические основные геометрические параметры передачи для шестерни и колеса:

фактические углы делительные конусов колеса и шестерни

(3.24)

- делительный диаметр шестерни и колеса

(3.25)

(3.26)

- коэффициенты смещения для шестерни и колеса

(3.27)

- внешние диаметры зубьев шестерни и колеса

(3.28)

(3.29)