математические модели в экономике (Учебное пособие «Математические модели в экономике», автор М. Г. Сидоренко, 2000 г вариант 11

Факультет дистанционного обучения

Томский государственный университет

систем управления и радиоэлектроники (ТУСУР)

Кафедра (экономика)

Контрольная работа

по курсу «Математические модели в экономике»

(Учебное пособие «Математические модели в экономике»,

автор М. Г. Сидоренко, 2000 г.)

Выполнил:

студент ТМЦДО

гр.:

специальность 080502

г. Шарыпово

2011 г

Вариант №11

Задание 1

Объем выпуска продукции Y зависит от количества вложенного труда x как функция Y(x)=1.5x²-x. Цена продукции v=10, p=290. Другие издержки не учитываются. Найти оптимальное количество вложенного труда.

Решение

Прибыль определяется: W = vY- px = 10(1,5x² – x)- 290x

Воспользуемся соотношением v(df / df) = p, для нахождения оптимального объема производства: 10*1,5/(2x-1)=290.

Следовательно, x=38,8 – оптимальное количество вложенного труда.

Максимальная прибыль при x=38,8:

W=10*(1,5*38,8²-38,8)-290*38,8=10941,6.

Выпуск продукции при x=38,8 равен Y=1,5*38,8²-38,8=2219,36.

Задание 2

Даны зависимость спроса D и предложения S от цены. Найдите равновесную цену, при которой выручка максимальна и эту максимальную выручку. D=100-p; S=20+p.

Решение

Точка равновесия характеризуется равенством спроса и предложения, т.е. 100-p=20+p. Равновесная цена p^*=40 и выручка при равновесной цене W(p*) = p* x D(p*) = p* x S(p*) = 40*(100-40)=2400

При цене p>p^* объем продаж и выручка определяется функцией спроса, при p<p^*- предложения. Необходимо найти цену p’, определяющую максимум выручки:

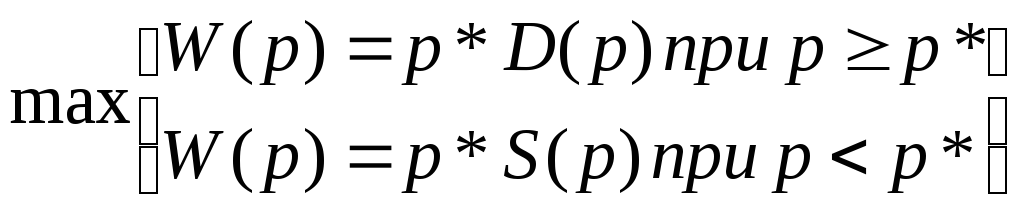
При p*(100-p) максимум достигается в точке p’=50 (определяем максимум через производную), выручка W(50)=50*(100-50)=2500.

При p*(20+p) максимум достигается в точке p’=10, выручка W(10)=10*(20+10)=300.

Таким образом, максимальная выручка W(p)=2500 достигается не при равновесной цене.

Задание 3

Найдите решение матричной игры (оптимальные стратегии и цену игры).

Решение

Решим игру . Сначала необходимо проверить наличие Седловой точки, так как если она есть, то решение игры ясно. Седловой точки нет.

Обозначим оптимальную стратегию Первого Х

1 – Х,

искомую оптимальную стратегию Второго (y, 1-y). Выигрыш Первого есть случайная величина с таким рядом распределения:

Находим средний выигрыш за партию Первого – математической ожидание случайной величины W(x,y):

M(x,y)=3xy-3x(1-y)-2(1-x)y+1(1-x)(1-y)=3xy-3x+3xy-2y+2xy+1-x-y+xy=9xy-4x-3y+1=9x(y-4/9)-3(y-4/9)-1/3=9(y-4/9)(x-3/9)-1/3

Для нахождения оптимальных стратегий игроков необходимо, чтобы М(х,у^*) <= М(х^*,у^*) <= М(х^*,у). Это выполняется при x^*= 1/3 и y^*= 4/9, так как именно в этом случае M(x,4/9)=М(1/3,4/9)=М(1/3,y)=-1/3.

Следовательно, оптимальная стратегия

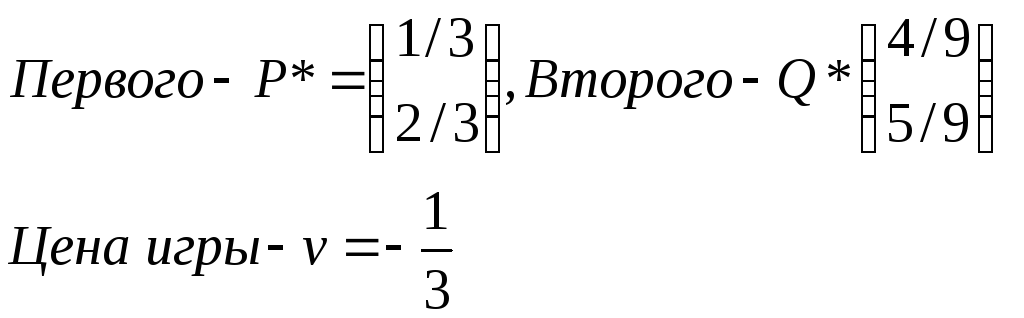
Задание 4

Для трехотраслевой экономической системы заданы матрицы коэффициентов прямых материальных затрат и вектор конечной продукции 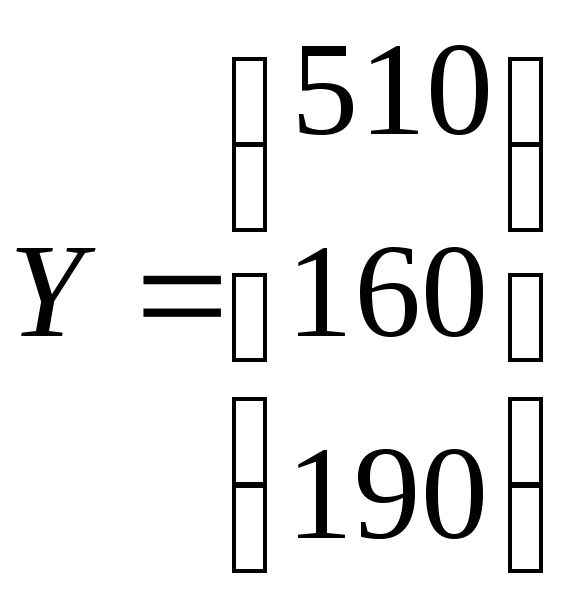. Найти коэффициенты полных материальных затрат двумя способами (с помощью формул обращения невырожденных матриц и приближенно), заполнить схему межотраслевого баланса.

Решение

1. Определим матрицу коэффициентов полных материальных затрат по второму способу, учитывая косвенных затраты до 2-го порядка включительно. Запишем матрицу коэффициентов косвенных затрат 1-го порядка:

Матрицу коэффициентов 2-го порядка:

Таким образом, матрица коэффициентов полных материальных затрат приближенно равна:

Определим матрицу коэффициентов полных материальных затрат с помощью формул обращения невырожденных матриц (первый способ).

А) находи матрицу (Е-А):

Б) вычисляем определитель этой матрицы:

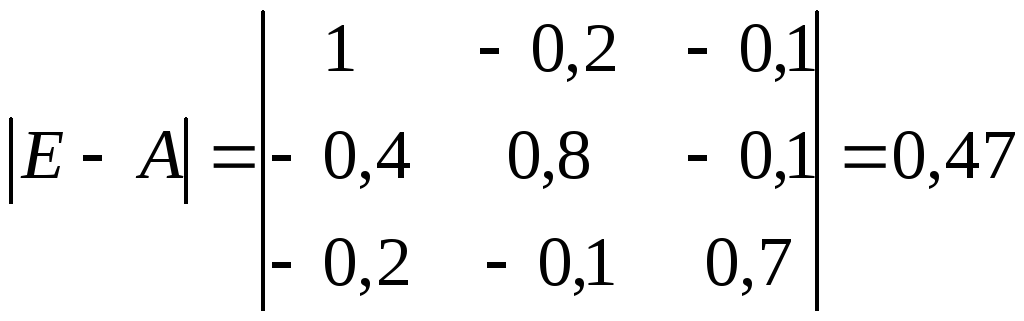
В) транспонируем матрицу (Е-А):

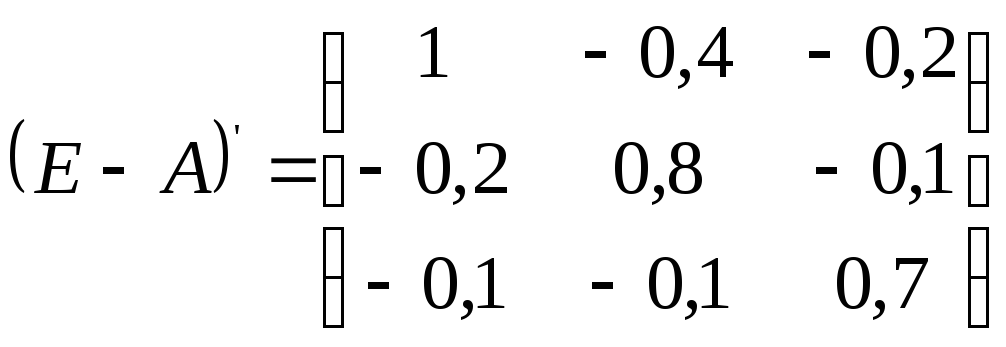
Г) находим алгебраические дополнения для элемента матрицы (Е-А)’:

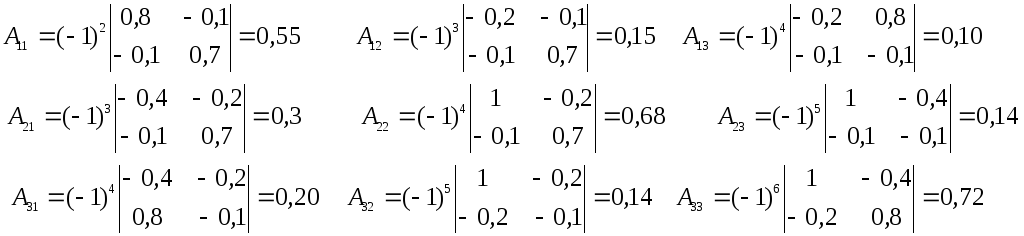
Таким образом, присоединенная к матрице (Е-А) матрица имеет вид:

Д) находим матрицу коэффициентов полных материальных затрат:

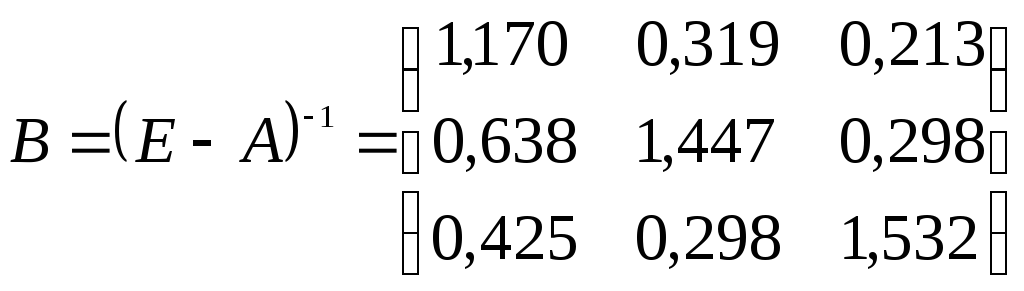
2. Найдем величины валовой продукции трех отраслей (вектор X), используя формулу:

3. Составляем схему межотраслевого баланса, для получения первого квадранта нужно элементы первого столбца заданной матрицы А умножить на величину X₁=688,2; элементы второго столбца матрицы А умножить на X₂=613,5; элементы третьего столбца умножить на X₃=555,5.

Производящие отрасли	Потребляющие отрасли
	1	2	3	Конечная продукция	Валовая продукция
1 2 3	0 275,3 137,6	122,7 122,7 61,3	55,5 55,5 166,6	510 160 190	688,2 613,5 555,5
Условно чистая продукция	275,3	306,8	277,9	860
Валовая продукция	688,2	613,5	555,5		1857,2

Задание 5

Проверить ряд y=75, 76, 78, 78, 79, 80, 79, 80, 78, 79 на наличие выбросов методом Ирвина, сгладить методом простой скользящей средней с интервалом сглаживания 3, методом экспоненциального сглаживания (а=0,1), представить результаты сглаживания графически, определите для ряда трендовую модель в виде полинома первой степени (линейную модель), дайте точечный и интервальный прогноз на три шага вперед.

Решение

А) Проверим ряд на наличие выбросов методом Ирвина. Метод Ирвина Служит для выявления аномальных уровней, т.е. – это отдельное значение временного ряда которое не отвечает потенциальным возможностям исследуемой экономической системы и которое, оставаясь в качестве значения уровня ряда, оказывает существенное влияние на значение основных характеристик временного ряда, и на трендовую модель.

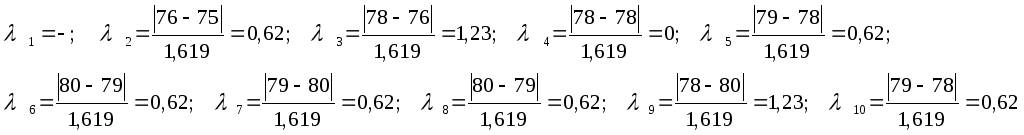
Расчётные значения:

t	1	2	3	4	5	6	7	8	9	10
	-	0,62	1,23	0	0,62	0,62	0,62	0,62	1,23	0,62

Необходимо, расчётные значения сравнить с табличными критерия Ирвина , и если окажется, что расчётное больше табличного, то соответствующее значение уровня ряда считается аномальным.

Табличные значения для уровня значимости a=0,05, т.е. с 5% ошибкой:

n	2	3	10	20	30	50	100
	2,8	2,3	1,5	1,3	1,2	1,1	1

Таким образом, при сравнении значений, обнаруживаем, что аномальных уровней нет, т.е. .

Б) Сгладим методом простой скользящей средней с интервалом сглаживания m=3:

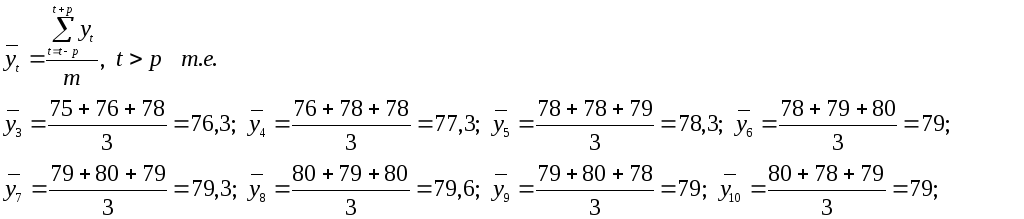
t		Метод простой скользящей средней,
1	75	--
2	76	--
3	78	76,3
4	78	77,3
5	79	78,3
6	80	79
7	79	79,3
8	80	79,6
9	78	79
10	79	79

С) Сгладим экспоненциальным методом с а=0,1 – параметр сглаживания:

t		Экспоненциальный метод,
1	75	76,17
2	76	76,15
3	78	76,34
4	78	76,51
5	79	76,80
6	80	77,12
7	79	77,31
8	80	77,58
9	78	77,62
10	79	77,76

Д) Представим результаты графически:

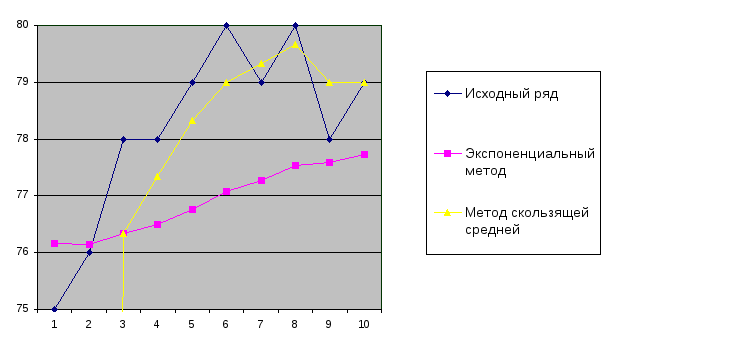
Е) Определим для ряда трендовую модель в виде полинома первой степени (линейную модель):

Необходимо оценить адекватность и точность построения модели, т.е. необходимо выполнение следующих условий:

а) Проверка случайности колебаний уровней остаточной последовательности:

Проверку случайности уровней ряда проведем по критерию пиков, должно выполняться:

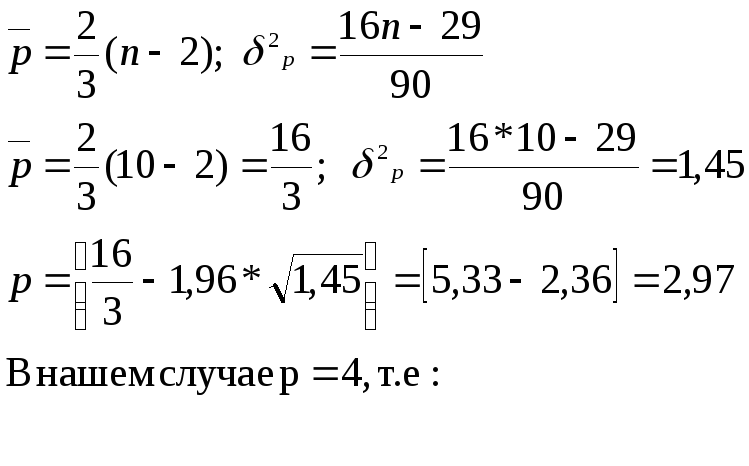
2,97<4 – Условие не выполняется, значит, свойства случайности ряда не выполняется. Модель считается неадекватной.

t	Фактическое	Расчётное	Отклонение	Точки пиков
1 2 3 4 5 6 7 8 9 10	75 76 78 78 79 80 79 80 78 79	76,46 76,85 77,23 77,62 78,01 78,40 78,79 79,17 79,56 79,95	1,46 0,85 -0,77 -0,38 -0,99 -1,6 -0,21 -0,83 1,56 0,95	-- 0 0 1 0 1 1 0 1 --
55	782	782,04	0,04	4

б) Проверка соответствия распределения случайной компоненты нормальному закону распределения:

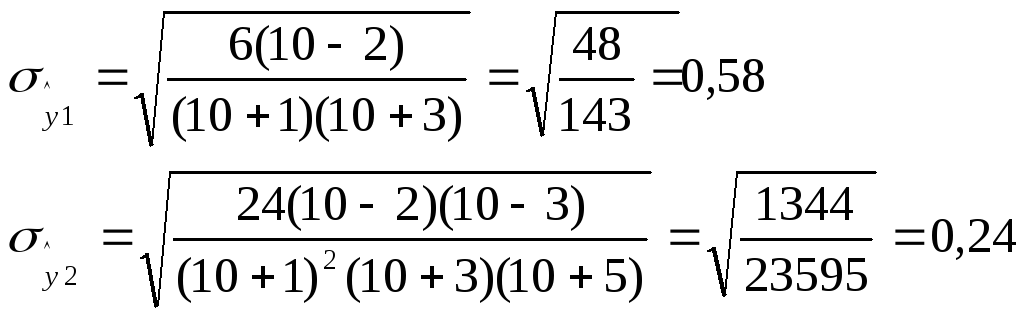
Необходимые условия:

Если эти условия выполняются одновременно, то гипотеза о характере распределения случайной компоненты принимается, если выполняется хотя бы одно из следующих неравенств:

то гипотеза о нормальном распределении отвергается, трендовая модель признаётся неадекватной.

1)

2)

Таким образом, ни одно из неравенств не выполняется, трендовая модель неадекватна, значит, дальнейшее исследование не имеет смысла. Но мы попробуем.

Ж) Точечный и интервальный прогноз на три шага вперед.

Точечный

11 = 76,07 + 0,388 * 11 = 80,34

12 = 76,07+ 0,388 * 12 = 80,73

13 = 76,07 + 0,388 * 13 = 81,11

Вычислим значения величины К путём их линейной экстраполяции приведённых имеющихся значений для числа уровней в ряду n = 11, 12, 13.

По таблице значений величина К для t = 10 (L = 1) K = 1,77

Для t = 11 (L= 1) K = 1,88

Для t = 12 (L= 2) K = 1,73

Для t = 13 (L= 3) K = 1,68

Время t	Шаг L	Точечный прогноз	Доверительный интервал прoгноза
			Нижняя граница	Верхняя граница
11 12 13	1 2 3	80,34 80,73 81,11	71,2 72,3 72,9	89,5 89,1 89,3

Определим среднюю квадратическую ошибку прогнозируемого показателя

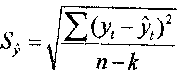((76,07 – 80,34) +(76,07 – 80,73)+(76,07 – 81,11))² / 10 –1,77

= -23,71, извлечём корень = 4,87

Ввиду того, что трендовая модель неадекватна выясним по формуле среднюю относительную ошибку аппроксимации по формуле:

а) для трендовой модели по методу простой скользящей средней:

1/8*(0,022+0,009+0,009+(-0,004)+0,005+0)*100%=0,5%

б) для трендовой модели по экспоненциальному способу:

1/10*(-0,0156+(0,0019)+0,021+0,019+0,028+0,036+0,021+0,0302+0,005 +0,016) *100%=1,59%

Можно выбрать для прогноза трендовую модель по методу простой скользящей средней, как наиболее точную.

Задание 6

Пункт по ремонту квартир работает в режиме отказа и состоит из двух бригад. Интенсивность потока заявок , производительность пункта . Определить вероятность того, что оба канала свободны, один канал занят, оба канала заняты, вероятность отказа, относительную и абсолютную пропускные способности, средне число занятых бригад.

Решение

Рассчитаем коэффициент использования - количество заявок, поступающих за время использования одной заявки.

Далее:

а) Вероятность того, что оба канала свободны:

б) Вероятность того, что один канала занят:

с) Вероятность того, что оба канала заняты:

Отсюда:

д) Вероятность отказа в заявке:

е) Относительная пропускная способность:

ж) Абсолютная пропускная способность:

з) Среднее число занятых бригад: