
3 Контрольные вопросы
1. Объяснить порядок вычисления затрат по номограмме 1.
2. От чего зависит быстродействие рассмотренного в работе алгоритма распределения затрат.
3. В чем суть закона Гроша для вычислительных систем.
Алгоритмизация задачи распределения стоимостных затрат при проектировании вычислительных систем
Цель работы: освоить метод распределения затрат на разработку вычислительных систем с использование мультипликативного критерия оценки качества проектных решений.
Теоретическая часть
Рассматриваемая задача относится к классу задач оптимального использования ресурсов для получения максимума целевой функции. Данная задача имеет актуальный характер при проектировании интегрированных высокопроизводительных вычислительных систем, поскольку качество работы подсистем как правило, напрямую зависит от стоимостных затрат и влияет непосредственно на величину обобщенного критерия.
Предположим, что максимум целевой функции работы ВС maxE(X) определяется максимумом обобщенного критерия мультипликативного вида:
K=D1(z1)D2(z2)D3(z3)D4(z4), (1)
где D1(z1)-D4(z4) – параметры оценки качества подсистем (например – оценки достоверности принятия решения для каждой подсистемы), соответственно: контроля, диагностирования, прогнозирования и принятия решений;
z1-z4 – стоимостные затраты для обеспечения проектных значений параметров подсистем, причем:
z1+z2+z3+z4 ZS,
где ZS – максимально возможные затраты на систему.
Рассмотрим один из методов распределения затрат.
Для распределения стоимостных затрат определяется их минимальное приращение Δz, которое может быть выделено из ZS для изменения параметра Dj (j=1,4).
Выбор Δz определен требуемой точностью при распределении затрат и временем работы компьютера при выборе оптимального варианта. Малая величина Δz приводит к увеличению времени счета компьютера. Большая -приводит к увеличению погрешности в распределении затрат.
Если предположить, что Δz составляет некоторое число процентов от ZS, то число возможных приращений ресурса W= ZS / Δz . Число возможных комбинаций V в распределении процентов ZS по подсистемам определяется числом комбинаций (k1k2k3k4)i , где k1-k4 представляют собой число приращений ресурса ZS, распределенное по подсистемам (i=1÷V, где V – максимально возможное число вариантов), причем k1+k2+k3+k4=N. Тогда zj=Δzkj (i=1÷4). Например, если ZS=100000 рублей, Δz=5 тыс.рублей, W=20, k1=5, k2=2, k3=1, а k4=12, то затраты будут распределены по подсистемам, как z1=5000*5, z2=5000*2, z3=5000*1 z4=5000*12 рублей.
Выбор оптимального варианта распределения затрат производится путем перебора комбинаций k1k2k3k4. По априорно известным зависимостям Dj=fj(z) для каждой комбинации (k1k2k3k4)i определяются сомножители Dj (j=1÷4) и величины Ki (i=1÷V) по формуле (4.1). При этом формируются векторы параметров:
Mi={(k1,k2,k3,k4)i , (z1,z2,z3,z4)i , (D1,D2,D3,D4)i , Ki , (Z)i} i=1,2,3, ... , V.
Величина критерия для оптимального варианта распределения ресурса определяется как максимальная величина произведения (6.1), полученная на множестве всех вариантов, в соответствии с выражением:
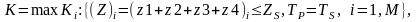
где TP и TS – соответственно реальное и допустимое время выбора оптимального варианта.
Рассмотренный алгоритм описан программой и позволяет определить оптимальный вариант распределения ресурса для любых функций D=f(z). Например, для модельных функций вида:
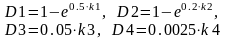
- при Δz =5, S=100, W=20 получены следующие результаты: общее число вариантов V=4845, оптимальная комбинация вкладов k1k2k3k4 стоимостного ресурса: 02030510, т.е. k1=2, k2=3, k3=5, k4=10; максимальная величина критерия Kmax=0,01783, время счета компьютера – не более 1 сек. Программа и алгоритм могут быть использованы при любых реальных видах функций D(z) и исходных данных задачи.
Постановка задачи
- Построить схему алгоритма программы распределения затрат по критерию максимального мультипликативного критерия;
- по данным варианта из таблицы 4.1 определить число комбинаций распределения затрат в соответствии с алгоритмом решения задачи и оценить время решения задачи, если известно время вычисления одной комбинации Δt;
- сделать выводы по работе.
Таблица 6 – Варианты заданий
-
Задание
Zs*1000
ΔZ
N
Δt*0.001
Вариант
тыс.р.
тыс.р.
сек.
1
10
5
4
0.1
2
20
10
5
0.01
3
30
25
10
0.001
4
40
5
100
0.1
5
50
10
10
0.01
6
60
25
20
0.001
7
70
5
50
0.1
8
80
10
100
0.01
9
90
25
10
0.001
10
100
5
20
0.1
11
10
10
50
0.01
12
20
25
100
0.001
13
30
5
10
0.1
14
40
10
20
0.01
15
50
25
50
0.001
16
60
5
100
0.1
17
70
10
10
0.01
18
80
25
20
0.001
19
90
5
50
0.1
20
100
10
100
0.01
Продолжение таблицы 6
-
Задание
Zs*1000
ΔZ
N
Δt*0.001
Вариант
тыс.р.
тыс.р.
сек.
21
10
25
10
0.001
22
20
5
20
0.1
23
30
10
50
0.01
24
40
25
100
0.001
25
50
5
50
0.1
