5. Дайте определение передаточной функции.

Передаточная функция - отношение выходного сигнала к входному в изображениях по Лапласу при нулевых начальных условиях. Недостатки: передаточная функция существует только для линейных стационарных систем. В нестационарных системах один или несколько параметров зависят от времени, поэтому преобразованием Лапласа пользоваться нельзя. В отличие от уравнений состояния передаточная функция не содержит информации внутреннем устройстве системы и не отображает физической природы протекающих в ней процессов. Достоинства: заключаются в том, что она позволяет изобразить причинно-следственную связь между переменными в наглядной схематической форме. Суть операторного метода состоит в том, что для линейных дифференциальных уравнений существует изоморфизм (взаимно-однозначное соответствие) между функциями-оригиналами, входящими в уравнение и их изображениями (образами при преобразовании Лапласа). Применяя преобразование Лапласа к исходному уравнению, переходим от дифференциального уравнения к алгебраическому уравнению для изображений. Затем по функции-изображению, удовлетворяющей этому алгебраическому уравнению, ищется функция - оригинал, являющаяся решением исходного дифференциального уравнения.

Структурная схема - графо-аналитическая форма представления динамической системы.

Правила преобразования структурных схем

Рис. 13 – Последовательное соединение блоков.

При последовательном соединении передаточные функции отдельных блоков перемножаются.

Рис. 14 – Параллельное соединение блоков.

При параллельном соединении передаточные функции отдельных блоков складываются.

Перенос узла через блок против движения сигнала.

Перенос узла через блок по ходу движения сигнала.

положительная обратная связь

Система с обратной связью состоит из прямой цепи и цепи обратной связи .

7. Что такое типовое звено?

Типовым звеном называется часть системы управления, либо вся система, описываемая дифференциальным (или иным) уравнением определенного вида. Наиболее распространенными элементарными звеньями являются: пропорциональное звено; идеальное интегрирующее звено; реальное интегрирующее (апериодическое) звено; инерционно-интегрирующее звено; идеальное дифференцирующее звено;

реальное дифференцирующее звено; изодромное звено; колебательное звено; звено запаздывания.

Идеальное интегрирующее.

В ыходная величина идеального интегрирующего звена пропорциональна интегралу входной величины: Передаточная функция Частотная передаточная функция

, откуда .

ЛАЧХ: ЛФЧХ:

Р еальное интегрирующее.

Передаточная функция Переходная характеристика в отличие от идеального звена является кривой.

 

Идеальное дифференцирующее.

Выходная величина пропорциональна производной по времени от входной:

Частотная функция дифференцирующего звена , откуда

ЛАЧХ и ФАЧХ Модуль частотной характеристики растёт с ростом частоты и стремится к бесконечности. Фазовый угол от частоты не зависит и постоянно равен 90°. АФЧХ располагается вдоль п оложительной полуоси мнимых чисел на комплексной плоскости. Начало АФЧХ, соответствующее частоте , совпадает с началом координат, а при  АФЧХ устремляется в бесконечность.

Р еальное дифференцирующее.

  Идеальные дифференцирующие звенья физически не реализуемы. Большинство объектов, представляющих собой дифференцирующие звенья - реальные дифференцирующим звеньям, передаточные функции которых имеют вид

ЛАЧХ и ФАЧХ:

К олебательным звеном называется один из простейших динамических элементов или его составная часть, имеющая передаточную функцию вида:

ЛАЧХ звена может быть получена следующим образом Первое слагаемое представляет собой постоянную величину L₁(ω)= 20∙lgК - прямую, параллельную оси абсцисс. Второе слагаемое зависит от частоты ω. Если , составляющими T²ω² и 4ξ²T²ω² можно пренебречь по сравнению с 1, поэтому L₂(ω)=0.Если  ,то 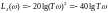. Очевидно, что при изменении частоты ω на декаду, значение L₂(ω) изменится на -40 дБ. Таким образом, приближённая асимптотическая ЛАЧХ колебательного звена изображается двумя отрезками прямых: горизонтальным отрезком, при  , и отрезком с наклоном -40 дБ/дек. Низкочастотные и высокочастотные асимптоты ЛАЧХ сопрягаются при частоте сопряжения ω₁, определяемой из следующего уравнения  , т.е. при частоте  . Точные ЛАЧХ колебательного звена отличаются от асимптотической ЛАЧХ. Эти отклонения в значительной степени зависят от коэффициента относительного затухания ξ, входящего в выражение передаточной функции. Добавляя поправки, соответствующие различным значениям ξ к асимптотической ЛАЧХ, можно получить точные ЛАЧХ. Если построить семейство кривых (ЛАЧХ) для одного и того же значения  и различных значений ξ, то можно показать, что при значениях 0,35 < ξ< 0,75 расхождение между асимптотической и истинными ЛАЧХ не превышает 3 дБ, как и в случае апериодического звена. Поэтому в этом случае можно пользоваться асимптотическими ЛАЧХ. При других значениях ξ асимптотическую ЛАЧХ корректируют с помощью готовых графиков поправок, дающих разность между истинной и асимптотической ЛАЧХ. L(ω) в этом случае строится по расчётным точкам. Если ξ = T₁/2Т₂ ≥1, то колебательное звено превращается в апериодическое звено второго порядка. ЛФЧХ колебательного звена φ(ω) рассчитывается по формулам:  

Н а рисунке представлены эти характеристики при различных значениях коэффициента ξ, из которых видно, что ЛФЧХ колебательного звена изменяется от 0° в области низких частот, до 180^° в области высоких частот. На частоте сопряжения   сдвиг по фазе равен -90°