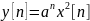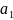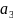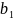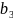5.4. Контрольное задание
5.4.1. Расчет частотных характеристик цепи
На рис. 5.15 показана схема активной линейной цепи. В качестве активных элементов использованы идеальные операционные усилители, имеющие на всех частотах постоянный коэффициент усиления К0=2.
Вид фильтра А иВ определяется номером варианта (табл. 5.1. и 5.2.) а параметры – номером подварианта (5.3).
Требуется:
А) определить выражение для комплексной передаточной функции К(jω);
Б) построить графики АЧХ ( К(f) ) и ФЧХ ( φ(f) );
В) определить полосу пропускания цепи Δ f0.7 (по уровню 0.707 от максимального значения)
5.4.2. Расчет временных характеристик
По полученному выражению К(jω) найдите импульсную h(t) и переходную g(t) характеристики линейной цепи. По уровню 0.1 от максимального значения аналитически или графически определите длительность переходных процессов Δtn.
5.4.3. Устойчивость цепи с обратной связью.
Определите устойчивость исследуемой активной линейной цепи (рис. 5.15) в случае соединения входной и выходной клемм.
14.4. Контрольное задание
14.4.1. ЦИФРОВЫЕ ЦЕПИ И ИХ ХАРАКТЕРИСТИКИ
1. По заданным разностным уравнениям цифровых цепей проверьте их физическую реализуемость (каузальность), стационарность, линейность и устойчивость:
Таблица 14.2
Номер варианта |
Разностное уравнение |
0 |
у[n] = х[n-k]exp(-nk) |
1 |
у[n] = ах[n-k] |
2 |
|
3 |
у[n] = (n+a)х[n-k] |
4 |
|
5 |
у[n] = bх[n+k] |
6 |
у[n] = x[n]sin(an) |
7 |
y[n] = ах[n+k]-x[n] |
8 |
у[n] = bx[n]-cx[n-k] |
9 |
у[n] = х[n+k]exp(-nk) |
Таблица 14.3
Номер подварианта |
а |
b |
с |
к |
1 |
1 |
4 |
3 |
2 |
2 |
3 |
2 |
4 |
1 |
3 |
2 |
3 |
1 |
4 |
4 |
4 |
1 |
2 |
3 |
5 |
2 |
1 |
3 |
4 |
6 |
3 |
2 |
4 |
3 |
7 |
2 |
1 |
4 |
2 |
8 |
3 |
1 |
2 |
4 |
9 |
5 |
2 |
1 |
6 |
0 |
3 |
4 |
6 |
5 |
2. Составьте структурную схему и постройте график импульсной характеристики (первые 10 значений) цифровой цепи, описанной разностным уравнением:
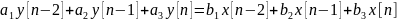
Таблица 14.4
Номер варианта |
|
|
|
Номер подварианта |
|
|
|
1 |
3 |
0 |
I |
1 |
0 |
2 |
5 |
2 |
0 |
4 |
4 |
2 |
2 |
0 |
3 |
3 |
6 |
0 |
3 |
2 |
3 |
2 |
0 |
4 |
2 |
3 |
1 |
4 |
0 |
5 |
2 |
5 |
5 |
0 |
3 |
5 |
2 |
0 |
4 |
6 |
0 |
4 |
2 |
6 |
0 |
0,5 |
2,5 |
7 |
3 |
0 |
2 |
7 |
6.5 |
0 |
3 |
8 |
0 |
2 |
1 |
8 |
0 |
2 |
3 |
9 |
5 |
0 |
2 |
9 |
0 |
2 |
3 |
0 |
0 |
3 |
4 |
0 |
3 |
0 |
8 |
3. По заданному сигнальному графу цифровой цепи найдите разностное уравнение и передаточную функцию цепи:
для четных вариантов для нечетных вариантов
Таблица 14.5
Номер |
|
|
|
|
с |
подварианта |
|
|
|
|
|
1 |
0,5 |
-0,3 |
1,4 |
2,5 |
3,0 |
2 |
1,2 |
2,5 |
-0,5 |
-0,4 |
1,0 |
3 |
2,0 |
-3,2 |
4,0 |
1,2 |
2,2 |
4 |
3,5 |
-5,2 |
-2,5 |
-0,4 |
2,0 |
5 |
-1,2 |
3,5 |
1,4 |
2,5 |
2,4 |
6 |
2.4 |
-1,2 |
3,0 |
3,6 |
-1,2 |
7 |
-2,5 |
-2,4 |
1.0 |
3,2 |
4,4 |
8 |
-0.4 |
2,5 |
3,2 |
2,8 |
2,5 |
9 |
3,5 |
-0,4 |
2,0 |
1,2 |
3,5 |
0 |
-2,5 |
3,5 |
8,25 |
2,8 |
2,6 |