7. Эффект масштаба

Пусть – объем выпускаемой продукции при плане ( ). При увеличении затрат ресурсов (заметим, что здесь речь идет о долговременном планировании, когда возможны изменения всех ресурсов) в k раз (k > 1) выпуск составит . Тогда, если

, т.е. выпуск продукции увеличился тоже в k раз, то наблюдается постоянный эффект от расширения масштабов производства;

, т.е. выпуск продукции увеличился более, чем в k раз, то наблюдается возрастающий эффект от расширения масштабов производства;

, т.е. выпуск продукции увеличился менее, чем в k раз, то наблюдается убывающий эффект от расширения масштабов производства.

Функция нескольких переменных называется однородной порядка m, если для всех х из некоторой области Х.

Для однородной функции задача об эффекте масштаба легко решается.

Если ПФ является однородной порядка m, то

при m=1 ПФ обладает постоянным эффектом масштаба;

при m>1 ПФ обладает возрастающим эффектом масштаба;

при m<1 ПФ обладает убывающим эффектом масштаба.

Пример. Для ПФ Кобба-Дугласа выполняется следующее соотношение

(3)

ПФ типа Кобба-Дугласа является однородной функцией порядка a ₁+ a ₂. ◄

Для однородной функции влияние эффекта масштаба можно наглядно представить графически (см. рис. 5).

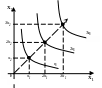
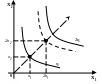
Рис 5. Эффект масштаба (соответственно: постоянный, убывающий, возрастающий).

8. Проблема замещения ресурсов

Предположим, что производитель хочет изменить затраты первого ресурса на величину , не изменяя при этом объем выпускаемой продукции. Выясним, на какую величину необходимо изменить затраты второго ресурса?

В силу неизменности выпуска продукции приращение ПФ при переходе от плана (x₁, x₂) к плану с одной стороны равно 0, а с другой – может быть приближенно заменено ее дифференциалом для всех достаточно малых изменений плана выпуска:

.

Эту формулу можно записать иначе:

.

Предельной нормой технологического замещения второго ресурса первым называется величина (MRTS – marginal rate of technical substitution).

Экономический смысл предельной нормы замещения: , т.е. - это примерное количество второго ресурса, которое можно сэкономить, увеличив затраты первого ресурса на 1единицу, при этом объем выпуска не изменится.

Предельная норма технологического замещения первого ресурса вторым определяется как MRTS₂₁(x₁, x₂)= (MRTS₁₂(x₁, x₂))^-1, если .

Геометрический смысл предельной нормы замещения второго ресурса первым: численно равна тангенсу угла наклона касательной к изокванте в точке (x₁,x₂), взятому с обратным знаком.

В дальнейшем, для удобства, мы будем рассматривать тангенс смежного острого угла, поскольку тангенсы этих углов отличаются только знаком.

Линейная ПФ предполагает полную замещаемость ресурсов, так что данный объем выпуска может быть получен либо при затратах только первого ресурса, либо при затратах только второго ресурса, либо с использованием различных комбинаций того и другого ресурса. Предельная норма замещения ресурсов постоянна для всех планов производства. .

В случае ПФ типа Кобба-Дугласа (рис. 6) непрерывно убывает , т.е. возможна замещаемость ресурсов в определенных границах.

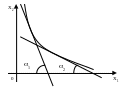
Рис. 6. Изокванта ПФ типа Кобба-Дугласа

Основные свойства предельной нормы замещения ресурсов :

1. численно равна тангенсу острого угла наклона касательной к изокванте в точке (x₁,x₂).

2. .

3. .

4.