Глава 2. Функции в экономическом моделировании.
1. Функция спроса.
Основной задачей экономического анализа является изучение связей экономических величин. Как изменится выручка фирмы при повышении цены на её продукцию? В какой пропорции дополнительное оборудование может заменить выбывающих работников? Для решения подобных задач надо построить функции связи входящих в них переменных, которые затем изучаются с помощью методов дифференциального исчисления. Предельный анализ в экономике – совокупность приемов исследования изменяющихся величин на основе анализа их предельных значений. Предельный показатель функции – это её производная (в случае функции одной переменной) или частные производные (в случае функций нескольких переменных).
Рассмотрим для примера важнейшую экономическую зависимость – функцию спроса. Исследуемая величина спроса на определенный товар за некоторый период времени является эндогенной переменной, обозначим её буквой x. Она зависит от многих факторов (экзогенных переменных): цены этого товара p, дохода потребителей, цен других товаров (дополняющих или замещающих) и других факторов, которые не всегда можно количественно измерить, например, моды, рекламы, инфляционных ожиданий. Если зафиксировать все факторы, кроме цены, то мы получим самую простую модель – функцию одной переменной, задающую зависимость спроса от цены x=x(p). Как и другие функции, функцию спроса можно задать дискретно таблицей соответствующих значений (эмпирические данные), можно на основе статистических данных методами эконометрики вывести формулу зависимости (математическая модель), а можно нарисовать кривую спроса (графическая модель).
Чтобы измерить, насколько изменяется исследуемый показатель при изменении фактора, имеются два подхода: приростный и темповый.
Если рассматривать
абсолютный прирост переменной
(изменение аргумента
x)
и вызываемый им прирост
(изменение значения функции
),
то в качестве меры «абсолютной»
чувствительности может служить: средняя
скорость изменения функции
или предельная скорость
– производная. При этом подходе прирост
функции оценивается с помощью производной
.
Отсюда экономический
смысл предельной величины
(производной): она примерно равна приросту
функции при изменении аргумента на одну
единицу (предполагается, что эта единица
– достаточно малая величина).
Как правило, величина спроса на какой-либо товар уменьшается при увеличении его цены (исключая товары Гиффина, для которых не выполняется закон спроса). Это отражается в отрицательном наклоне кривой спроса и в том факте, что функция спроса обычно убывает.
П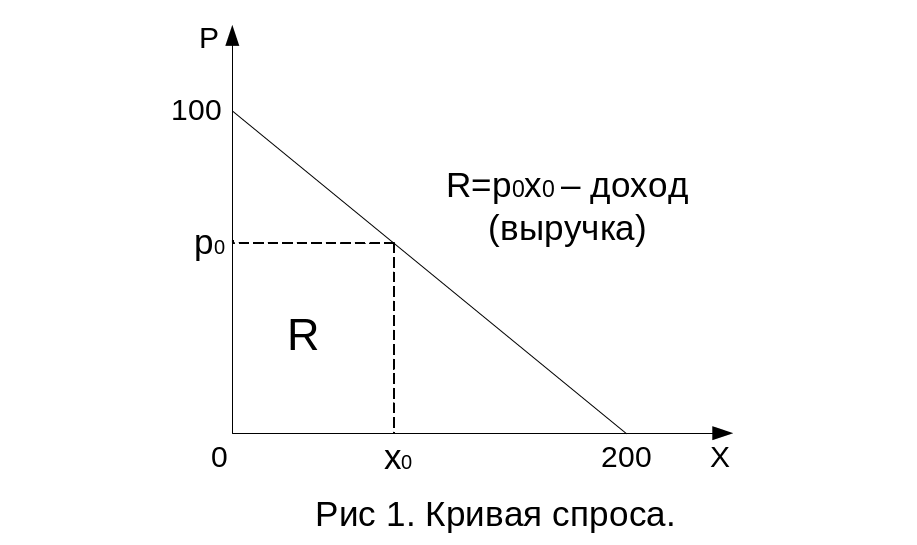
ример.
Функция спроса на сахар в одном населенном
пункте в кг за день задана в виде
(где
p
- цена в руб. за кг). Это так называемая
прямая функция
спроса, которая позволяет устанавливать
величину спроса при подстановке значений
цены. Например: при цене на сахар 20 руб.
его потребление составит 160кг.
А для построения графика
функции спроса – кривой спроса (по
традиции в системе координат xOp)
– удобно выразить
p
через x
и получить обратную
функцию спроса p=100-0.5x.
Учитывая неотрицательность всех
переменных, имеем ограничения:
.
Кривая спроса расположена в первой
четверти. В данном примере функция
спроса линейна, её графиком является
прямая линия с отрицательным углом
наклона.
.
Производная везде одинакова. Её величина
означает, что если увеличить цену на
1рубль (прирост цены
),
то спрос уменьшится на 2кг (
).
◄
Производная отражает абсолютную величину падения спроса при повышении цены. Но величина станет другой, если измерять сахар в других единицах (не в кг, а в тоннах). В этом кроется недостаток производной функции спроса как меры чувствительности спроса - она зависит от единиц измерения величин. В отличие от абсолютного прироста (при увеличении цены сахара с20 до 25 рублей он составит 25-20=5 рублей), относительный прирост 5/20=1/4=25% не связан с единицами измерения.