
matematika экзамен
.docx
|
1.Матрицы.Действия с матрицами. Матрицы позволяют записать в простой форме значительную часть математ-ого ур-ния dimA=mxn
– размерность матрици(число строк*число
столбцов) Сложение матриц: возможно только,тогда когда совпадает их размерность A= Умножение
матриц на число: Умножение
матриц: чтобы умножение АВ было
возможным, надо чтобы число столбцов
левой матрицы=числу строк правой
матрицы, dimA=mxn,
то dimB=nxp,
где m
и p
– любые числа , АВ=ВА, но АВ А=
Вычитание
матриц: А=
|
2.Ступенчатая матрица. В=
Ступенчатой называется матрица , удовлетворяющая следующим условиям: 1)если эта матрица содержит нулевую строку, то все строки расположенные под нею так же нулевые 2)если первый нулевой элемент некоторой строки расположен в столбце с номером n,то первый нулевой элемент след.строки должен находится в столбце с номером больше чем n. 3.Определитель матрицы. Матрицу
А можно поставить в соответствующее
число
1)если
А=(а), тогда определитель этой матрицы
2)если
А= 3)А=
|
|
4.Миноры и их алгебраические дополнения. 1)Минор- определитель оставшейся части, определитель размерности, который получается вычеркиванием элементов. А= 2)
Алгебраическое дополнение
Теорема
Лапласа:
Аналогичное
разложение
Некоторые св-ва определителя: 1)если матрица содержит нулевую строку или столбец , то ее определитель =0 2)при смене местами двух строк или столбцов определитель меняет знак 3)определитель не меняется, если в строку прибавить любую строку, умноженную на число. 4)если определитель имеет 2 порпорциональные строки или столбца, то он =0
|
5.Вычисление определителей второго и третьего порядков. 1)чтобы
вычислить определитель матрицы
второго порядка, надо от произведения
элементов главной диагонали отнять
произведение элементов побочной
диагонали.
2)для вычисления определителей третьего порядка существует: Правило
треугольника:произведение элементов
в первом определители берется со
знаком +, для второго –со знаком -.
Правило
Саррюса: справа от определителя
дописывают первых два столбца и
произведения элементов на главной
диагонали и на диагоналях,ей параллельных,
берут со знаком +, а произведения
элементов побочной диагонали –со
знаком -.
|
|
6.Вычисление определителей разложением по элементам строки или столбца. 1)по элементам строки: определитель матрицы А равен сумме произведений элементов строки на их алгеброическое дополнение
|
2)по элементам столбца: определитель матрицы А равен сумме произведений элементов столбца на их алгебраическое дополнение |
|
7.Ранг матрицы. Способы определения ранга.
Метод перебора миноров: 1)если есть хотя бы один элемент матрицы, отличный от 0, то ранг матрицы =1(т.к. есть минор первого порядка не равный 0) 2)если все миноры второго порядка равны 0, то ранг матрицы=1 3)если все миноры третьего порядка равны нулю, то ранг матрицы = 2. Элементарные преобразования матрицы(методом Гауса): 1)перестановка местами строк(или столбцов) матрицы; 2)умножение всех элементов какой-либо строки(столбца)матрицы на произвольное число k, отличное от 0. 3)прибавление к элементам какой-либо строки(столбца) соответствующих элементам другой строки (столбца) матрицы, умноженных на произвольное число k.
|
9.Решение систем линейных ур-ний методом Гауса.
1)если
2)если
3)если
10.Решение систем ур-ний методом Крамера. – это Способ решения квадратных систем линейных ур-ний с нулевым определителем основной матрицы. |
|
11.Векторы.Действия с векторами.
1)Сложение векторов
2)Умножение векторов на число λ
3)Вычитание векторов
4)Эквивалентное построение
|
12.Определение углов между векторами с помощью их скалярного произведения.
Замечание:
3)Сочетания из n по K Это любой неупорядоченный набор из К различных элементов, выбранных из генеральной совокупности в n элементов. |
|
15.Элементы комбинаторики: перестановки,размещения,сочетания. Если
в результате опыта могут произойти n
равновозможных событий, среди которых
m
случаев благоприятных событий А, то
Р(А)= 1)Перестановки: перестановкой из n элементов называется любой упорядоченный набор этих элементов.
Число
различных перестановок из n
элементов обозначается
2)Размещение из n по K Это любой упорядоченный набор из К различных элементов, выбранных из генеральной совокупности в n элементов.
|
16. События невозможные, достоверные, случайные. События совместные и несовместные. 1)Достоверные- это событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий S. Пр.:если в сосуде содержится вода при нормальном атмосф. Давлен. И t=20, то событие «вода в сосуде находится в жидком состоянии» - есть достоверное. Заданные атмосф.давл. и температура воды составляет совокупность условий S. 2)Невозможные –событие, которое заведомо не произойдет, если будет осуществлена совокупность условий S.Пр.:событие «вода в сосуде находится в твердом состоянии» заведомо не произойдет,если будет осуществлена совокупность условий предыдущего примера. 3)Случайные –событие, которое при осуществлении совокупности условий S может либо произойти, либо не произойти. Пр.:если брошена монета, то она может упасть так, что будет либо орел, либо решка. Поэтому событие при событие «при бросании монеты выпал орел»- слуайное. 4)Совместные события- события А и В, если в результате испытания они могут наступить вместе. Совместные события содержат в себе общие элементарные исходы.Пр.:выпадение четного числа очков кратного трем, при подбрасывании кубика 5)Несовместные события- события Аи В, если в результате испытания они никогда не могут наступить вместе. Они не содержат в себе общих элементарных исходов. Пр.:выпадение 3и6 при подбрасывании кубика. |
|
17.Классическое определение вероятности события. Геометрические вероятности. 1)Классическое
определение вероятности предполагает,
что число элементарных исходов
испытания конечно. Если в результате
опыта могут произойти n
равновозможных событий, среди которых
m
случаев благоприятных событий А, то
Р(А)= 2)Геометрическая вероятность-вероятность попадания точки в область .
Некоторые операции над множителями.
20.Формула полной вероятности. Пусть события
|
18.События зависимые и независимые.Условная вероятность события. 1)Несколько событий называются независимыми, если любое из них не зависит от любого другого события и от любой комбинации остальных. 2)События называются зависимыми, если одно из них влияет на вероятность появления другого. 3)Условная вероятность – вероятность одного события В, вычисленная при условии, что событие А произошло.
19.Теоремы умножения и сложения. 1)Теорема о сложении:вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий.
Вероятность суммы совместных событий вичисляется:
2)Теорема умножения:вероятность произведения независимых событий АиВ :
Вероятность произведения зависимых событий А и В:
|
|
21.Повторные независимые события.Формула Бернули. Производится серия из n одинаковых опытов, в каждом из которых может появиться событие А с вероятностью Р. Какова вероятность,что это событие появляется К раз?
Вероятность такого случая= Число различных расположений
Пр.:Какова вероятность, что при 5 бросаний игральн.костей шестерка выпадет 2 раза? n=5, K=2, p= , q= .
|
22.Наивероятнейшее число появлений события -//-//-
(А) в n
независимых событий называется такое
число для которого вероятность,
соответствующая этому числу, превышает
или не меньше вероятности каждого из
остальных возможных чисел появления
события (А).
23.Асимптотическая (локальная) формула Лапласа. Если число n опытов велико,то прибегают к фор-ле Лапласа: |
|
24.Интегральная формула Лапласа.
Когда
n
|
25.Дискретная случайна я величина. Закон распределения вероятностей случайной величины. В общем случайная величина полностью характеризуется таблицей вида:
Которая называется рядом распределения с.в.,если
Законом распределения с.в. называют соответствие между возможными значениями и их вероятностями. |
|
26.Равномерное и биноминальное распределение дискретной случайной величины. 1)Биноминальное распределение: если ряд распределений описывается бернулевской вероятностью, т.е. имеет вид
То говорят что ряд имеет биноминальное распределение. Бином Ньютона:
2)
Равномерное распределение с.в. полностью
определяется двумя параметрами: а
и в-интервалом,
на котором определена с.в .Можно
определить параметры а
и в
равномерного
распределения по известным значениям
математического ожидания
|
27.Математическое ожидание дискретной случайной величины. Исходя из ряда распределения случайных величин, определяется числом:
Свойства М(х): 1.М(С)=С, где С- не случайная величина. Док-во: 2.М(С*Х)=С*М(Х) Док-во:
3.М(Х*У)=М(Х)*М(У) Док-во:
4.М(Х+У)=М(Х)+М(У) Док-во:
|
|
28.Дисперсия дискретной случайной величины.Среднее квадратическое отклонение. 1)
Дисперсия дискретной случайной
величины
Свойства
1.D(C)=0 2.D(CX)= 3.D(X+Y)=D(X)+D(Y)
|
|

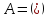
 В=
В=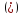 А+В=
А+В=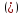
 ;
;

 ВА
ВА В=
В=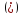
 В=
В=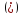 А-В=
А-В=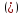
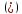 - расширенная матрица. Процесс
приведения матрицы к ступенчатому
виду совпадает с приведением по Гаусу.
- расширенная матрица. Процесс
приведения матрицы к ступенчатому
виду совпадает с приведением по Гаусу.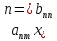
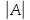 :
: =а
=а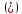 ,
то
,
то
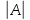 =
=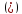 ;
;
 =
= =
=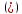 ;
;
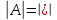

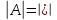 ;
;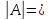
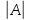 можно
производить по элементам любой строки
или столбца.
можно
производить по элементам любой строки
или столбца. =
= =
=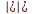 =
=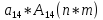 -
называется
наивысший порядок минора, содержащегося
в матрице отличного от 0. Для того,
чтобы определить ранг матрицы,надо
все привести к ступенчатому виду
-
называется
наивысший порядок минора, содержащегося
в матрице отличного от 0. Для того,
чтобы определить ранг матрицы,надо
все привести к ступенчатому виду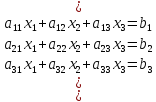 - эту систему
приводят к виду эквивалентными
преобразователями.
- эту систему
приводят к виду эквивалентными
преобразователями.
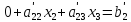 0+0+
0+0+
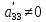 ,
то система имеет единственное решение
,
то система имеет единственное решение
 ,
то система решений не имеет
,
то система решений не имеет ,
то система имеет множество решений
,
то система имеет множество решений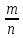

 .
Пр.:в урне 6бел. И 4 черн.шара.Извлекли
1 шар.Какова вероятн.соб.,что шар белый?
N=10,m=6,
Р(А)=
.
Пр.:в урне 6бел. И 4 черн.шара.Извлекли
1 шар.Какова вероятн.соб.,что шар белый?
N=10,m=6,
Р(А)= .
.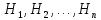 образуют такую группу событий:
образуют такую группу событий:
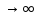 ,
то используется интегральная фор-ла
Лапласа для случая
,
то используется интегральная фор-ла
Лапласа для случая
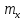 и дисперсии
и дисперсии
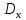 c.в.
c.в.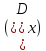 -называют
математическое ожидание квадрата
отклонения с.в. от ее математического
ожидания.
-называют
математическое ожидание квадрата
отклонения с.в. от ее математического
ожидания. :
: D(X)
D(X)