Лабораторная работа №4. Решение симплекс-методом задачи линейного программирования

Цель работы:

Целью лабораторной работы является получение навыков самостоятельной алгоритмической и программной реализации на компьютерной технике симплекс-метода решения задачи линейного программирования в MatLab, научиться сводить оптимизационные задачи к задаче линейного программирования, заданную в допустимом каноническом виде, научиться представлять результаты расчетов в виде html-страниц.

Требования к содержанию, оформлению и порядку выполнения

Номер варианта индивидуального задания определяется последней цифрой в зачетной книжке студента (цифра 0 соответствует варианту № 10) или порядковым номером компьютера в компьютерном классе, за которым работает студент.

Лабораторные работы заключаются в изучении и программной реализации методов, рассмотренных в теоретическом курсе дисциплины.

Перед работой непосредственно на компьютере студенты обязаны внимательно изучить соответствующий теоретический материал, разобрать примеры, представленные на лекциях.

Программирование методов, указанных в заданиях лабораторных работ, следует выполнять самостоятельно, используя команды языка программирования пакета Matlab.

После завершения создания m-файлов в пакете Matlab, реализующих указанные методы, следует выполнить вычисления на основании данных своего варианта. Обязательно следует выполнить проверку полученных на компьютере результатов вычислений.

Отчет оформляется в соответствии с приведенным образцом.

Отчет о выполнении задания лабораторной работы должен содержать следующие разделы:

1. Формулировка задания на программирование.

2. Краткое описание исследуемого метода - фрагмент лекционного материала.

3. Текст программы в виде m-файла - является основным результатом выполнения работы.

4. Исходные данные, номер варианта.

5. Результаты вычислений, включая промежуточные результаты - копии текстовых файлов или копии экранных форм, графики.

6. Результаты проверки полученных данных

Общая постановка задачи

В результате выполнения заданий лабораторной работы студенты должны уметь создавать программно-алгоритмическую поддержку для компьютерной реализации симплекс-метода решения задачи линейного программирования в MatLab, научиться сводить оптимизационные задачи к задаче линейного программирования, заданную в допустимом каноническом виде, научиться представлять результаты расчетов в виде html-страниц.

Лабораторные занятия проводятся в компьютерных классах.

Теоретическая часть

Основным методом решения задач линейного программирования является симплекс-метод. Геометрический смысл симплекс-метода состоит в последовательном переходе от одной вершины многогранника решений (называемой первоначальной вершиной) к соседней, в которой функция цели принимает лучшее (по крайней мере, не худшее) значение до тех пор, пока не будет найдено оптимальное решение – вершина, в которой достигается оптимальное значение функции цели.

Cимплекс-метод можно применять в том случае, когда задача программирования задана в каноническом виде. В дальнейшем, будем рассматривать задачи линейного программирования канонического вида, так как любая ЗЛП может быть сведена к решению канонической задачи.

Задача линейного программирования имеет канонический вид, если система ограничений задана множеством уравнений:

и каждое i-е уравнение содержит переменную такую, что коэффициент перед ним в этом уравнении равен 1, а во всех других уравнениях равен 0. Если при этом , то говорят о допустимом каноническом виде. Переменные называют базисными, остальные – свободными.

ЗЛП допустимого канонического вида может быть записана в допустимой симплекс-таблице следующего вида: левый крайний столбец содержит номера базисных переменных, верхняя строка – номера свободных переменных. В точке пересечения строки, соответствующей значению , и столбца, соответствующего , стоит коэффициент при свободной переменной в уравнении i, в котором выделена базисная переменная . Соответственно, справа записаны постоянные члены уравнений, внизу – коэффициенты целевой функции от свободных переменных, а в правом нижнем углу записано значение «-Q₀».

Симплекс-таблица

		…
		…
…	…		…	…
		…
		…

Допустимому каноническому виду ЗЛП или соответствующей допустимой симплекс-таблице сопоставляется точка , , , . Координаты этой точки удовлетворяют n линейно-независимым условиям ЗЛП: m уравнениям и n-m неравенствам для свободных переменных. Эта точка является допустимым базисным решением и вершиной многогранника решений.

Допустимой симплекс-таблице соответствует точка минимума, если все коэффициенты целевой функции неотрицательны:

, …,

Тогда минимальное значение целевой функции равно

Если критерий не выполнен, то есть не все коэффициенты целевой функции неотрицательны, то следует перейти от одного допустимого решения к соседнему допустимому, то есть такому, в котором множества базисных и свободных переменных изменены на один элемент. Этот процесс называют симплекс-шагом или заменой базиса. Опишем последовательно его этапы.

1) Выбор разрешающего столбца: среди элементов последней строки таблицы выбирается любой , и соответствующий столбец называется разрешающим. В качестве рекомендуется выбирать минимальное .

2) Выбор разрешающей строки: если для всех элементов разрешающего столбца, то минимум не существует. Если это не так, то для всех положительных вычислим отношение . Строка i, для которой отношение минимально, называется разрешающей строкой , общий элемент разрешающего столбца и разрешающей строки называется разрешающим элементом.

3) Замена базиса при помощи разрешающего элемента . Если w – какое-либо значение в таблице, то через будем обозначать значение, стоящее в новой таблице на том же самом месте:

а)номера переменных из разрешающей строки и разрешающего столбца меняются местами,	, ,
номера других переменных остаются на месте	для всех , для всех ;
б) разрешающий элемент заменяется на обратное значение:	,

остальные элементы разрешающего столбца и разрешающей строки делят на разрешающий элемент со знаком «-» для элементов разрешающего столбца и со знаком «+» для элементов разрешающей строки, то есть

элементы разрешающего столбца заменяются следующим образом: для всех ,	;
и элементы разрешающей строки заменяются следующим образом: для всех ,	;

в) элементы симплекс-таблицы, не принадлежащие разрешающей строке и разрешающему столбцу, пересчитываются следующим образом - из элемента вычитается произведение соответствующих элементов из разрешающей строки и разрешающего столбца, деленное на разрешающий элемент:

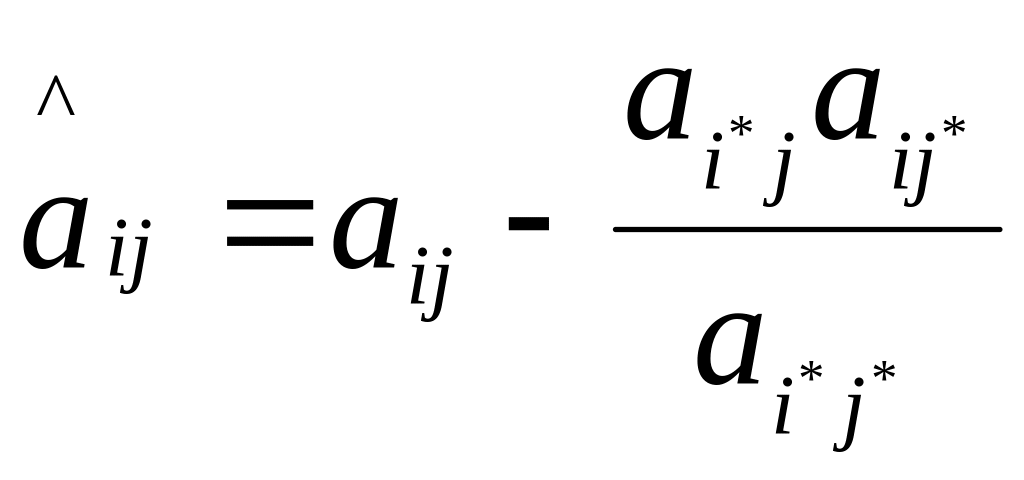для всех и ,

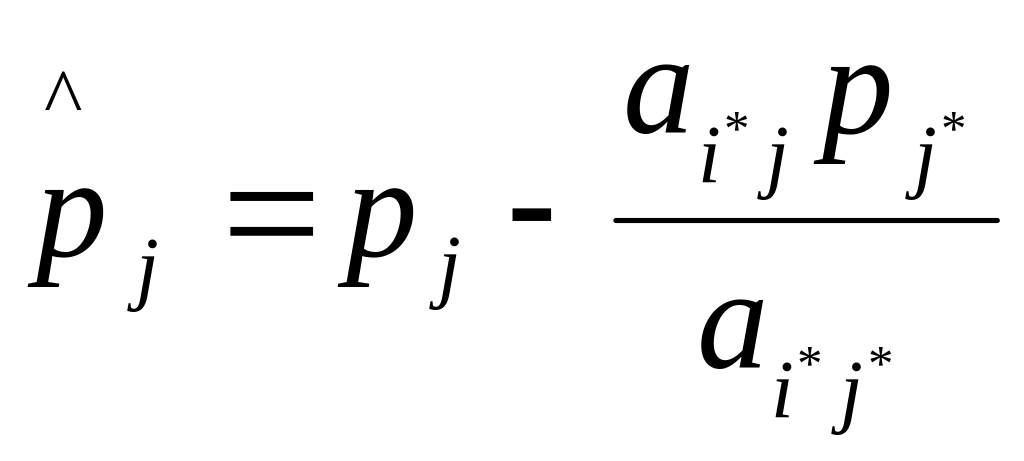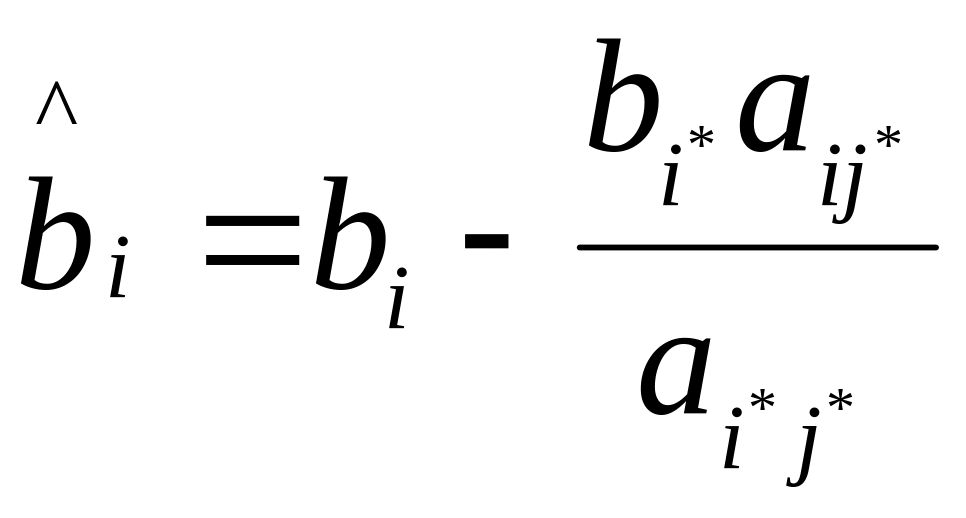для всех ,

для всех ,

.

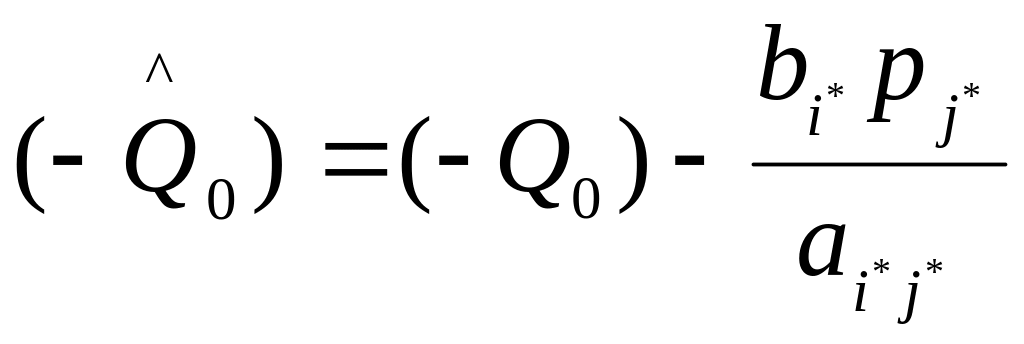Всегда должно получаться и . Может случиться, что , хотя . После пересчета всех элементов симплекс-таблицы проверяется критерий минимальности - все коэффициенты целевой функции должны быть неотрицательны.

Отметим, что переменным, индекс которых стоит в верхней строке, в базисном решении приписывается значение 0; это свободные переменные. Каждая из переменных, индекс которых стоит в левом столбце, приравнивается к числу, записанному в правом столбце той же самой строки; это базисные переменные.

В MatLab задача линейного программирования решается с помощью функции Linprog:

Синтаксис:

Различные варианты записи правой части вызова функции Linprog:

x = linprog(f,A,b,Aeq,beq)

x = linprog(f,A,b,Aeq,beq,lb,ub)

[x,fval] = linprog(...)

[x,fval,exitflag] = linprog(...)

[x,fval,exitflag,output] = linprog(...)

Различные варианты записи левой части вызова функции Linprog:

• x = linprog(f,A,b) находит min f'*x при условии, что A*x <= b.

• x = linprog(f,A,b,Aeq,beq) решает указанные выше задачу при условии дополнительного выполнения ограничений в виде равенств Aeq*x = beq. Если нет неравенств, то устанавливается A=[] и b=[].

• x = linprog(f,A,b,Aeq,beq,lb,ub) определяет набор нижних и верхних границ для проектируемых переменных х, так что решение всегда находится в диапазоне lb <= x <= ub. Если нет неравенств, то устанавливается Aeq=[] и beq=[].

• [x,fval] = linprog(...) возвращает значение целевой функции fun как решение от х: fval = f'*x.

• [x,lambda,exitflag,output] = linprog(...) возвращает структурный выход с информацией об оптимизации

• [x,fval,exitflag,output,lambda] = linprog(...) Возвращает структурную lambda, чьи поля включают в себя множители Лагранжа как решение от х.

Для приведенного примера вызов функции имеет вид

[x,p] = linprog(f,A,b,[],[],lb);

x

p

Выходные аргументы.

exitflag	Описывает выходные условия. > 0 Данная функция сходится к решению по х 0 Максимальное число оценки функции или итерации было превышено < 0 Функция не сходится к никакому решению
lambda	Структура, которая содержит множители Лагранжа при решении по х (разделенном по типам условий). Поле структуры: lower Нижние границы lb upper Верхние границы ub ineqlin Линейные неравенства eqlin Линейные равенства
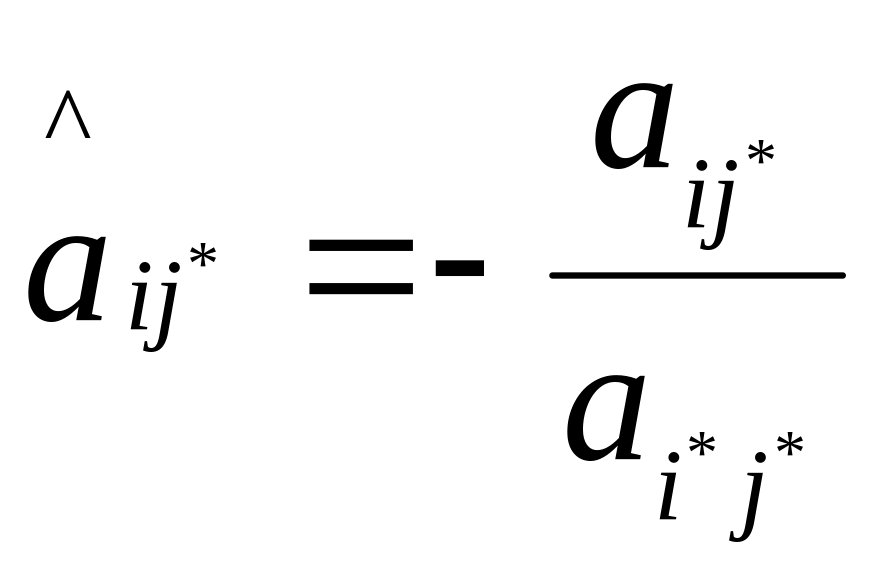
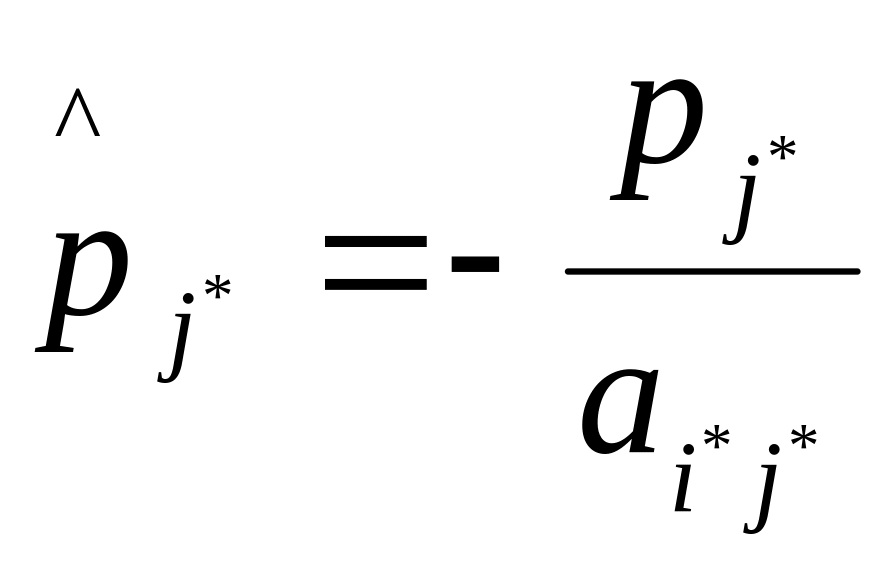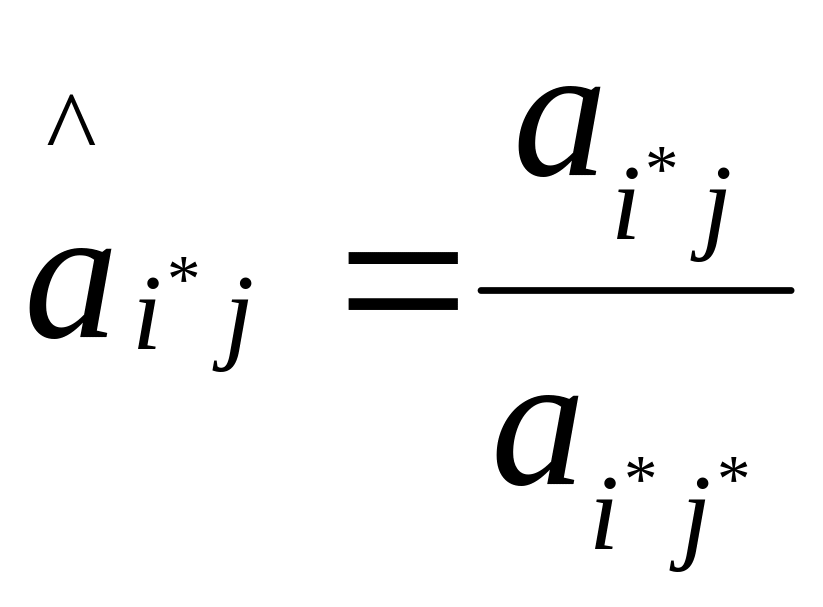
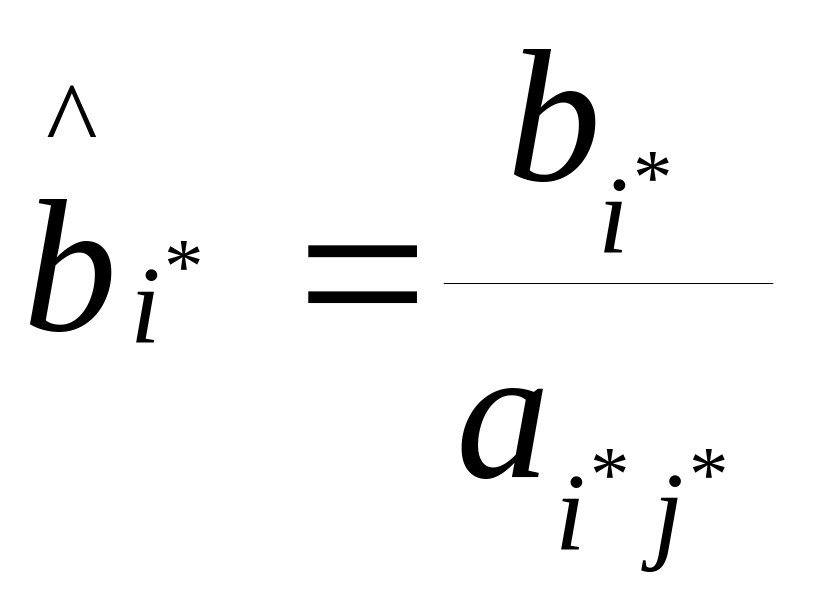output	Структура, которая содержит информацию об оптимизации. Поле структуры: iterations Число выполненных итераций algorithm Используемый алгоритм cgiterations Число PCG итераций (только для крупно-масштабного алгоритма)