Корреляция и взаимосвязь величин Корреляция (Correlation) - это статистическая взаимосвязь двух или нескольких случайных величин.
Значительная корреляция между двумя случайными величинами всегда является свидетельством существования некоторой статистической связи в данной выборке, но эта связь не обязательно должна наблюдаться для другой выборки и иметь причинно-следственную природу. Часто заманчивая простота корреляционного исследования подталкивает исследователя делать ложные интуитивные выводы о наличии причинно-следственной связи между парами признаков, в то время как коэффициенты корреляции устанавливают лишь статистические взаимосвязи. Например, рассматривая пожары в конкретном городе, можно выявить весьма высокую корреляцию между ущербом, который нанес пожар, и количеством пожарных, участвовавших в ликвидации пожара, причём эта корреляция будет положительной. Из этого, однако, не следует вывод «увеличение количества пожарных приводит к увеличению причинённого ущерба», и тем более не будет успешной попытка минимизировать ущерб от пожаров путём ликвидации пожарных бригад. В то же время, отсутствие корреляции между двумя величинами ещё не значит, что между ними нет никакой связи. Например, зависимость может иметь сложный нелинейный характер, который корреляция не выявляет.
Показатели корреляции
Параметрические показатели корреляции
Ковариация
Важной характеристикой совместного распределения двух случайных величин является ковариация (или корреляционный момент). Ковариация является совместным центральным Ковариация определяется как:
,
где — математическое ожидание.
Свойства ковариации:
Ковариация двух независимых случайных величин и равна нулю.
Абсолютная величина ковариации двух случайных величин и не превышает среднего геометрического их дисперсий: .
. </math> </center>
|frame-style = border: 1px solid rgb(200,200,200); | title-style = color: black; background-color: rgb(255,255,221); font-weight: bold; text-align: left;| content-style = color: black; background-color: white; text-align: left; | hidden=1
}}
Ковариация имеет размерность, равную произведению размерности случайных величин, то есть величина ковариации зависит от единиц измерения независимых величин. Данная особенность ковариации затрудняет её использование в целях корреляционного анализа.
Линейный коэффициент корреляции
Для устранения недостатка ковариации был введён линейный коэффициент корреляции(или коэффициент корреляции Пирсона), который разработали в 90-х годах XIX века. Коэффициент корреляции рассчитывается по формуле:
где , — среднее значение выборок.
Коэффициент корреляции изменяется в пределах от минус единицы до плюс единицы. Линейный коэффициент корреляции связан с .
Для графического представления подобной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая пара значений маркируется при помощи определенного символа. Такой график называется «диаграммой рассеяния».
Метод вычисления коэффициента корреляции зависит от вида шкалы, к которой относятся переменные. Так, для измерения переменных с интервальной и количественной шкалами необходимо использовать коэффициент корреляции Пирсона (корреляция моментовпроизведений). Если по меньшей мере одна из двух переменных имеет порядковую шкалу, либо не является нормально распределённой, необходимо использовать ранговую корреляцию Спирмена или (тау) Кендалла. В случае, когда одна из двух переменных является дихотомической, используется точечная двухрядная корреляция, а если обе переменные являются дихотомическими: четырёхполевая корреляция. Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, когда связь между ними линейна (однонаправлена).
Непараметрические показатели корреляции
Коэффициент ранговой корреляции Кендалла
Применяется для выявления взаимосвязи между количественными или качественными показателями, если их можно ранжировать. Значения показателя X выставляют в порядке возрастания и присваивают им ранги. Ранжируют значения показателя Y и рассчитывают коэффициент корреляции Кендалла:
,
где .
— суммарное число наблюдений, следующих за текущими наблюдениями с большимзначением рангов Y.
— суммарное число наблюдений, следующих за текущими наблюдениями с меньшимзначением рангов Y. (равные ранги не учитываются!)
Если исследуемые данные повторяются (имеют одинаковые ранги), то в расчетах используется скорректированный коэффициент корреляции Кендалла:
— число связанных рангов в ряду X и Y соответственно.
Коэффициент ранговой корреляции Спирмена
Степень зависимости двух случайных величин (признаков) X и Y может характеризоваться на основе анализа получаемых результатов . Каждому показателю X и Y присваивается ранг. Ранги значений X расположены в естественном порядке i=1, 2, . . ., n. Ранг Y записывается как Ri и соответствует рангу той пары (X, Y), для которой ранг X равен i. На основе полученных рангов Х i и Yi рассчитываются их разности и вычисляется коэффициент корреляции Спирмена:
Значение коэффициента меняется от -1 (последовательности рангов полностью противоположны) до +1 (последовательности рангов полностью совпадают). Нулевое значение показывает, что признаки независимы.
Коэффициент корреляции знаков Фехнера
Подсчитывается количество совпадений и несовпадений знаков отклонений значений показателей от их среднего значения.
C — число пар, у которых знаки отклонений значений от их средних совпадают.
H — число пар, у которых знаки отклонений значений от их средних не совпадают.
Коэффициент множественной ранговой корреляции (конкордации)
— число групп, которые ранжируются.
— число переменных.
— ранг -фактора у -единицы.
Значимость:
, то гипотеза об отсутствии связи отвергается.
В случае наличия связанных рангов:
Свойства коэффициента корреляции
Неравенство Коши — Буняковского:
если принять в качестве скалярного произведения двух случайных величин ковариацию , то норма случайной величины будет равна , и следствием неравенства Коши — Буняковского будет:
.
Коэффициент корреляции равен тогда и только тогда, когда и линейно зависимы (исключая события нулевой вероятности, когда несколько точек «выбиваются» из прямой, отражающей линейную зависимость случайных величин):
,
где . Более того в этом случае знаки и совпадают:
.
= a^2 \overline{X^2} + b^2 \overline{Y^2} + 2ab\overline{XY}. </math> </center> Если предположить, что коэффициент корреляции
то предыдущее выражение перепишется в виде
Поскольку всегда можно выбрать числа a и b так, чтобы (например, если , то берём произвольное a и ), то при этих a и b дисперсия , и значит почти наверное. Но это и означает линейную зависимость между X и Y. Доказательство очевидным образом обобщается на случай величин X и Y с ненулевыми средними, только в вышеприведённых выкладках надо будет X заменить на , и Y — на .
|frame-style = border: 1px solid rgb(200,200,200); | title-style = color: black; background-color: rgb(255,255,221); font-weight: bold; text-align: left;| content-style = color: black; background-color: white; text-align: left; | hidden=1
}}
Если \R_{X,Y} = 0</math>. Обратное в общем случае неверно.
Корреляционный анализ
Корреляционный анализ — метод обработки
Ограничения корреляционного анализа
Применение возможно при наличии достаточного количества наблюдений для изучения. На практике считается, что число наблюдений должно не менее чем в 5-6 раз превышать число факторов (также встречается рекомендация использовать пропорцию, не менее чем в 10 раз превышающую количество факторов). В случае если число наблюдений превышает количество факторов в десятки раз, в действие вступает
Необходимо, чтобы совокупность значений всех факторных и результативного признаков подчинялась .
Исходная совокупность значений должна быть качественно однородной.
Сам по себе факт корреляционной зависимости не даёт основания утверждать, что одна из переменных предшествует или является причиной изменений, или то, что переменные вообще причинно связаны между собой, а не наблюдается действие третьего фактора.
Область применения
Данный метод обработки статистических данных весьма популярен в промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие. В различных прикладных отраслях приняты разные границы интервалов для оценки тесноты и значимости связи.
Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.
В селекции
Корреляция — взаимосвязь признаков (может быть положительной или отрицательной). Обусловлена сцеплением генов или плейотропией
См. также
Автокорреляционная функция
Взаимнокорреляционная функция
Ковариация
Коэффициент детерминации
Примечания
Литература
Ссылки
Калькулятор для расчета коэффициента корреляции по Пирсону
Границы значений коэффициента корреляции
Иллюстрация: зависимые случайные величины с нулевой корреляцией
Корреляция - это один из основных терминов теории вероятности, показывающий меру зависимости между двумя и более случайными величинами. Данная зависимость выражается через коэффициент корреляции. Коэффициент корреляции принимает значения от -1 до +1. Чем выше значение коэффициента корреляции, тем больше зависимость между величинами. Корреляция бывает положительной и отрицательной.
Зависимость между величинами
Корреляция - это статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин. Математической мерой корреляции двух случайных величин служит корреляционное отношение, либо коэффициент корреляции. В случае, если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической.
Графиком прямо пропорциональной зависимости величин
Корреляция - это понятие, которым отмечают связь между явлениями, если одно из них входит в число причин, определяющих другие, или если имеются общие причины, воздействующие на эти явления (функция является частным случаем корреляции); кореляция может быть более или менее тесной (т.е. зависимость одной величины от другой - более или менее ясно выраженной); число, показывающее степень тесноты корреляции, называется коэффициентом корреляции (это число заключено между -1 и 1).
Графиком обратно пропорциональной зависимости величин
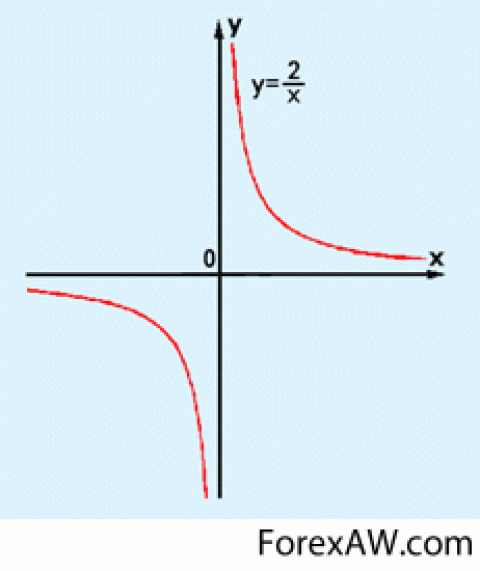
Смотреть видео 1, добавленное в раздел "Корреляция - это, определение"
Корреляция - это взаимная связь явлений, находящихся в известной зависимости друг от друга. Рост безработицы и количество уголовных преступлений находятся в прямой корреляции друг к другу.
График зависимости проекции скорости от времени для тела, движущегося вдоль оси времени
Корреляция - это степень зависимости между двумя переменными. Линейная корреляция между двумя переменными х и у определяется знаком и величиной. Между двумя переменными существует положительная корреляция, если данная сумма положительна, и отрицательная корреляция, если сумма отрицательна. Степень корреляции измеряется коэффициентом корреляции r, который меняется от +1 до –1, достигая значения +1, когда х и у полностью положительно коррелируются между собой, и –1, когда х и у полностью отрицательно коррелируются между собой; если r = 0, х и у являются независимыми переменными. r не зависит от единиц измерения х и у.
График зависимости проекции ускорения от времени
Корреляция - это вероятностная или статистическая зависимость. В отличие от функциональной зависимости корреляция возникает тогда, когда зависимость одного из признаков от другого осложняется наличием ряда случайных факторов.
Путь, пройденный телом, численно равен площади под графиком функции
Корреляция - это статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения одной или нескольких из этих величин приводят к систематическому изменению другой или других величин. Мерой корреляции двух случайных величин служит коэффициент корреляции.
Зависимость проекции перемещения от времени для тела
Смотреть видео 2, добавленное в раздел "Корреляция - это, определение"
Коэффициент корреляции - это математическая мера корреляции двух величин. Коэффициенты корреляции могут быть положительными и отрицательными. Если при увеличении значения одной величины происходит уменьшение значений другой величины, то их коэффициент корреляции отрицательный. В случае, когда увеличение значений первого объекта наблюдения приводит к увеличениям значения второго объекта, то можно говорить о положительном коэффициенте. Возможна еще одна ситуация отсутствия статистической взаимосвязи - например, для независимых случайных величин.
Полная положительная корреляция
Коэффициент корреляции - это мера выражения тенденции роста одной переменной при увеличении другой. Его значения всегда находятся внутри диапазона -1; +1. Чем ближе значение переменной к -1 или 1, тем значительнее коррелируют между собой исследуемые величины. При К=0 можно говорить о полном отсутствии корреляции между наблюдаемыми величинами. Если К=-1 или К=1, то говорят уже о функциональной зависимости величин.
Полная отрицательная корреляция
Коэффициент корреляции или парный коэффициент корреляции в теории вероятностей и статистике - это мера линейной зависимости двух случайных величин.
Визуализация различных значений коэффициента корреляции
Коэффициент корреляции - это статистическая мера направления и степени линейной зависимости между двумя случайными переменными (меняется от -1 до +1).
Корреляция количества нобелевских лауреатов от количества магазинов Икея
Коэффициент корреляции - это величина, характеризующая направление и силу связи между признаками. Коэффициент корреляции, который одним числом дает представление о направлении и силе связи между признаками (явлениями), пределы его колебаний от 0 до + - 1.
Корреляция среднего количества однополых сексуальных партнеров от интеллекта
Коэффициент корреляции - это статистический показатель, показывающий, насколько связаны между собой колебания значений двух других показателей. Например, насколько движение доходности ПИФа связано, перекликается (коррелирует) с движением индекса, выбранного для расчета коэффициента бета для этого ПИФа. Чем ближе значение коэффициента корреляции к 1, тем больше коррелируют ПИФ и индекс, а значит коэффициент бета и, следовательно, коэффициент альфа можно принимать к рассмотрению. Если значение этого коэффициента корреляции меньше 0,75, то указанные показатели бессмысленны.
Корреляция религиозности от интеллекта
Коэффициент корреляции - это величина, которая может варьировать в пределах от +1 до -1. В случае полной положительной корреляции этот коэффициент равен плюс 1, а при полной отрицательной - минус 1.
Корреляция количества пиратов и глобального потепления
|
