Лекція 6. Поняття про теорію спадкової повзучості

Згідно сучасних уявлень, напруження, що виникають у реальних тілах, складаються з двох частин: перша складова залежить від деформації в даний момент часу t, друга – від деформацій, що існували в тілі протягом часу, що передував справжньому моменту часу – . Час змінює структуру.

Теорія, що дозволяє визначати деформації в середовищі з ураху-ванням історії її навантаження, називається теорією спадкової повзучості.

Т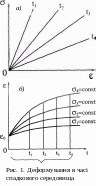 еорія спадкової зміни внутрішніх чинників з урахуванням «пам'яті» ма-теріалу про всі тимчасові структурні зміни, що виникають у процесі наван-таження, і допускаюча лінійну залеж-ність між напруженнями і деформація-ми у будь-який момент часу, одержала назву теорії лінійної спадкової повзу-чості.

Теорія лінійної спадковості була запропонована Л. Больцманом з вико-ристанням математичного апарату ін-тегральних рівнянь В. Вольтера.

Відповідно до цієї теорії, дефор-мації середовища під дією зовнішніх сил продовжуються і після їх прик-ладання (спадковість), при цьому де-формації в кожен момент часу прямо пропорційні діючим у різні моменти часу напруженням (лінійність) суму-ються, ростуть у часі (принцип суперпозиції).

Проілюструємо вище викладене на наступному прикладі. Побу-дуємо криві повзучості =f(t, ) при різних рівнях напруження (рис. 1, а). Потім в координатах « - » побудуємо графіки в моменти часу t_i (і=1,2,3...) (рис. 1, б). Якщо ізохорні залежності, що вийшли при цьому, є прямими лініями (або близькими до них), то ми маємо справу з лінійним спадковим середовищем.

Повзучість матеріалів в теорії лінійної спадковості описується інтегральним рівнянням Вольтера другого роду:

(1)

де (t) і γ(t) – напруження і деформації в даний момент часу t, t – час, який передує моменту часу t; L(t) – деяка функція, яка враховує вплив часу на деформації і напруження в тілі.

При із співвідношення (1) отримаємо рівняння повзучості деформацій:

(2)

Диференціюючи обидві частини рівняння (2) по часу, отримаємо вираз:

з якого слідує, що L(t) являє собою функцію швидкості повзучості. Функцію ж L(t–) називають ядром інтегрального рівняння Воль-тера (1). Розв’язуючи це відносно (t), отримаємо,

(3)

При з (3) отримаємо рівняння релаксації на-пружень:

(4)

Диференціюючи обидві частини (4) по t, отримаємо вираз для K(t):

Функції K(t) і L(t) взаємопов’язані і це дозволяє за однією з них знайти іншу. Функція K(t) називається резольвентою інтегрального рівняння Вольтера (2).

Рівняння повзучості (2) можна записати у вигляді:

де – тимчасовий оператор, який визначається у результаті оброб-ки експериментальних даних.

Ю.Н. Работнов показав, що задачу лінійної спадковості можна формально розглядати, як задачу теорії пружності, в якій замість пружних постійних Е і  необхідно використовувати їх тимчасові аналоги (інтегральні оператори) і . Ж.С. Ержанов встановив, що деформація ряду гірських порід до певного рівня навантаження відповідає рівнянню (2) з ядром повзучості у вигляді степеневої функції (ядро типу Абеля):

де  і  – реологічні характеристики, отримані експериментально.

Інтегральне рівняння повзучості з ядром Абеля має наступний розв’язок:

(5)

Складність рішення задач методами теорії спадкової повзучості полягає в розшифровці тимчасових операторів.

Часто при постійності граничних умов для вирішення задач геомеханіки використовують метод змінних модулів, який полягає у тому, що замість інтегральних операторів і використовують часові функції E(t) і (t).

З виразу (5) слідує, що функція часу модуля деформації має вигляд

де Ф – функція повзучості, яка рівна:

Функція часу для коефіцієнта Пуассона визначається за формулою:

Слід відмітити, що використання теорії спадкової повзучості виправдане тільки в тому випадку, коли діюче напруження не перевищує тривалої міцності масиву.