Завдання для перевірки знань

1. Знайти матрицю А= ( 2В – 3С)D

В = , С = , D =

2. Знайти значення і .

А = , В = .

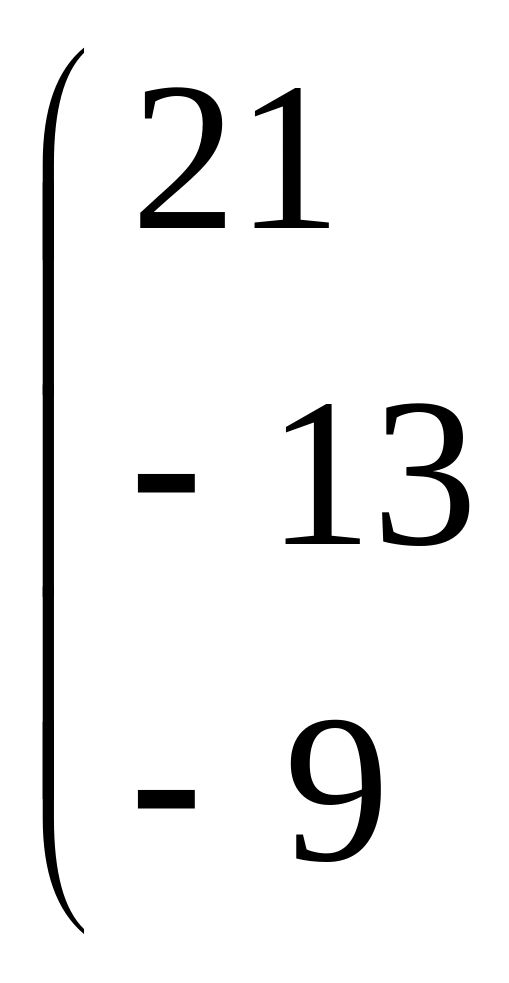
Відповідь: f (A) = ; f (B) = .

0. Обернені матриці. Елементарні перетворення. Ранг матриці.

Квадратна матриця порядку

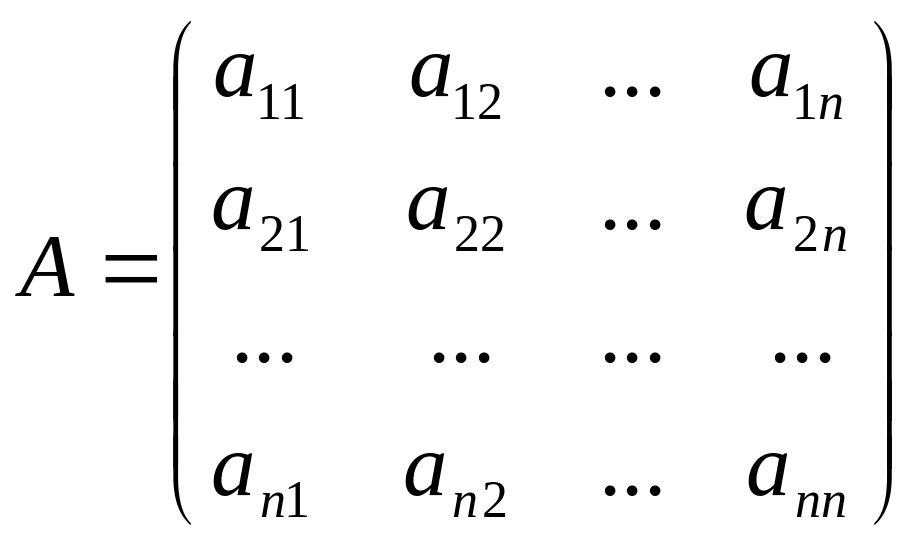(1.7)

називається невиродженою, якщо її визначник (детермінант)

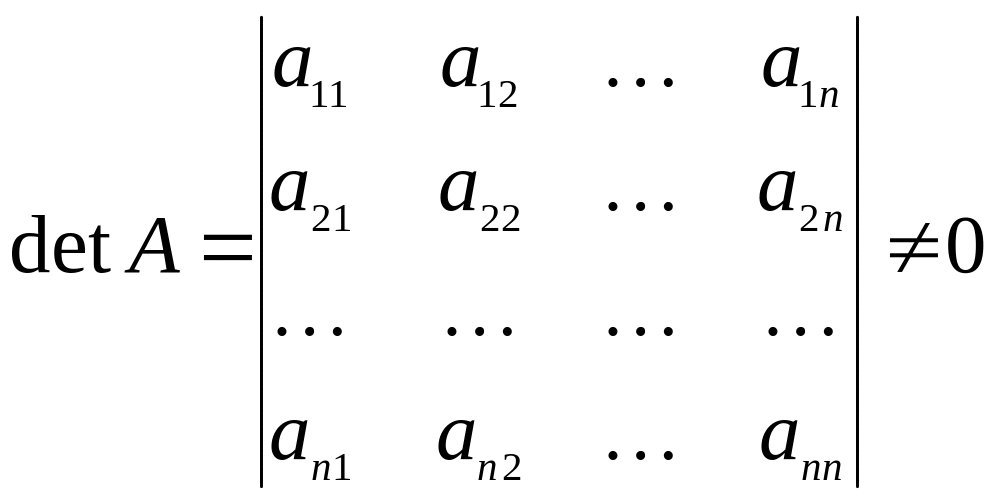
(1.8)

У випадку, коли , матриця називається виродженою.

Тільки для квадратних невироджених матриць вводиться поняття оберненої матриці [11].

Означення 1. Нехай − квадратна матриця. Матриця називається оберненою до матриці , якщо виконується умова , де - одинична матриця порядку :

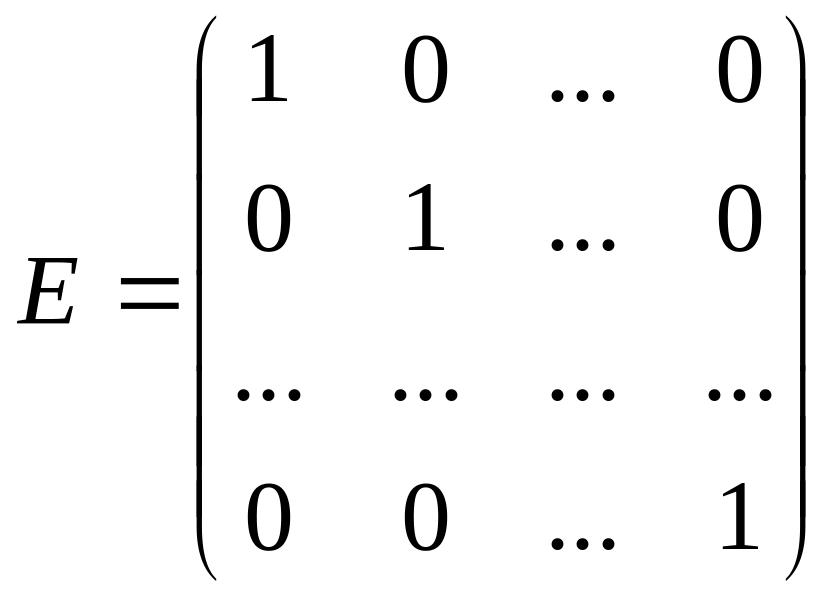(1.9)

Теорема про обернену матрицю. Для існування оберненої матриці необхідно і достатньо, щоб матриця була невиродженою. Тоді

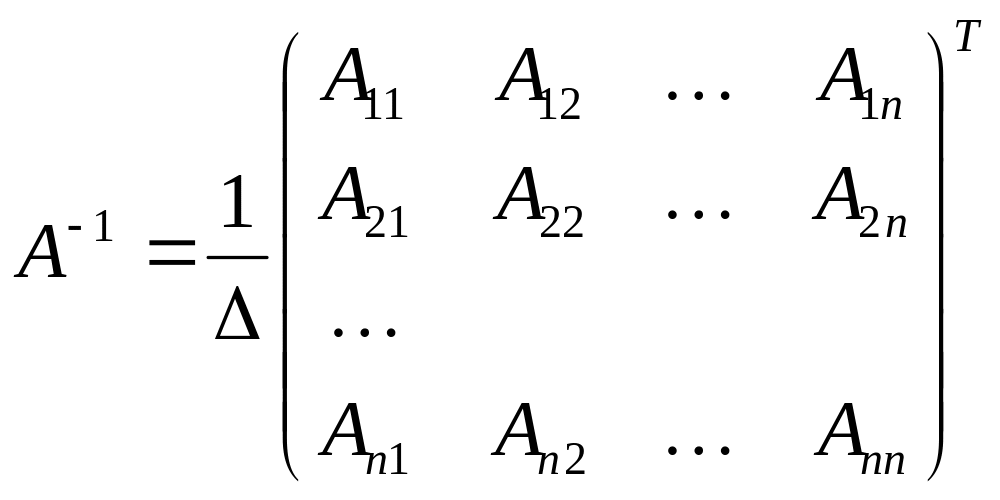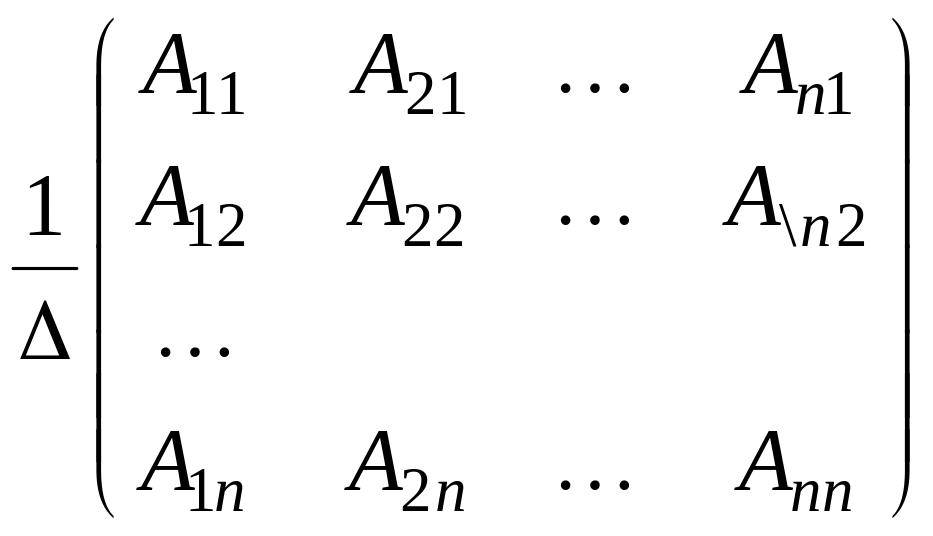= , (1.10)

де − алгебраїчні доповнення елементів матриці

.

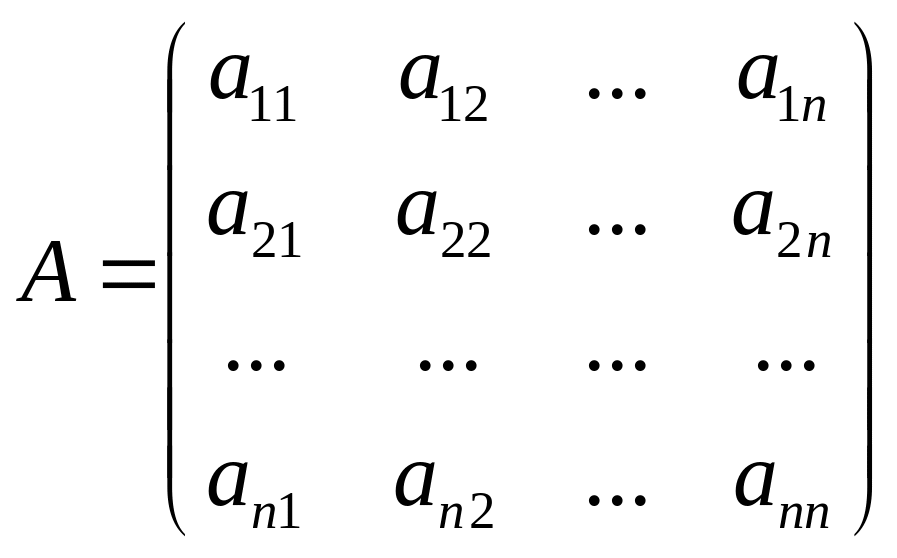Приклад 7. Задано матрицю . Переконатися, що вона не є виродженою, знайти обернену їй матрицю і перевірити виконання рівності , якщо:

а) ; б) .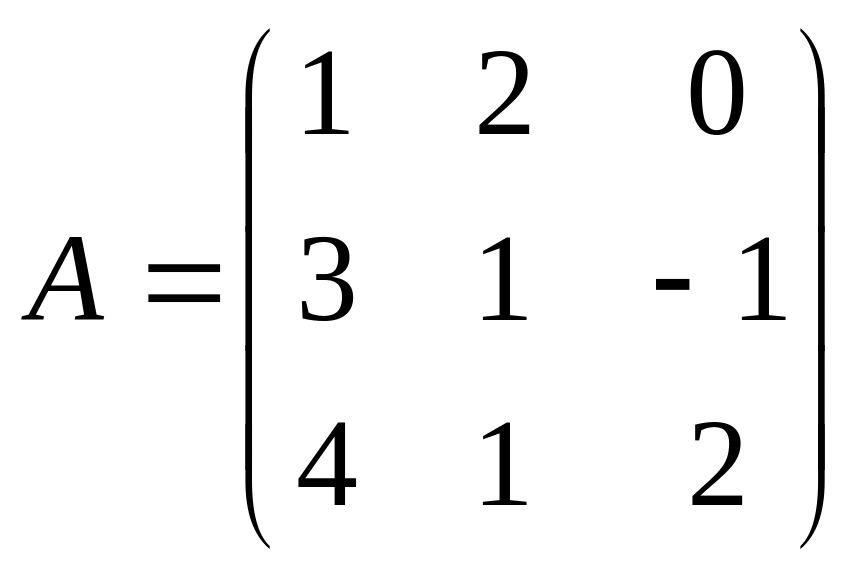

Розв’язання. а) Маємо . Далі знаходимо алгебраїчні доповнення:

Отже,

;

б) Знайдемо 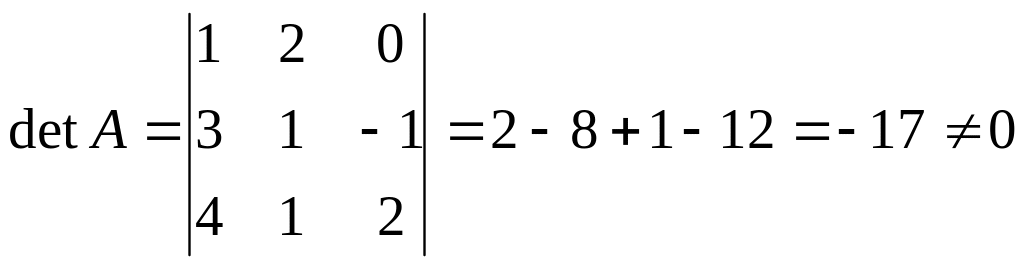, тобто матриця А – невироджена, і, значить, існує матриця А^-1. Знаходимо алгебраїчні доповнення:

Отримані значення підставляємо в формулу:

.

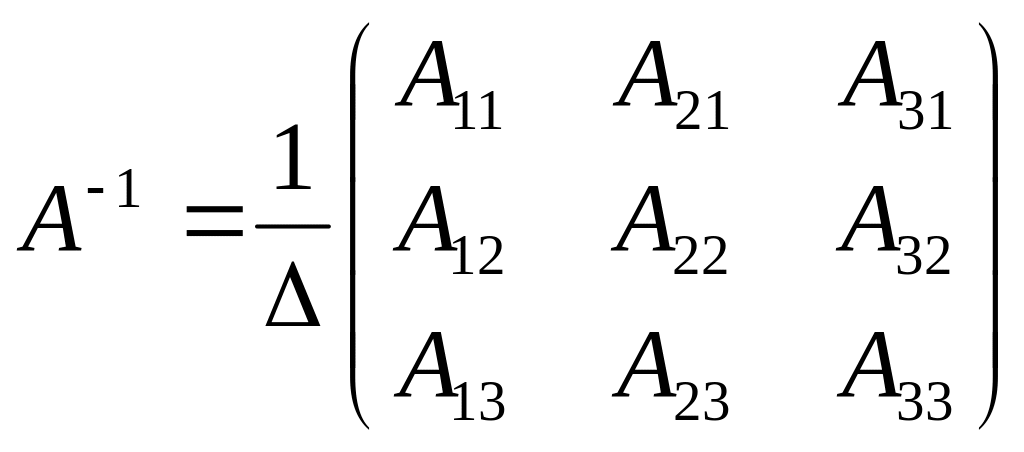Тоді

, .

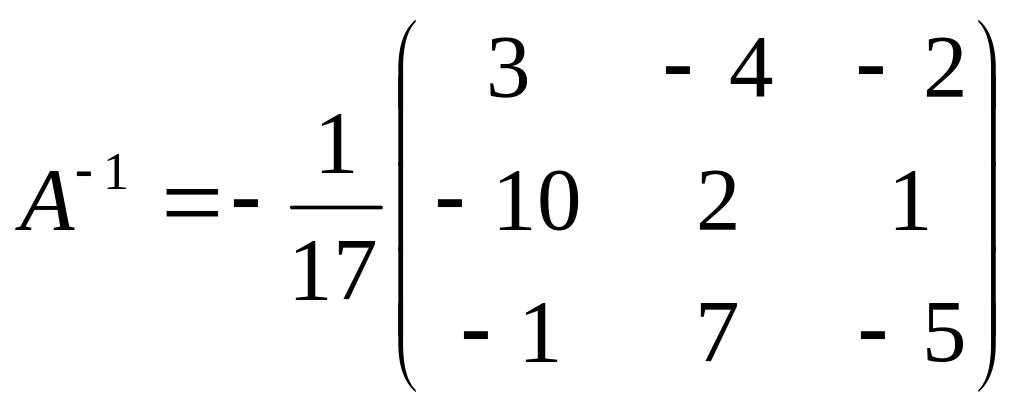Основна характеристика матриці – її ранг.

Означення 2. Рангом матриці називають порядок найбільшого відмінного від нуля мінора матриці.

Зручнішим у порівнянні зі звичайним перебором значень мінорів є метод знаходження рангу, який грунтується на тому, що ранг матриці не змінюється, якщо над матрицею виконати так звані елементарні перетворення, а саме:

1. переставити місцями два рядки (стовпці);

2. помножити кожен елемент рядка (стовпця) на один і той самий відмінний від нуля множник;

3. додати до елементів рядка (стовпця) відповідні елементи другого рядка (стовпця), помножені на одне і те саме число.

Дві матриці називаються еквівалентними, якщо одна матриця отримується з іншої за допомогою елементарних перетворень. Еквівалентність матриць і позначається ~ .

Приклад 8. 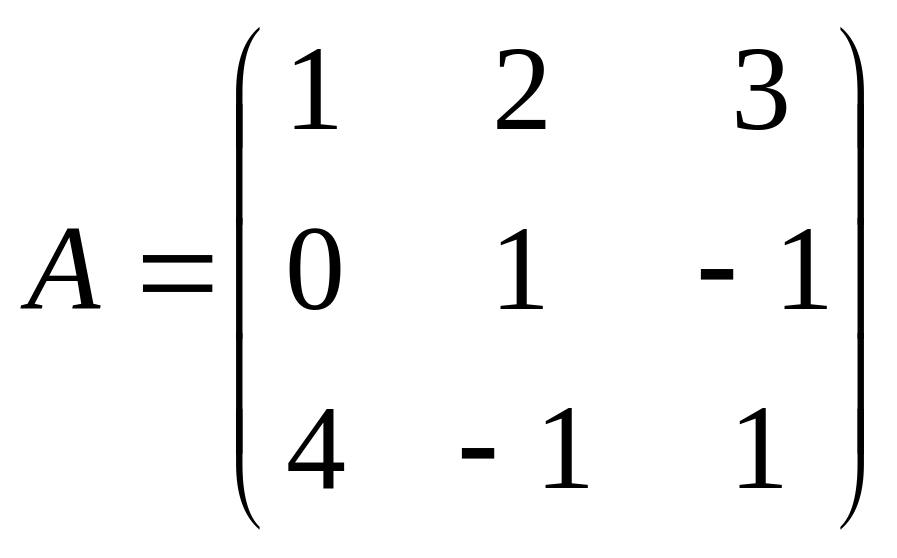. Знайти .

Розв’язання. Зведемо матрицю до еквівалентної трикутної матриці:

~ ~

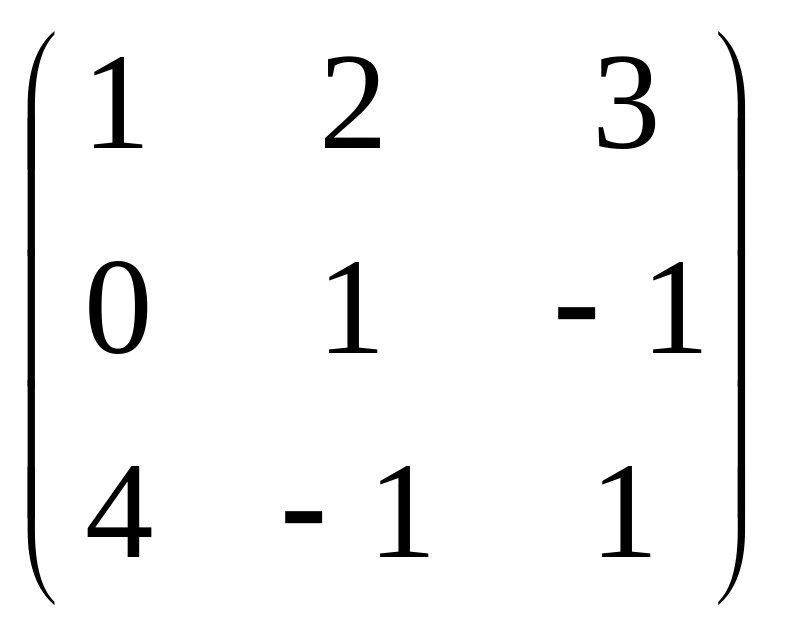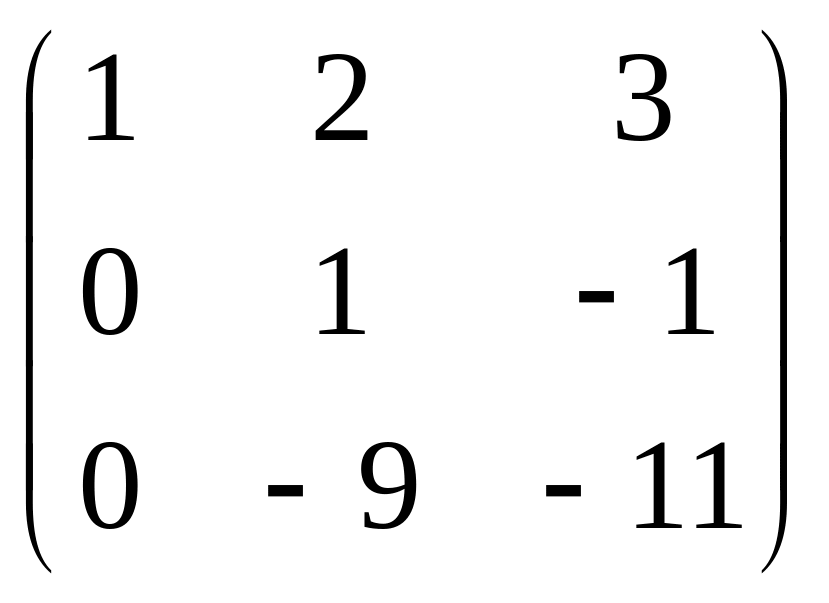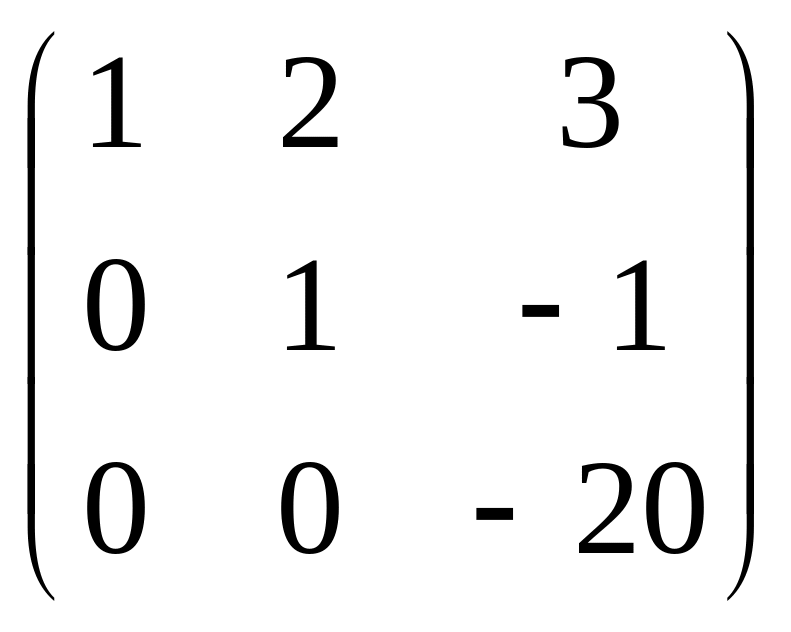
окрім мінорів 1 та 2 порядку є мінор 3 порядку . Отже .

Розглянемо ще один із методів знаходження рангу матриці.

Метод одиниць і нулів. За допомогою елементарних перетворень будь-яку матрицю можна звести до вигляду, коли кожний її рядок буде складатися тільки з нулів або із нулів і однієї одиниці. Тоді кількість одиниць, що лишилася і визначає ранг заданої матриці, оскільки отримана матриця буде еквівалентна заданій.

Приклад 9. Знайти ранг матриці

.

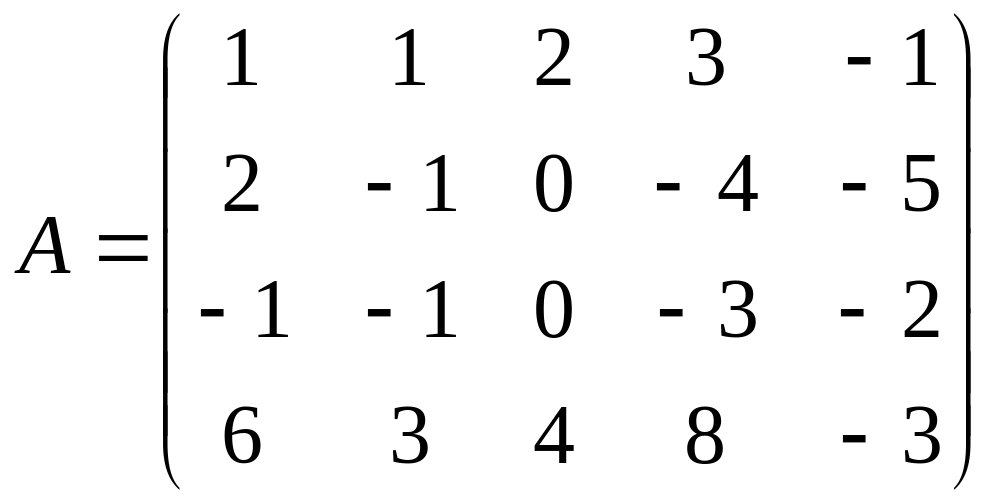Розв’язання. Домножимо третій стовпчик матриці на . Далі, отриманий перший рядок помножимо на 2 і віднімемо його від четвертого рядка. Тепер третій стовпчик містить три нулі і одиницю (в першому рядку). Легко робимо нулі в першому рядку на першій, другій, четвертій і п’ятій позиціях. Маємо:

~ .

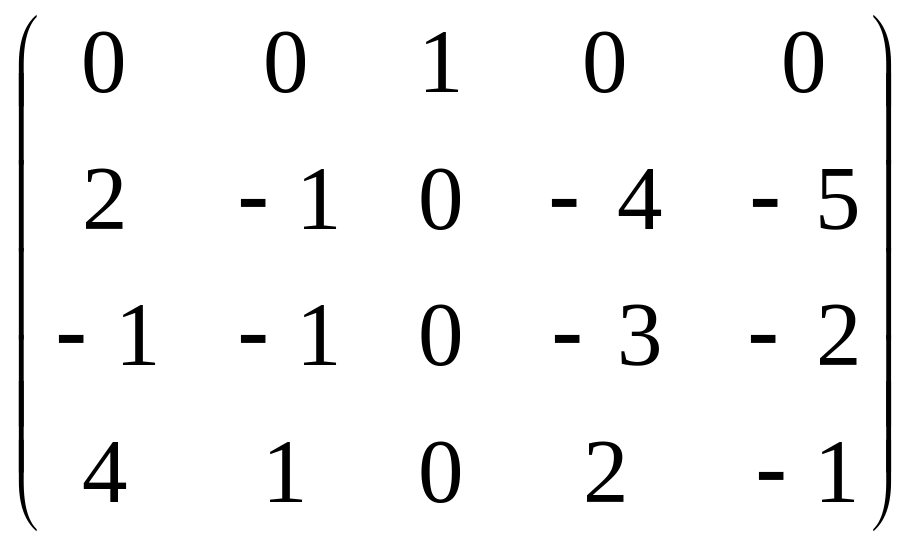Тепер четвертий рядок останньої матриці додаємо до другого і третього, отримуючи при цьому ще два нулі в другому стовпчику, після чого робимо нулі в четвертому рядку всюди, крім одиниці на перетині четвертого рядка і другого стовпця. В результаті цих елементарних перетворень отримали:

~ ~ .

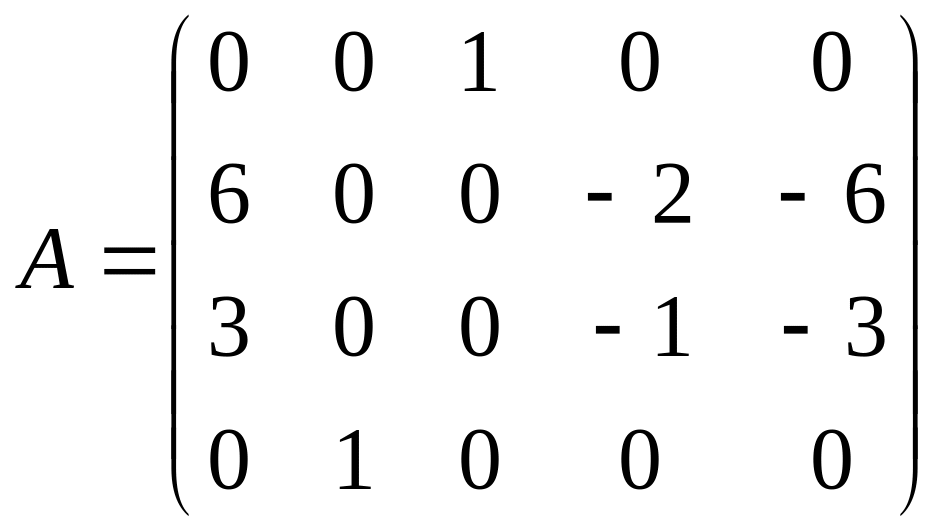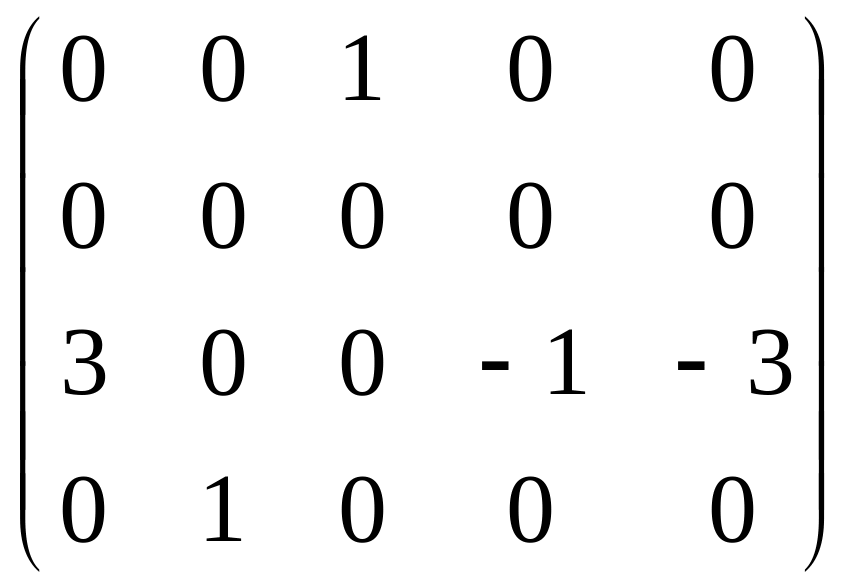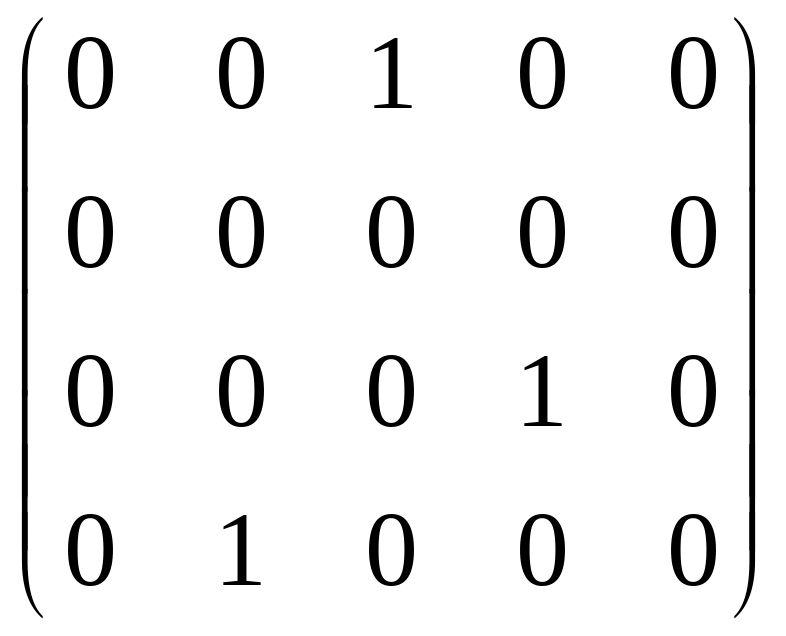Отримали три одиниці. Отже, .