
- •Матриці та їх визначники системи лінійних алгебраїчних рівнянь
- •1.1. Визначники та їх властивості. Обчислення визначників
- •Завдання для перевірки знань
- •1.2. Матриці і операції над ними
- •Завдання для перевірки знань
- •Обернені матриці. Елементарні перетворення. Ранг матриці.
- •Завдання для перевірки знань
- •1.4. Системи лінійних алгебраїчних рівнянь і методи їх розв’язання. Теорема Кронекера1)-Капеллі2)
- •Метод послідовного виключення Гаусса1).
- •Завдання для перевірки знань
- •1.5. Квадратичні форми. Приведення квадратичної форми до канонічного вигляду поворотами.
- •Завдання для перевірки знань
Розділ I
Матриці та їх визначники системи лінійних алгебраїчних рівнянь
1.1. Визначники та їх властивості. Обчислення визначників
Визначником
![]() -го
порядку
або
детермінантом
(від
лат.
determino
− визначаю)
називається число
-го
порядку
або
детермінантом
(від
лат.
determino
− визначаю)
називається число
![]() ,
яке відповідає квадратній таблиці
(відповідну матрицю, див. пункт 1.2,
записують в круглих дужках):
,
яке відповідає квадратній таблиці
(відповідну матрицю, див. пункт 1.2,
записують в круглих дужках):
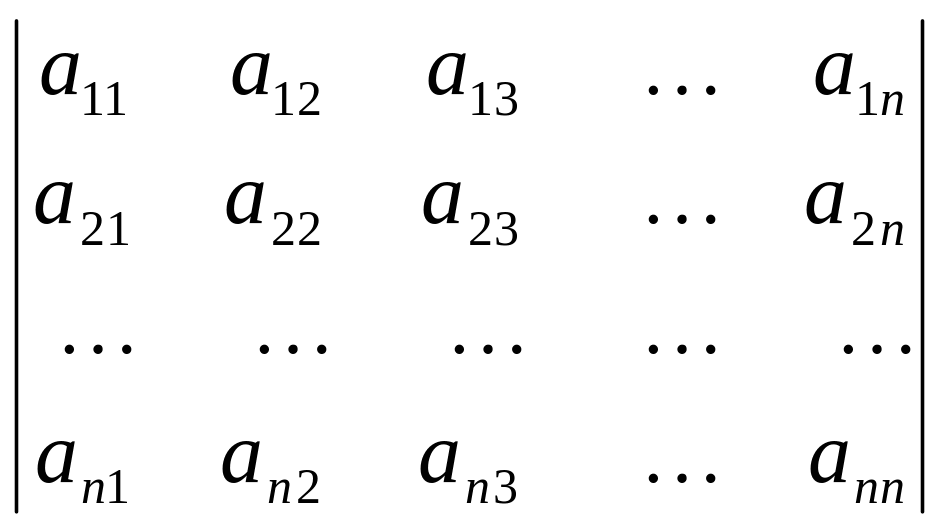 (1.1)
(1.1)
і
обчислюється згідно вказаному нижче
правилу за числами
![]()
![]() ,
які називаються елементами визначника
(всього їх
,
які називаються елементами визначника
(всього їх
![]() ).
Індекс
).
Індекс
![]() вказує на номер рядка, а
вказує на номер рядка, а
![]() -
номер стовпця квадратної таблиці (1.1),
на перетині яких знаходиться елемент
.
-
номер стовпця квадратної таблиці (1.1),
на перетині яких знаходиться елемент
.
Головною
діагоналлю визначника називається
сукупність елементів
![]()
Мінором
![]() елемента
квадратної матриці (1.1)
називають визначник
елемента
квадратної матриці (1.1)
називають визначник
![]() -го
порядку
-го
порядку
![]() ,
отриманий з визначника
,
отриманий з визначника
![]() го
порядку
викреслюванням
-го
рядка та
-го
стовпця.
го
порядку
викреслюванням
-го
рядка та
-го
стовпця.
Алгебраїчне
доповнення
![]() елемента
визначається рівністю
елемента
визначається рівністю
![]() .
.
Для
![]()
![]() .
(1.2)
.
(1.2)
Узагальнимо
правило обчислення визначника на більшу
кількість елементів, тобто на визначники
матриць більшого порядку. Нехай
![]() .
Для
обчислення таких визначників можна
скористатись методом діагоналей.
.
Для
обчислення таких визначників можна
скористатись методом діагоналей.
Метод
діагоналей (правило Саррюса):
визначник матриці дорівнює сумі добутків
елементів головних діагоналей мінус
сума добутків елементів побічних
діагоналей. Наприклад, правило Саррюса
обчислення визначника
![]() (буде рівносильним відомому правилу
трикутника) має вигляд:
(буде рівносильним відомому правилу
трикутника) має вигляд:
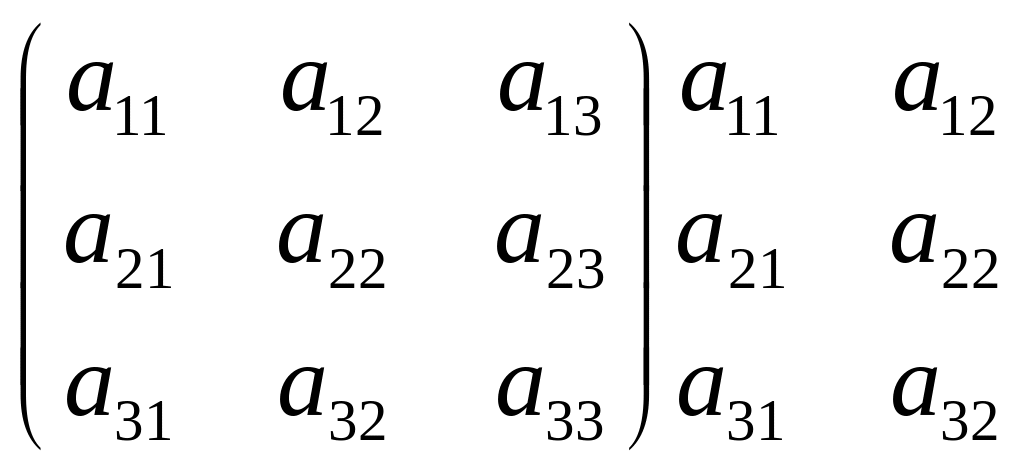


- - - + + +
У відповідності з цією схемою маємо:
![]() (1.3)
(1.3)
Приклад 1.
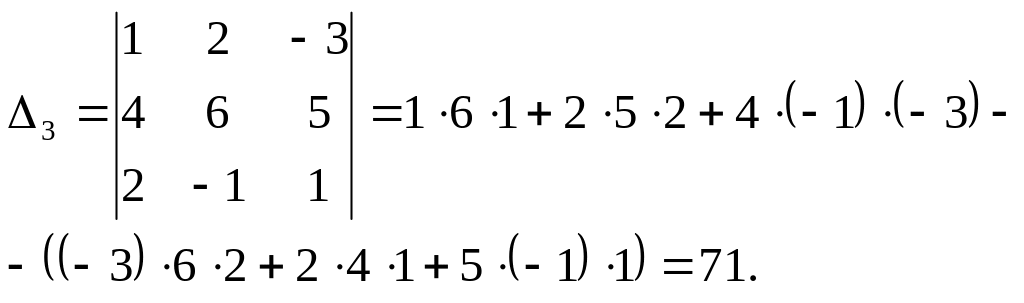
Метод розкладання: Визначник дорівнює сумі добутків елементів рядка (стовпця) на їхні алгебраїчні доповнення. Наприклад, для першого рядка маємо:
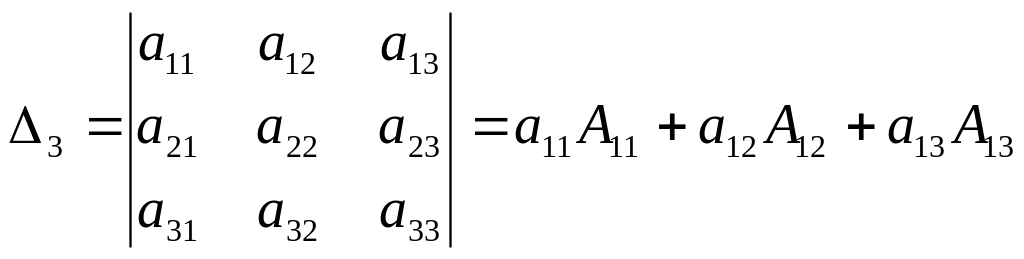 ,
(1.4)
,
(1.4)
де
![]()
![]()
![]()
Величини
![]() - алгебраїчні доповнення, а
- алгебраїчні доповнення, а
![]() -
мінори визначника
,
що відповідають його елементам
-
мінори визначника
,
що відповідають його елементам
![]() .
Ці мінори є визначниками другого порядку
і отримані із визначника
викресленням відповідних рядка і
стовпця.
Наприклад,
щоб знайти мінор
.
Ці мінори є визначниками другого порядку
і отримані із визначника
викресленням відповідних рядка і
стовпця.
Наприклад,
щоб знайти мінор
![]() ,
слід у визначнику
,
слід у визначнику
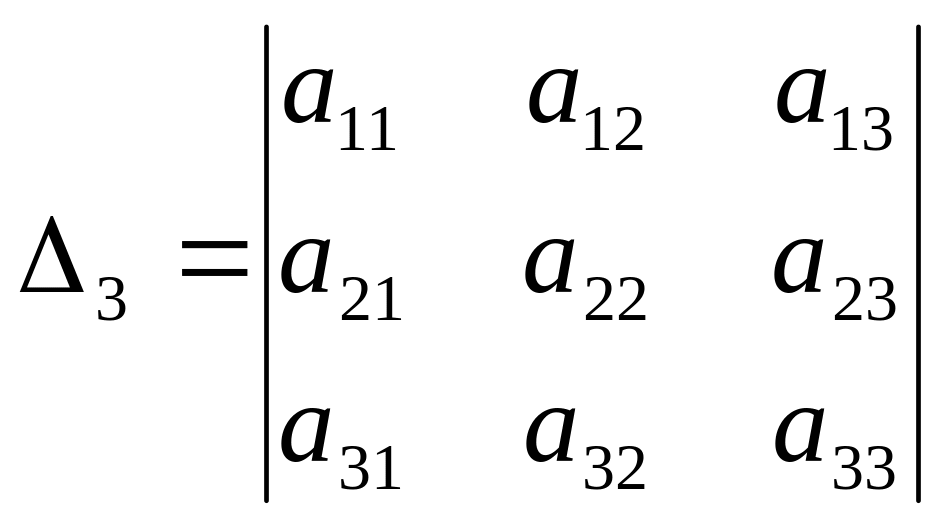 викреслити другий рядок
і
третій стовпчик.
викреслити другий рядок
і
третій стовпчик.
Одержуємо:
![]() .
.
Для
довільного
маємо таку загальну формулу для
розкладання за
![]() -м
рядком:
-м
рядком:
![]() , (1.5)
, (1.5)
де
![]() ,
а мінори
,
а мінори
![]() є визначниками
є визначниками
![]() -го
порядку, які одержуються із
викресленням першого рядка і
-го
порядку, які одержуються із
викресленням першого рядка і
![]() -го
стовпця.
-го
стовпця.
Наприклад,
для розкладання за 1-м рядком, маємо:
![]() =
=![]() ;
;
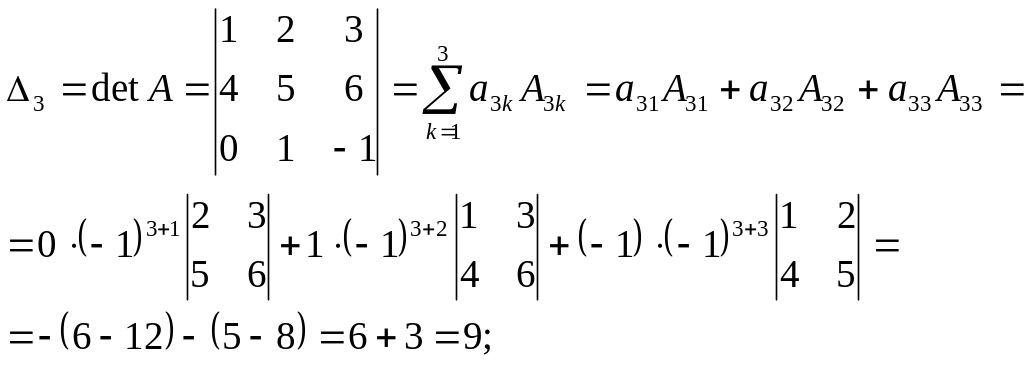
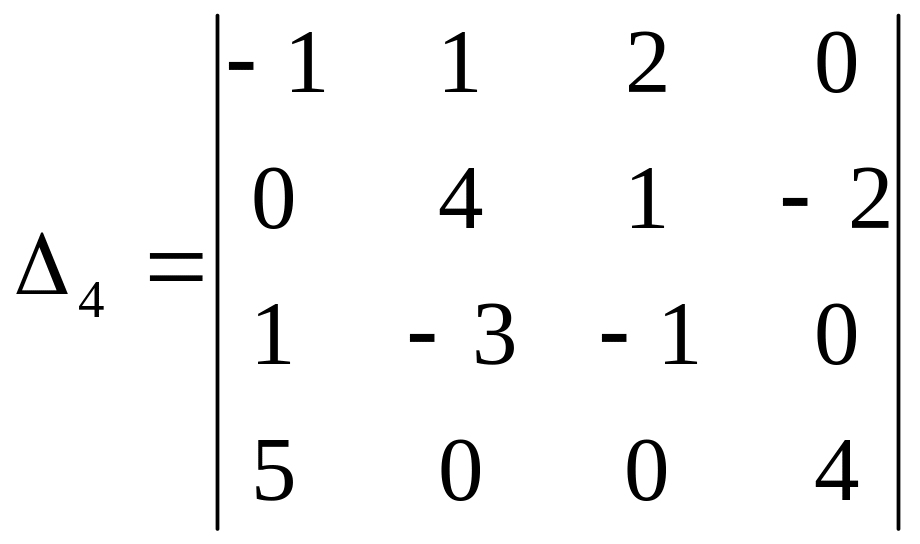 =
=
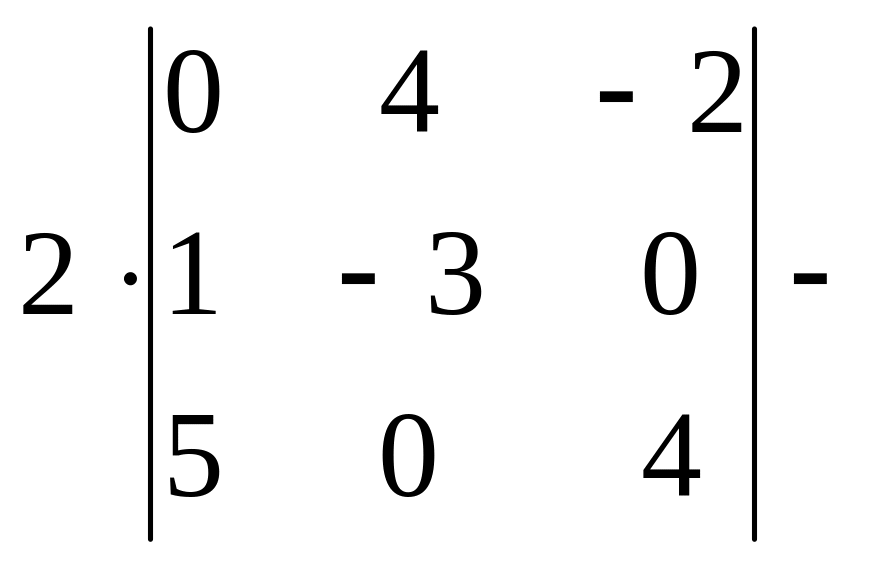
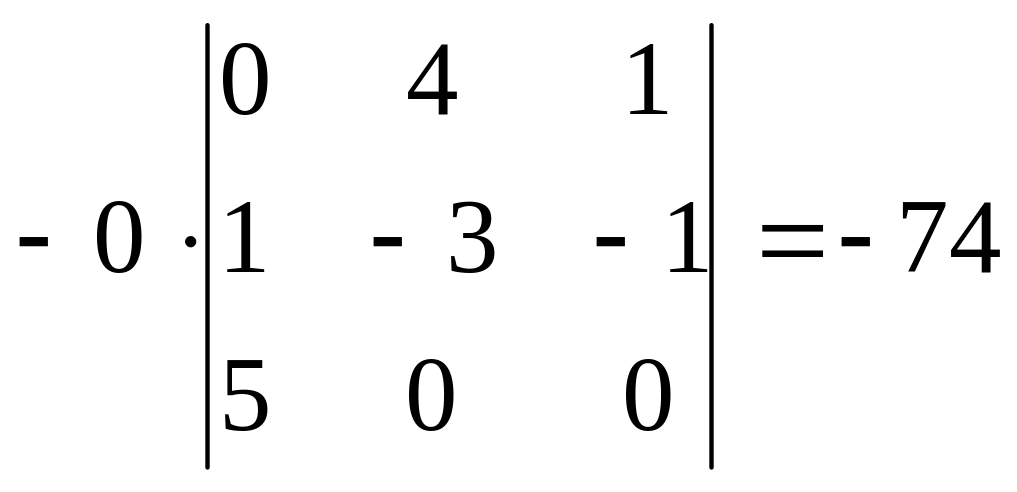 .
.
Відповідна
формула для розкладання за довільним
![]() -м
стовпчиком має вигляд:
-м
стовпчиком має вигляд:
![]() .
.
Зауваження 1. Метод розкладання дає можливість обчислювати визначники довільного порядку. Так, наприклад, визначник четвертого порядку зводиться до обчислення чотирьох визначників третього порядку, визначник п’ятого порядку – до обчислення п’яти визначників четвертого порядку, тобто – двадцяти визначників третього порядку і т. д. Такий спосіб обчислення визначників вищих порядків громіздкий, тому іноді доцільніше користуватися іншими методами обчислення визначників.
Зауваження 2. Якщо елементами визначника є деякі функції, то даний визначник – також функція.
Наприклад,
![]()
![]()
![]()
Можна показати, що для визначника будь-якого порядку мають місце наступні властивості:
1. Визначник не зміниться, якщо його рядки замінити відповідними стовпцями.
Доведення.
Для
випадку
![]() маємо:
маємо:
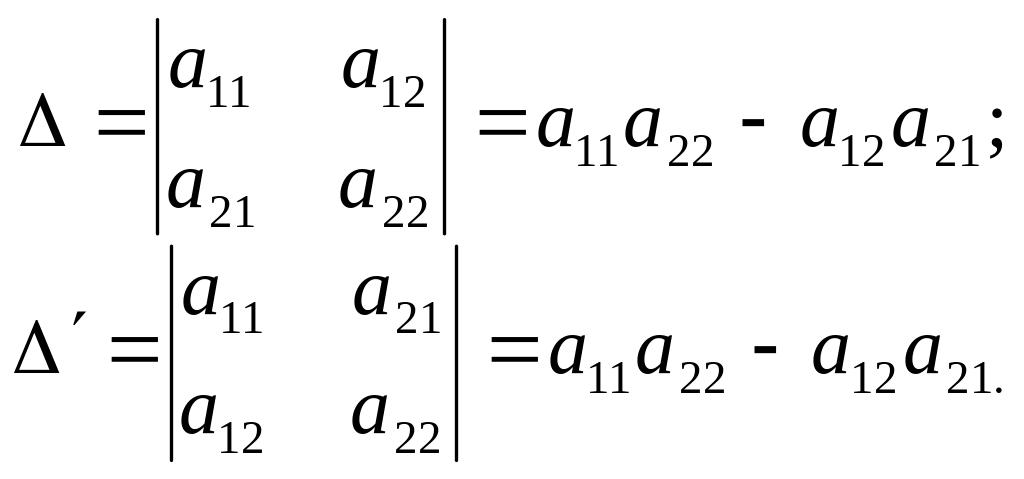
Отже,
![]() Аналогічно розглядаються
значення
Аналогічно розглядаються
значення
![]() .
.
2. Якщо переставити місцями два рядка (стовпці), то визначник змінить знак.
Доведення. Для маємо:
;
![]() .
.
Те ж саме матимемо для .
3. Якщо один з рядків (стовпців) визначника складається тільки з нулів, то визначник дорівнює нулю.
Це твердження видається очевидним, якщо визначник розкласти саме за цим рядком (стовпчиком).
4. Якщо визначник має два однакових рядки (стовпці), то він дорівнює нулю.
Доведення.
Переставимо
ці рядки місцями. Тоді
![]() ,
але
,
але
![]() (переставлені рядки однакові). Отже,
(переставлені рядки однакові). Отже,
![]() ,
звідки
,
звідки
![]() або
або
![]() .
.
5. Спільний множник, який міститься в усіх елементах одного рядка (стовпця), можна винести за знак визначника.
Доведення.
;
![]() .
□
.
□
6. Якщо у визначнику елементи двох рядків (стовпців) пропорційні, то визначник дорівнює нулю. Це забезпечують дві попередні властивості.
7. Якщо кожен елемент -го рядка ( -го стовпця) є сумою двох доданків, то такий визначник дорівнює сумі двох визначників, у одного з яких -й рядок ( -й стовпець) складається з перших доданків, а у другого – з других; інші елементи всіх трьох визначників однакові. Це можна довести розкладанням визначника за відповідним рядком або стовпчиком, розділивши далі суму на дві.
8. Визначник не зміниться, якщо до елементів одного рядка (стовпця) додати відповідні елементи іншого рядка (стовпця), помножені на одне й те саме число [18].
Доведення.
;
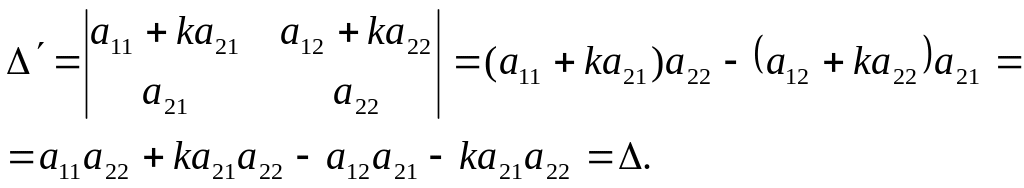
Для n>2 доведення можна провести на основі попередньої властивості.
Розглянемо основні методи обчислення визначників.
1.
Метод ефективного зниження порядку.
Використовуючи основні властивості
визначників, обчислення
![]() завжди можна звести до обчислення одного
визначника
-го
порядку, зробивши в будь-якому рядку
всі елементи, крім одного, рівними нулю.
Покажемо це на прикладі.
завжди можна звести до обчислення одного
визначника
-го
порядку, зробивши в будь-якому рядку
всі елементи, крім одного, рівними нулю.
Покажемо це на прикладі.
Приклад 2. Користуючись властивостями 1-9 визначника, обчислити визначник четвертого порядку
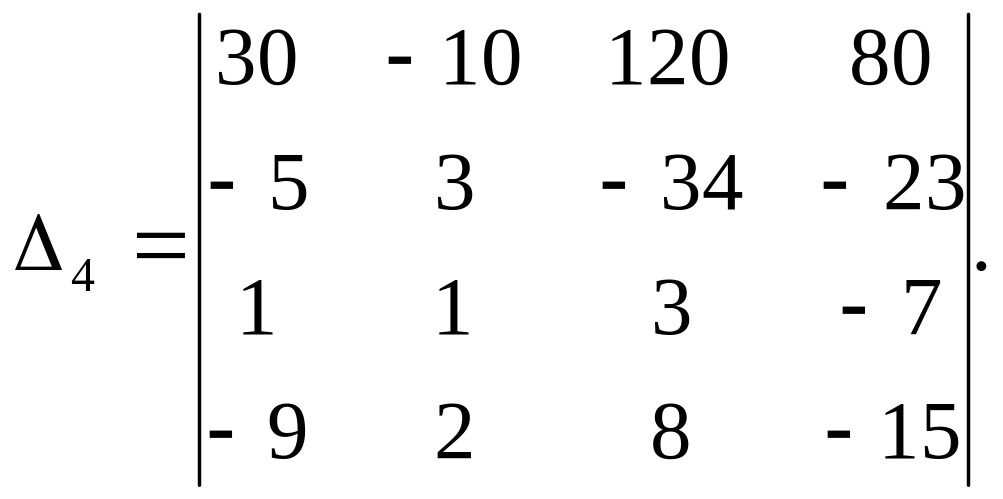
Розв’язання. За властивістю 5 визначників із першого рядка винесемо множник 10, а потім будемо послідовно множити отриманий рядок на 3, 1, 2 і додавати відповідно до другого, третього і четвертого рядків. Тоді, згідно з властивістю 8, маємо:

Отриманий визначник можна розкласти за елементами другого стовпця. Тоді
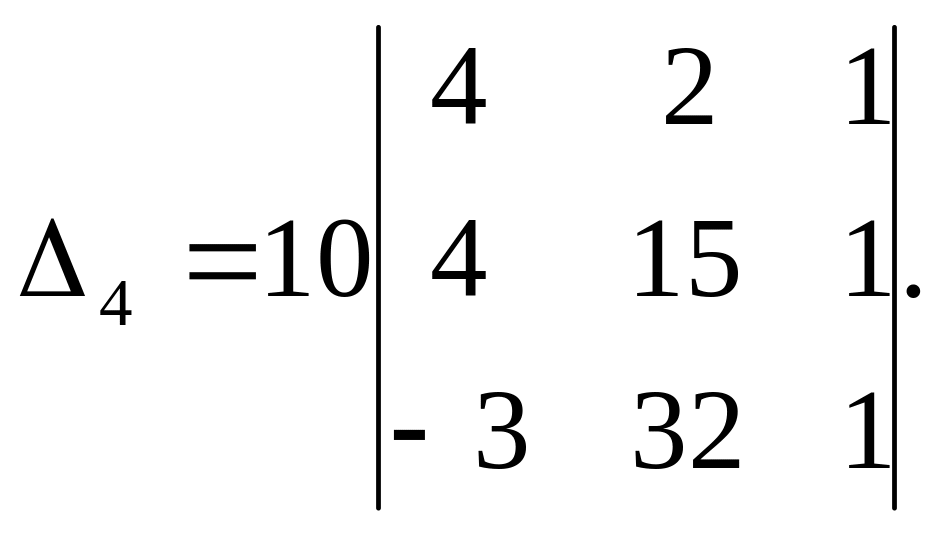
Отримали визначник третього порядку, який можна обчислити за правилом Саррюса або подібним прийомом звести до обчислення одного визначника другого порядку. Дійсно, віднявши із другого і третього рядків даного визначника перший рядок, отримаємо
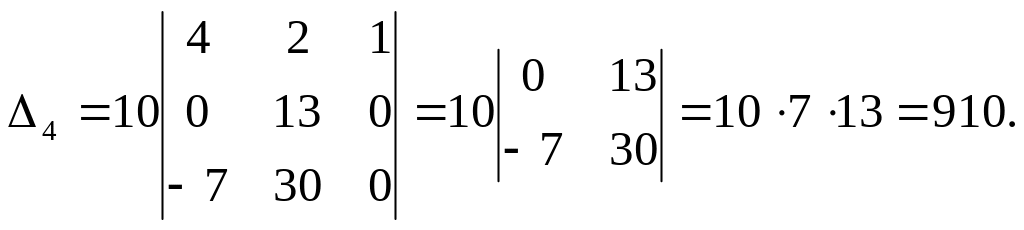
2.
Зведення визначника до трикутного
вигляду.
Визначник, у якого всі елементи, що
знаходяться вище або нижче головної
діагоналі, рівні нулю, називається
визначником трикутного виду. Очевидно,
що в цьому випадку визначник дорівнює
добутку елементів його головної
діагоналі. Зведення будь-якого визначника
![]() до трикутного виду завжди можливе.
до трикутного виду завжди можливе.
Приклад 3. Обчислити визначник
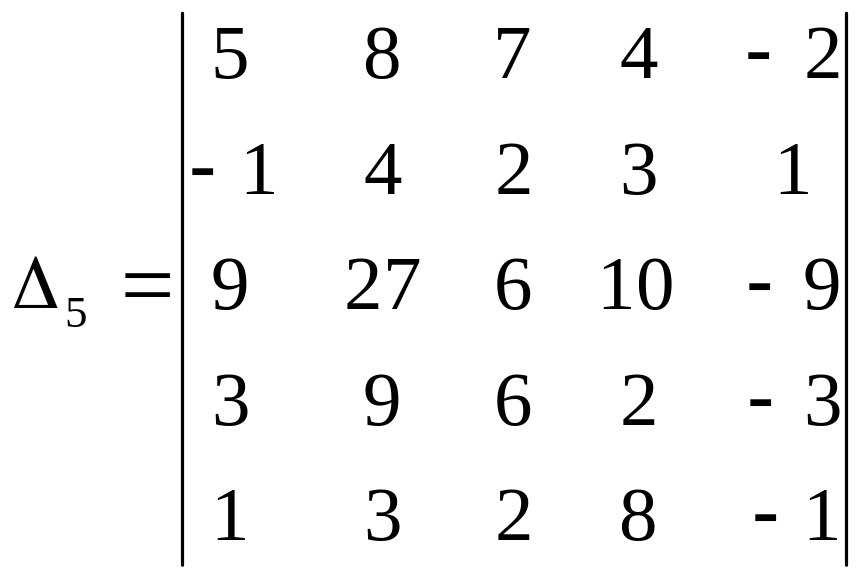 .
.
Розв’язання. Будемо робити нулі нижче головної діагоналі. Виконаємо наступні дії. П’ятий стовпчик визначника додамо до першого, цей же стовпчик, помножений на 3, - з другим, на 2 – з третім, на 8 – з четвертим стовпчиком. Таким чином в п’ятому рядку обнуляються всі елементи, крім останнього. Застосовуючи властивості визначників, отримаємо визначник трикутного виду, який дорівнює заданому:
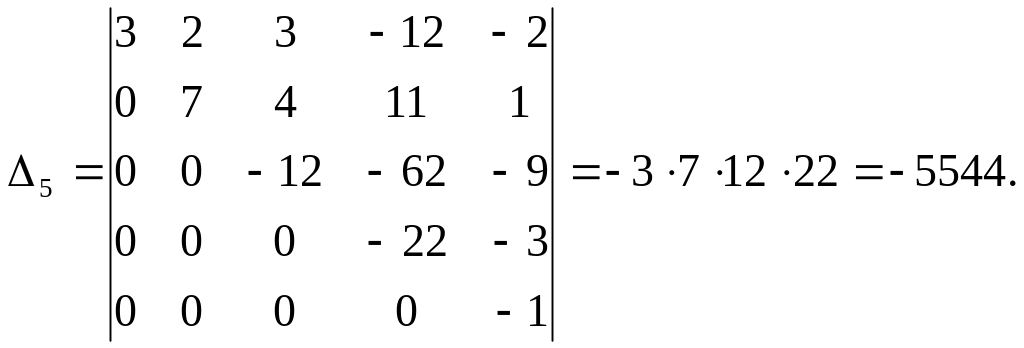
Зведення визначників до трикутного вигляду надалі буде використовуватися при розв’язанні систем лінійних рівнянь методом Жордана-Гаусса (його називають також методом Гаусса).
