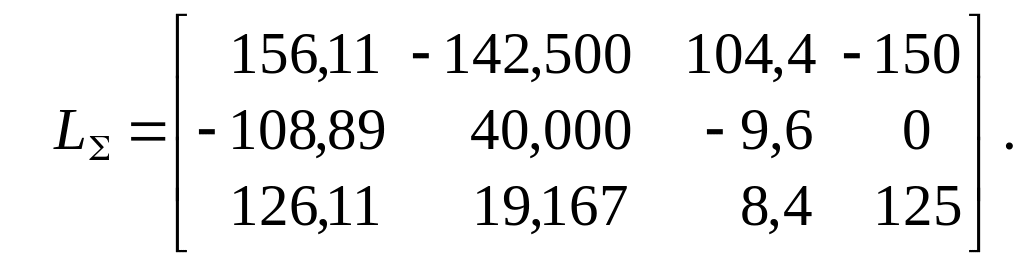- •3. Пример выполнения расчётного задания
- •3.1. Исходные данные
- •3.2. Степень статической неопределимости и выбор основной системы метода сил
- •3.3. Канонические уравнения метода сил. Определение и проверка коэффициентов и свободных членов
- •3.3.1. Единичные состояния основной системы. Определение и проверка коэффициентов кумс
- •3.3.2. Основная система при заданных силовых, температурных и кинематических воздействиях. Определение и проверка свободных членов уравнений
- •3.4. Компьютерный расчет рамы в матричной форме
- •3.4.1. Формирование матриц для расчёта по программе mefor
- •3.4.2. Исходные данные, вводимые в компьютер
- •3.4.3. Результаты расчета по программе mefor
- •3.4.4. Построение эпюр внутренних силовых факторов в рассчитываемой системе
- •3.4.5. Проверка результатов расчета рамы
- •3.4.6. Построение объемлющей эпюры изгибающих моментов
- •3.5. Вычисление перемещений в статически неопределимой раме
3.3.2. Основная система при заданных силовых, температурных и кинематических воздействиях. Определение и проверка свободных членов уравнений
 Для нахождения свободных членов
канонических уравнений рассматриваются
состояния основной системы, соответствующие
каждому из четырёх вариантов заданных
воздействий. Так как основная система
– статически определимая, то усилия в
ней возникают только от силовых
воздействий (
нагрузок
).
Для нахождения свободных членов
канонических уравнений рассматриваются
состояния основной системы, соответствующие
каждому из четырёх вариантов заданных
воздействий. Так как основная система
– статически определимая, то усилия в
ней возникают только от силовых
воздействий (
нагрузок
).
На рис. 3.8, а, в изображена основная система в двух «грузовых» состояниях – от нагрузок 1‑го ( f = 1 ) и 2‑го ( f = 2 ) вариантов заданных воздействий ( постоянной и первой временной нагрузок ). На рис. 3.8, б, г – соответствующие эпюры изгибающих моментов.
Перемещения в ОСМС по направлениям удаленных лишних связей от силовых воздействий двух первых вариантов ( f = 1, 2 ) определяем также методом Максвелла – Мора – по формуле, получаемой как частный случай ( 1.14 ) при учёте тех же видов деформаций элементов рамы, что и в выполненных выше вычислениях единичных перемещений:
i
=
1,
2,
3; f
= 1,
2.
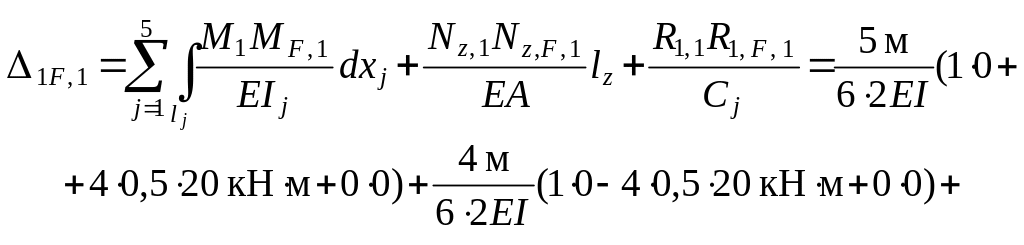
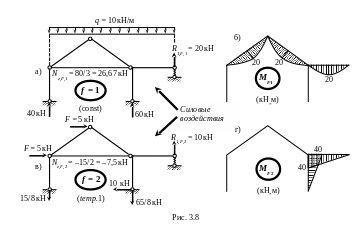
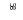
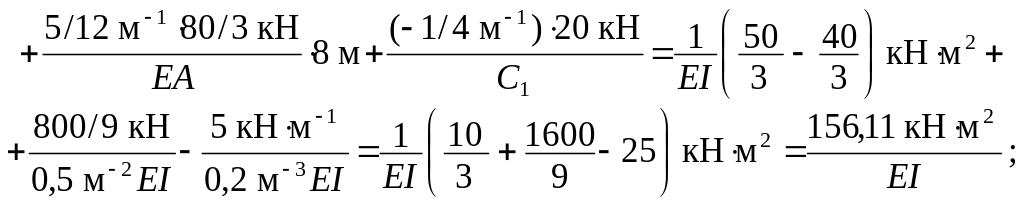
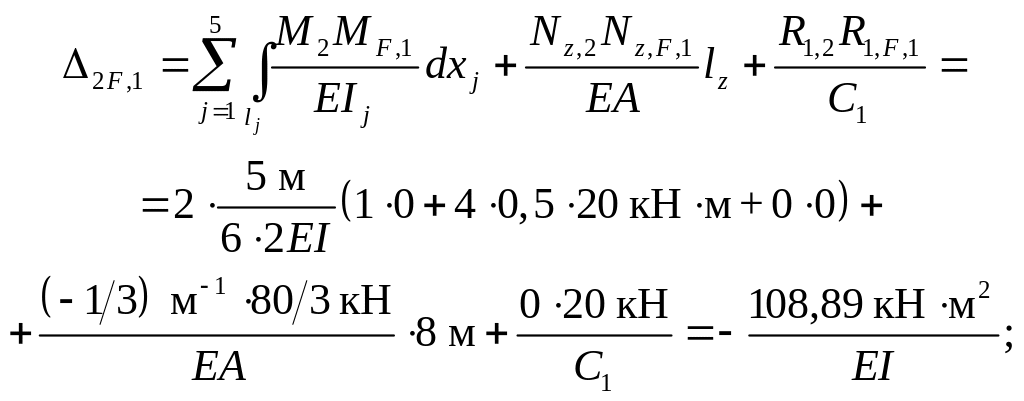
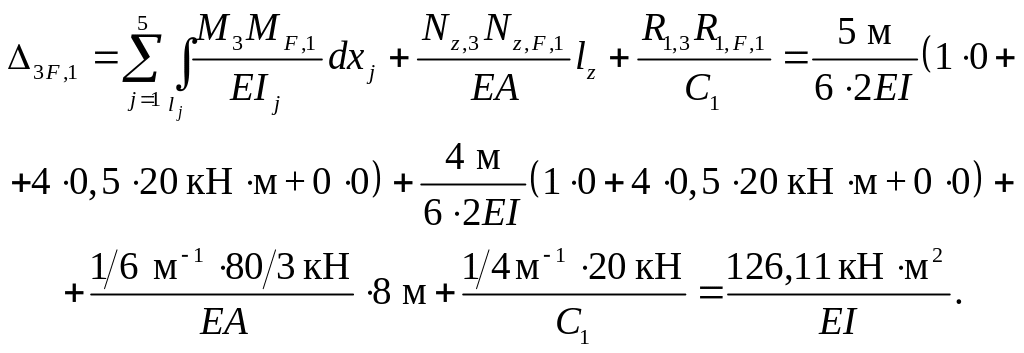
Перемещения iF, 1 ( i = 1, 2, 3 ) в ОСМС по направлениям ос-новных неизвестных Хi в случае постоянной нагрузки можно ис-
толковать по схеме деформаций, показанной на рис. 3.9:
q =
10 кН/м
F,
1
F,
1

F,
1
F,
1






 3F,
1 = F,
1 +
F,
1 .
3F,
1 = F,
1 +
F,
1 .
 Проверка правиль-
Проверка правиль-
н


 ости
вычисленных
«гру-
ости
вычисленных
«гру-
з
f
= 1 (const)
F,
1



 овых»
перемещений вы-
овых»
перемещений вы-
п
F,
1



 олняется
по условию
олняется
по условию
( 1.23 ), которое для рас-
с читываемой рамы в слу-
ч
Рис. 3.9
требует определения об-
общённого ( суммарного ) перемещения sF, 1 по формуле
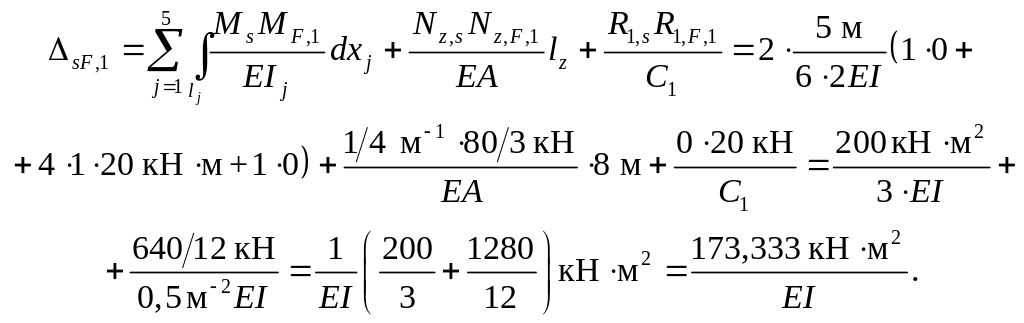
Сопоставляем полученный результат с суммой ранее найденных свободных членов канонических уравнений
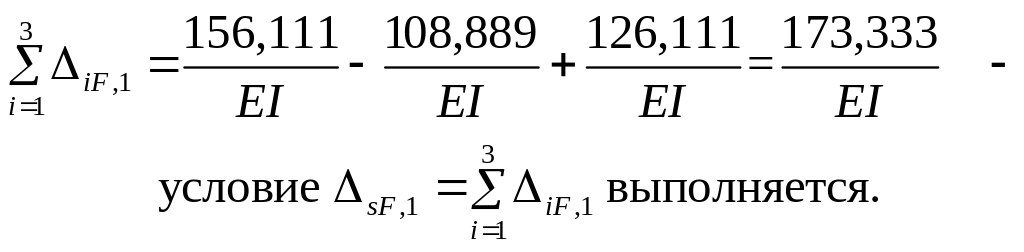
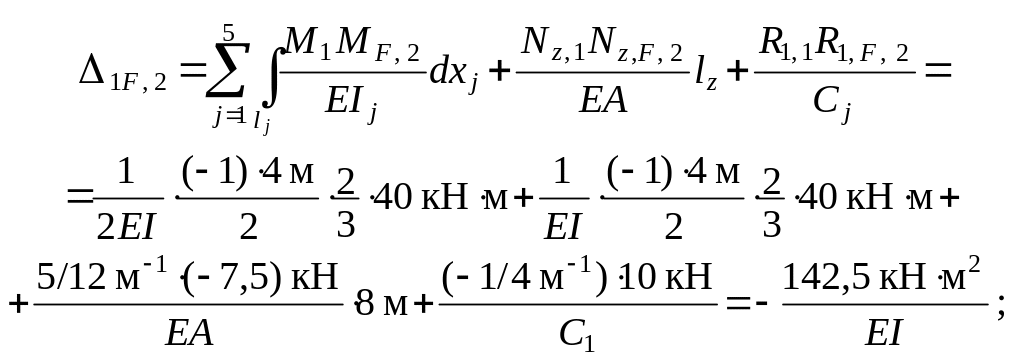
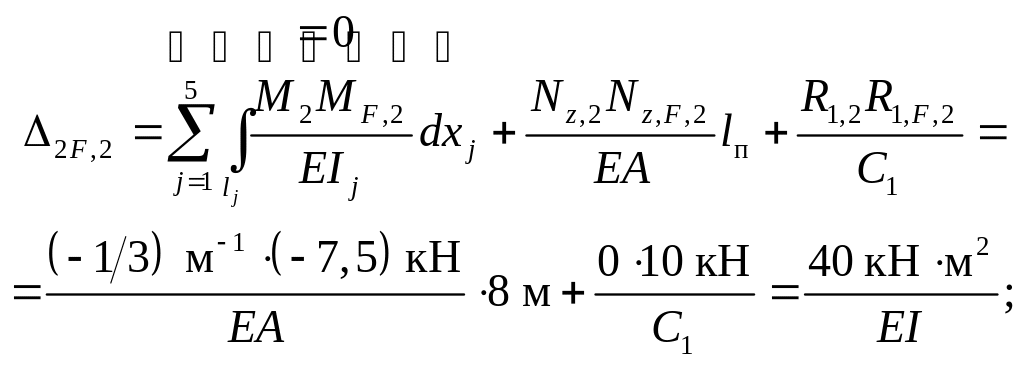

Проверка:
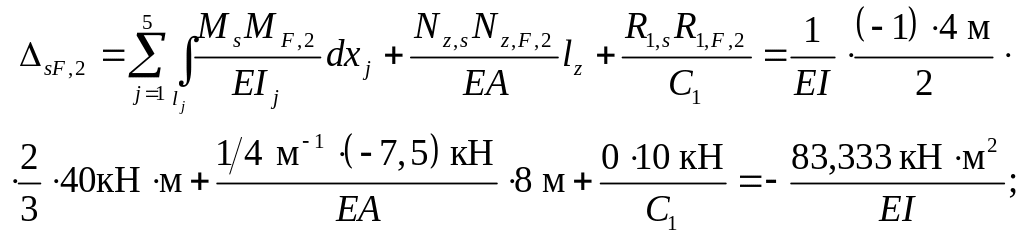

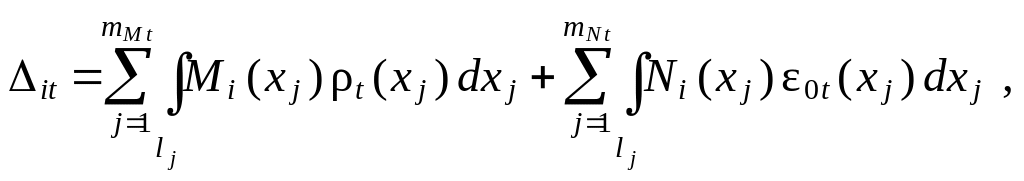
г
![]()
тогда
![]()
где
![]() –
площади эпюр Mi
и Ni
на j-ом
участке.
–
площади эпюр Mi
и Ni
на j-ом
участке.
На рис. 3.10 представлены расчётные данные о температурном режиме элементов рамы. Приращения температур t1 описываются на нижних волокнах горизонтальных стержней и на правых волокнах вертикальных элементов, а t2 – соответственно на верхних и левых. При вычислении составляющих приращений температуры элемента ( равномерной*) t0 и неравномерной tnr ) по формулам, воспроизведённым на рис. 3.10, обязательно учитываются знаки t1 и t2 .
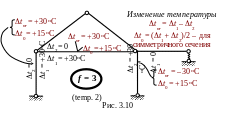
Кривизна оси левой стойки:
t,
l =![]() (0,3
м) =
(0,3
м) =
![]() м
–1 ;
м
–1 ;
д ля
правой стойки
t,
r
=
ля
правой стойки
t,
r
=
= – t, l = – м –1.
Кривизну оси затяж-
ки, не работающей на из-
гиб, можно не определять.
Относительные про-
дольные температурные
деформации стоек и за-
т
![]() .
.
=
*)
В случае
симметричного сечения t0
–
среднее
приращение температуры.
![]() =
=
Перемещения it ( i = 1, 2, 3 ) в ОСМС по направлениям основных неизвестных Хi в случае изменения температуры можно истолковать по схеме деформаций, показанной на рис. 3.11:
1t = t + t ; 2t = – t – t ; 3t = t + t .
Для удобства вычисления интегралов в выражении перемещений it строим эпюры t и 0t ( рис. 3.12 ), причём при построении эпюры t используем аналогию с эпюрой изгибающих моментов: знаки не проставляются, а ординаты откладываются со стороны более «тёплых» волокон элемента ( с алгебраически большим приращением температуры t1 или t2 ), т.е. со стороны выпуклости стержня, искривлённого тепловым воздействием. На эпюре 0t знаки указываются, подобно эпюре продольных сил.
Рис.3.12

Легко заметить, что в рассматриваемой задаче все температурные деформации прямо пропорциональны коэффициенту ЛТР материала , поэтому ординаты эпюр t и 0t можно было бы находить с точностью до общего множителя .
Выполняя «перемножение» единичных эпюр Mi и Ni соответственно с эпюрами t и 0t , находим температурные перемещения:
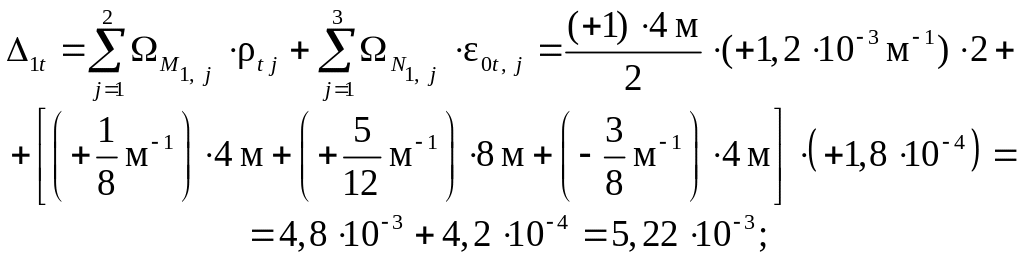
= 0
= 0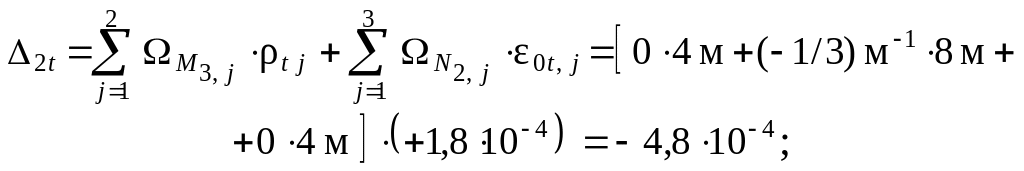


Универсальная проверка найденных перемещений ( свобод-ных членов канонических уравнений в случае температурного воздействия ) выполняется также с использованием суммарных единичных силовых факторов ( см. рис. 3.7 ) – моментов Ms и про-дольной силы в затяжке Nz, s = 1/4, при этом в левой и правой стойках Nl, s = Nr, s = 0:
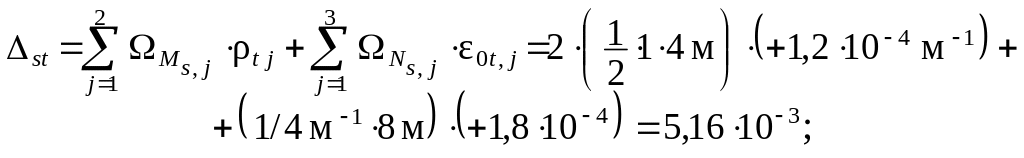
условие
![]()
![]() выполняется.
выполняется.
В последнем варианте воздействий ( f = 4 ) с заданными смещениями опор из расчётной схемы ОСМС ( рис. 3.12 ) берут- ся без каких-либо дополнительных вычислений только значения
компонентов смещений опорных связей. Нужно лишь следить за
1c
= –c
– c
2c
= c
– c
3c
= c
+ c
Рис. 3.12

тем, чтобы линейные перемещения были описаны в тех же единицах измерения, которые использовались для размеров рамы в расчёте реакций смещаемых связей в единичных состояниях ( см. рис. 3.4 ), т.е. в метрах.
Обратим внимание на то, что в статически определимой основной системе перемещения, вызванные смещениями опор, не сопровождаются деформациями элементов.
![]()
.
Значения реакций R(j), i по направлениям заданных смещений связей приведены на схемах единичных состояний ( рис. 3.4 ).
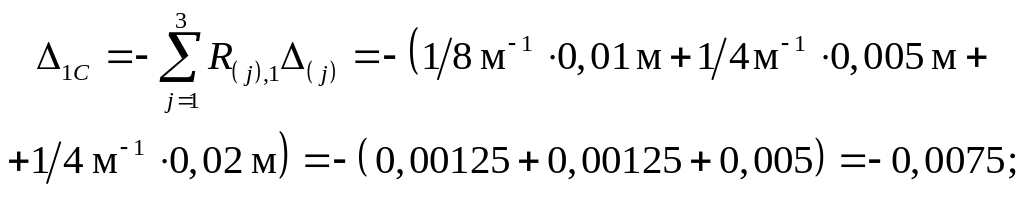
![]()
![]()
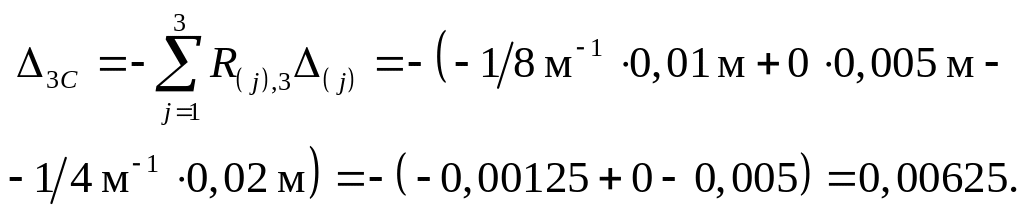
а)
б)
в)
г)
 Заметим,
что на напряжённо-деформированное
состояние рассматриваемой СНС с
шарнирными
опорами могут оказывать влияние только
линейные смещения опорных связей.
Повороты основания
Заметим,
что на напряжённо-деформированное
состояние рассматриваемой СНС с
шарнирными
опорами могут оказывать влияние только
линейные смещения опорных связей.
Повороты основания
(
 «земли»
)
не будут сказываться ни на
«земли»
)
не будут сказываться ни на
п
M1

 еремещениях,
ни
на
усилиях
в
раме
еремещениях,
ни
на
усилиях
в
раме
(
 рис.
3.13,
а
).
Но
при
наличии
опорных
рис.
3.13,
а
).
Но
при
наличии
опорных
з
c
c



![]()
в
R(4),
i
ся в расчёте. Например, если бы шар-
н
Рис. 3.13
положен выше опоры ( рис. 3.13, в ), то
угол поворота c следовало бы рассматривать как 4-й компонент (4) заданных смещений связей и соответственно в единичных состояниях ОСМС определять опорный момент R(4), i ( рис. 3.13, в ). При выбранных ранее основных неизвестных фрагмент эпюры изгибающих моментов от X1 = 1 имеет вид, показанный на рис.3.13, г, тогда R(4), 1 = = a/(h – a), где h – высота стойки. В остальных единичных состояниях R(4), 2 = R(4), 3 = 0. Найденную реакцию R(4), 1 нужно умножить на (4) и результат учесть при вычислении 1c.
Для проверки найденных ic используются суммарные реакции R(j), s ( вычисляемые, как и изгибающие моменты Ms , также независимо от ранее найденных R(j), i ) – см. рис. 3.7, из которого R(1), s = R(3), s = 0; R(2), s = 1/4.

условие
![]()
![]() выполняется.
выполняется.
Используя вычисленные и проверенные коэффициенты и свободные члены, формируем систему канонических уравнений, обращая внимание на то, что все единичные перемещения и перемещения от заданных силовых воздействий ( в первых двух вариантах, f = 1, 2 ) определены с точностью до множителя 1/(EI). Величина EI – общий параметр ( масштабная единица измерения жёсткостей, EI = C0 ), который при записи уравнений в матричной форме может быть вынесен из соответствующих матриц:
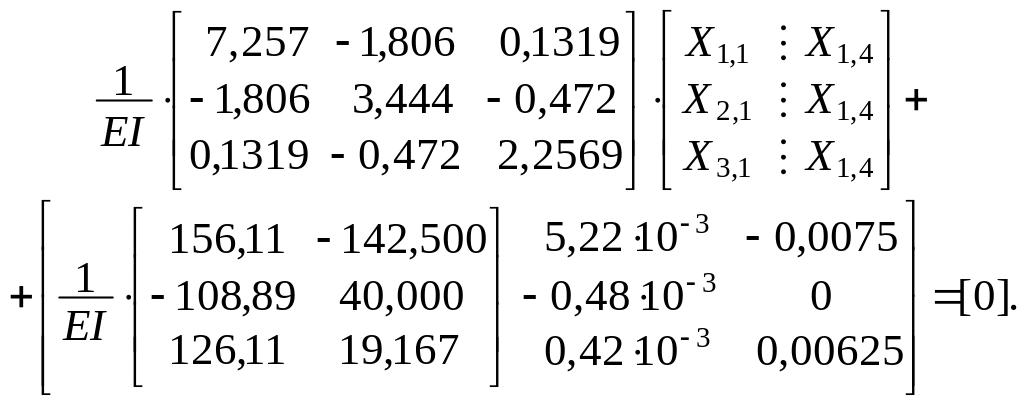
После умножения на EI получаем систему КУМС в виде

Очевидно,
что определение основных неизвестных
в первых двух вариантах воздействий
( силовых )
не требует знания числового значения
параметра EI, но для
вычисления реакций лишних связей и,
следовательно, всех искомых усилий в
рассчитываемой СНС от тепловых и
кинематических воздействий необходимо
использовать EI в
числовом выражении. Умножив компоненты
последних двух столбцов матрицы L
свободных членов на EI
=![]() (
см. п. 3.1
), получаем:
(
см. п. 3.1
), получаем: