3. Пример выполнения расчётного задания

3.1. Исходные данные

Требуется рассчитать методом сил раму, схема которой представлена на рис. 3.1. По результатам расчёта должны быть построены эпюры внутренних силовых факторов – изгибающих моментов, поперечных и продольных сил от четырёх вариантов воздействий: постоянной распределённой нагрузки q и трёх независимых друг от друга временных воздействий – двух сосредоточенных горизонтальных сил F, изменения температуры t на отмеченных штриховыми линиями сторонах стержней и от смещений опорных связей ₍₁₎ , ₍₂₎ , ₍₃₎ . На участке DK построить объемлющую эпюру M_расч и эпюры сил Q_Мрасч и N_Мрасч , соответствующих расчётным моментам. Определить угол поворота сечения 1 и горизонтальное перемещение узла K отдельно от по-стоянной нагрузки, изменения температуры и смещений связей.

Рис. 3.1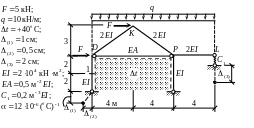

Высоты сечений стоек h_с = 0,3 м. Сечения стержней – симметричные относительно своих главных осей.

Примечание: в индивидуальном расчётном задании студента могут присутствовать параметры, которых нет в исходных данных рассматриваемого примера – относительно них необходимые объяснения приведены далее, например, об угловых упругих связях – на с. 54, по учёту угловых смещений опорных защемлений – на с. 65.

3.2. Степень статической неопределимости и выбор основной системы метода сил

Для выявления степени статической неопределимости рамы используем формулу ( 1.1 ), считая дисками стержень с лома-

ной осью, правый горизонтальный элемент и затяжку ( D = 3 ):

n_st = n_л.с. = – W = – 3D + 3П + 2H + C + C₀ = = 3 –

здесь учтена одна припайка в узле P ( П = 1), два простых шарнира в узлах D и P ( Н = 2 ), два опорных шарнира и внешняя линейная упругая связь ( С₀ = = 5 ).

По альтернативной формуле ( 1.2 ): n_st = 3K – Н = = 3

( все шарниры – простые, соединяющие диски попарно ).

X₂

Для выбора основной системы метода сил рассматриваем несколько предварительно намеченных вариантов – они изобра-жены на рис. 3.2, где заданные воздействия условно не показаны.

Рис. 3.2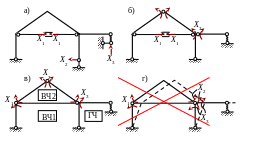

Сравнение вариантов: вариант «г» отвергается ввиду геометрической изменяемости системы  ; ОСМС по варианту «а» хуже других ( см. рекомендацию 2 на с. 9 ), так как получена удалением линейных связей, в том числе опорных. Выполнив кинематический анализ остальных систем, убеждаемся в их геоме-трической неизменяемости. Рациональным является вариант «в» основной системы, поскольку в нём, во-первых, осуществлено удаление только угловых связей, а во-вторых, имеются главная часть ( ГЧ ) и две второстепенных ( ВЧ 1 и ВЧ 2 ) – все с достаточно простой структурой  ( см. рекомендации 3 и 4 ).

Выбранная для расчёта основная система представлена на рис. 3.3. Она статически определима ( = 3K – Н = = 0

– учтено, что шарниры в узлах D и Р кратные – двойные ).

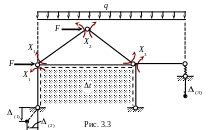
На схеме даны одновременно все варианты заданных воздействий; в дальнейшем они будут рассматриваться раздельно.