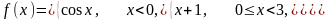Задание № 5
Задана функция y = f (x). Установить, является ли данная функция непрерывной. В случае разрыва функции в некоторой точке найти ее пределы слева и справа, классифицировать характер разрыва. Построить схематично график функции.
5.1 |
|
5.16 |
|
5.2 |
|
5.17 |
|
5.3 |
|
5.18 |
|
5.4 |
|
5.19 |
|
5.5 |
|
5.20 |
|
5.6 |
|
5.21 |
|
5.7 |
|
5.22 |
|
5.8 |
|
5.23 |
|
5.9 |
|
5.24 |
|
5.10 |
|
5.25 |
|
5.11 |
|
5.26 |
|
5.12 |
|
5.27 |
|
5.13 |
|
5.28 |
|
5.14 |
|
5.29 |
|
5.15 |
|
5.30 |
|
Задание № 6
Дано уравнение f (x) = 0. Требуется: 1) графическим методом отделить корень этого уравнения; 2) найти этот корень с точностью до 0,1 методом деления отрезка пополам.
6.1. |
2x + 5x = 0. |
6.2. |
х3 + 2х – 7 = 0 |
6.3. |
х – (х + 1)3 = 0. |
6.4. |
ln x + 5x = 0. |
6.5. |
x ln x – 4 = 0. |
6.6. |
х3 + 3х – 7 = 0. |
6.7. |
ln x – 6 + 7x = 0. |
6.8. |
3x + 4x = 0. |
6.9. |
4x + 2x = 0. |
6.10. |
5x + 3x = 0. |
6.11. |
2x + 2x – 2 = 0. |
6.12. |
ln x + 3x – 2 = 0. |
6.13. |
2х + 5х – 3 = 0. |
6.14. |
ln x + 3x – 1 = 0. |
6.15. |
x ln x – 5 = 0. |
6.16. |
2ex – x2 = 0. |
6.17. |
ln x – 5 + 6x = 0. |
6.18. |
4x + 5x = 0. |
6.19. |
ex + 3x = 0. |
6.20. |
4x + 3x = 0. |
6.21. |
ex + 5x = 0. |
6.22. |
3x2 – 7ex = 0. |
6.23. |
3x + x = 0. |
6.24. |
2 ln x + 5x = 0. |
6.25. |
3x ln x – 7 = 0. |
6.26. |
х3 + 4х + 1 = 0. |
6.27. |
ln x – 7 + 8x = 0. |
6.28. |
23x + 7x = 0. |
6.29. |
34x + 7x = 0. |
6.30. |
25x + 7x = 0. |