
Задание № 3
Даны уравнения линии r = r () в полярной системе координат. Требуется:
1) построить линию по точкам на промежутке от = 0 до = 2 с шагом, равным ;
2) найти уравнение линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью;
3) назвать линию, найти координаты центра и полуоси.
3.1.
|
3.2.
|
3.3.
|
3.4.
|
3.5.
|
3.6.
|
3.7.
|
3.8.
|
3.9.
|
3.10.
|
3.11.
|
3.12.
|
3.13.
|
3.14.
|
3.15.
|
3.16.
|
3.17.
|
3.18.
|
3.19.
|
3.20. . |
3.21.
|
3.22.
|
3.23.
|
3.24.
|
3.25.
|
3.26.
|
3.27.
|
3.28.
|
3.29.
|
3.30.
|
Задание № 4
Найти пределы функций.
4.1.
а)
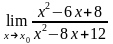 при
при
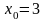 ,
,
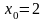 ,
,
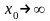 ;
;
б)
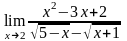 ;
в)
;
в)
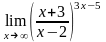 ;
г)
;
г)
 .
.
4.2.
а)
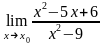 при
при
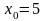 ,
,
;
,
,
;
б)
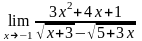 ;
в)
;
в)
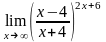 ;
г)
;
г)
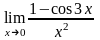 .
.
4.3.
а)
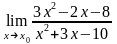 при
при
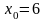 ,
,
;
,
,
;
б)
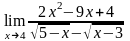 ;
в)
;
в)
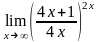 ;
г)
;
г)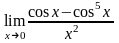 .
.
4.4.
а)
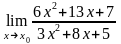 при
при
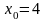 ,
,
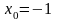 ,
;
,
;
б)
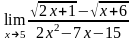 ;
в)
;
в)
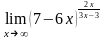 ;
г)
;
г)
 .
.
4.5.
а)
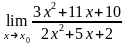 при
при
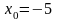 ,
,
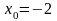 ,
;
,
;
б)
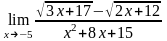 ;
в)
;
в)
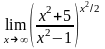 ;
г)
;
г)
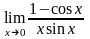
4.6.
а)
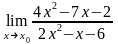 при
при
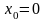 ,
,
;
,
,
;
б)
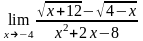 ;
в)
;
в)
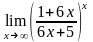 ;
г)
;
г)
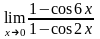 .
.
4.7.
а)
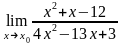 при
при
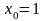 ,
,
;
,
,
;
б)
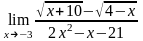 ;
в)
;
в)
 ;
г)
;
г)
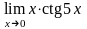 .
.
4.8.
а)
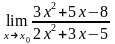 при
,
,
;
при
,
,
;
б)
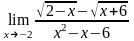 ;
в)
;
в)
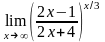 ;
г)
;
г)
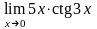 .
.
4.9.
а)
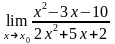 при
,
,
;
при
,
,
;
б)
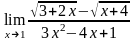 ;
в)
;
в)
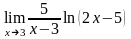 ;
г)
;
г)
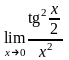 .
.
4.10.
а)
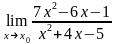 при
,
,
;
при
,
,
;
б)
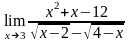 ;
в)
;
в)
 ;
г)
;
г)
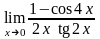 .
.
4.11 а)
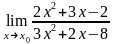 при
при
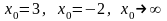 ;
;
б)
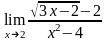 ;
в)
;
в)
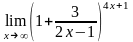 ;
г)
;
г)
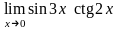 .
.
4.12 а)
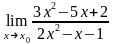 при
при
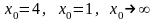 ;
;
б)
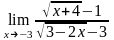 ;
в)
;
в)
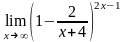 ;
г)
;
г)
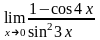 .
.
4.13 а)
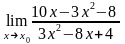 при
при
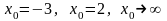 ;
;
б)
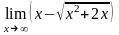 ;
в)
;
в)
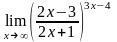 ;
г)
;
г)
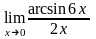 .
.
4.14 а)
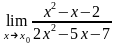 при
при
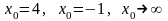 ;
;
б)
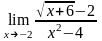 ;
в)
;
в)
 ;
г)
;
г)
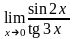 .
.
4.15 а)
 при
при
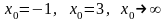 ;
;
б)
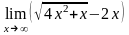 ;
в)
;
в)
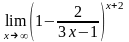 ;
г)
;
г)
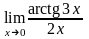 .
.
4.16 а)
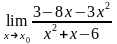 при
при
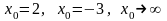 ;
;
б)
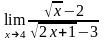 ;
в)
;
в)
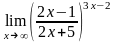 ;
г)
;
г)
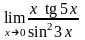 .
.
4.17 а)
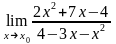 при
при
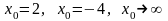 ;
;
б)
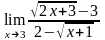 ;
в)
;
в)
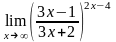 ;
г)
;
г)
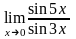 .
.
4.18 а)
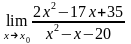 при
при
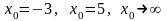 ;
;
б)
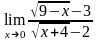 ;
в)
;
в)
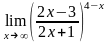 ;
г)
;
г)
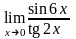 .
.
4.19 а)
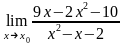 при
при
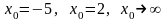 ;
;
б)
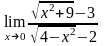 ;
в)
;
в)
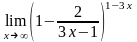 ;
г)
;
г)
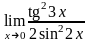 .
.
4.20 а)
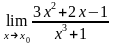 при
при
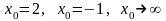 ;
;
б)
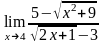 ;
в)
;
в)
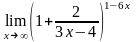 ;
г)
;
г)
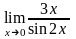 .
.
4.21 а)
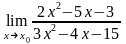 при
при
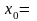 2,
3,
;
2,
3,
;
б)
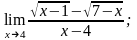 в)
в)
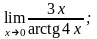
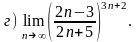
4.22 а) при 0, 2, ;
б)
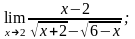 в)
в)
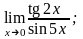
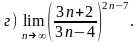
4.23 а)
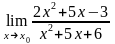 при
3,
–3,
;
при
3,
–3,
;
б)
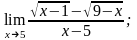 в)
в)
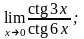
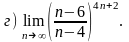
4.24 а)
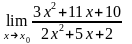 при
–3,
–2,
;
при
–3,
–2,
;
б)
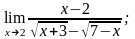 в)
в)

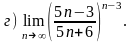
4.25 а)
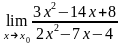 при
2,
4,
;
при
2,
4,
;
б)
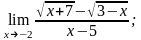 в)
в)
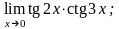
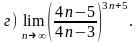
4.26 а)
 при
2,
5,
;
при
2,
5,
;
б)
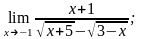 в)
в)
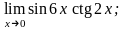
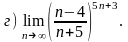
4.27 а)
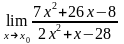 при
1,
–4,
;
при
1,
–4,
;
б)
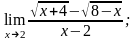 в)
в)
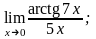
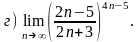
4.28 а)
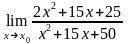 при
5,
–5,
;
при
5,
–5,
;
б)
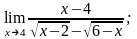 в)
в)
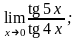
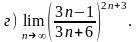
4.29 а) при –2, 1, ;
б)
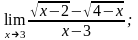 в)
в)
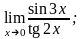
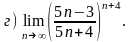
4.30 а) при –2, –1, ;
б)
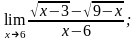 в)
в)
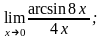
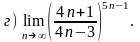

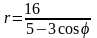 .
.
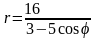 .
.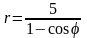 .
.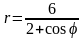 .
.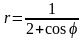 .
.
 .
.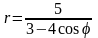 .
.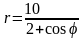 .
.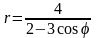 .
.
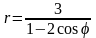 .
.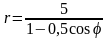 .
. .
.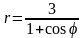 .
.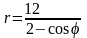 .
.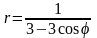 .
.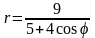 .
.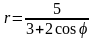 .
.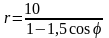 .
.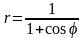 .
.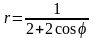 .
.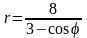 .
. .
.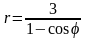 .
.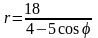 .
.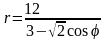
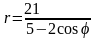 .
.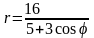
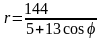 .
. .
.