
- •Перед решением злп ее необходимо привести к канонической форме записи. При этом используются следующие основные приемы:
- •При условиях:
- •2. Симплексный метод решения задач линейного программирования
- •Оптимальное решение определяется следующим образом: базисные переменные приравниваются соответствующим правым частям, остальные нулю.
- •2.4.Двойственность в линейном программировании
- •В теории двойственности важное значение имеют две теоремы, определяющие связь между решениями прямой и двойственной задач.
- •Транспортная задача линейного программирования имеет следующие особенности:
- •Алгоритм метода потенциалов:
- •Задача о назначениях.
- •Задача коммивояжера
- •Задача о покрытии
- •Задача о разбиении. Задача о разбиении аналогична задачи о покрытии с тем отличием, что признаки у различных предметов не должны совпадать:
- •Задача о взвешенном разбиении формулируется следующим образом:
- •Принятие решений
- •Пример реализации поиска решения в ms Excel
Алгоритм метода потенциалов:
1). Построение первоначального опорного плана.
2).
Определение потенциалов пунктов
отправления (ui)
и пунктов назначения (![]() ).
).
Потенциалы
находят из системы уравнений![]() где Cij
- тарифы, стоящие в заполняемых клетках
таблицы. Число переменных в этой системе
равно m+n, число уравнений m+n-1. Для
нахождения решения системы один из
потенциалов приравнивается произвольному
числу (например, u1=0)
и последовательно находятся значения
всех остальных потенциалов.
где Cij
- тарифы, стоящие в заполняемых клетках
таблицы. Число переменных в этой системе
равно m+n, число уравнений m+n-1. Для
нахождения решения системы один из
потенциалов приравнивается произвольному
числу (например, u1=0)
и последовательно находятся значения
всех остальных потенциалов.
3). Проверка оптимальности плана.
Проверяем
условия оптимальности:
![]() для всех свободных клеток. Вычисляем
для всех свободных клеток. Вычисляем
![]() - оценки свободных переменных для
оптимального базиса. Если все
- оценки свободных переменных для
оптимального базиса. Если все
![]() ,
то получаемый план является оптимальным,
иначе - к шагу 4.
,
то получаемый план является оптимальным,
иначе - к шагу 4.
4). Выбор переменной для включения в базис (выбор клетки, в которую необходимо послать переменную).
![]() .
Если таких клеток несколько, то для
заполнения выбирается клетка, имеющая
минимальный тариф.
.
Если таких клеток несколько, то для
заполнения выбирается клетка, имеющая
минимальный тариф.
5). Построение цикла пересчета для выбранной свободной клетки i0j0.
Циклом в таблице условий ТЗ называется ломаная линия, которая начинается в свободной клетке, и вершины которой (кроме начальной) расположены в занятых клетках, а звенья параллельны строкам и столбцам. При правильном построении опорного плана для каждой свободной клетки таблицы можно построить только один цикл.
После построения цикла его вершины последовательно отмечаются знаками «+» и «-», причем свободной клетке приписывается знак «+».
6). Определение величины перераспределения груза.
![]() ,
где xij
- перевозки, стоящие в вершинах цикла,
отмеченных знаком «-». Клетку, которой
соответствует d, обозначим через i1j1.
,
где xij
- перевозки, стоящие в вершинах цикла,
отмеченных знаком «-». Клетку, которой
соответствует d, обозначим через i1j1.
7). Сдвиг по циклу пересчета (перераспределение грузов).
В выбранную для заполнения свободную клетку (i0,j0) заносится значение d. Одновременно это число прибавляется к значениям перевозок, стоящих в клетках со знаком «+», и вычитается из значений перевозок, стоящих в клетках со знаком «-». Т.о. клетка (i0,j0) становится занятой, а i1j1 - свободной.
Замечание: при сдвиге по циклу пересчета число занятых клеток остается const=n+m-1. Если d соответствует нескольким клеткам таблицы, то освобождают одну из них, а в остальные записываются нулевые перевозки и считают их занятыми. Нулевые перевозки записываются и в клетки, которые имеют меньшие тарифы.
8). Переход к шагу 2.
Пример. На 3-х складах сосредоточен однородный груз в количествах 80, 100, и 70 единиц. Данный груз необходимо доставить 4-м потребителям, потребности которых равны соответственно 80, 50, 50, 70 единиц. Матрица тарифов имеет вид:
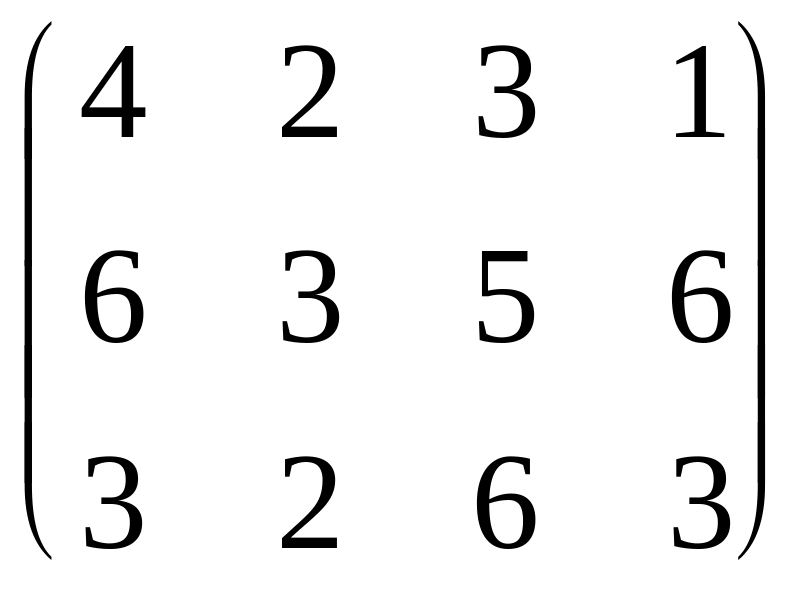 .
Необходимо определить: оптимальный
план перевозок.
.
Необходимо определить: оптимальный
план перевозок.
Составим таблицу транспортной задачи. Начальный план перевозок определим методом минимального элемента. При этом сначала помещаем 70 единиц груза в клетку с индексом 14, имеющую минимальный тариф, затем 10 единиц в клетку 12, 40 единиц в клетку 32, 30 единиц в клетку 38, 50 единиц в клетку 23, 50 единиц в клетку с индексом 21.
Пункты отправления |
Пункты назначения |
Запасы |
|||
B1 |
B2 |
B3 |
B4 |
||
A1 |
4 |
2 |
3 |
1 |
80 |
|
10 |
|
70 |
||
A2 |
6 |
3 |
5 |
6 |
100 |
50 |
|
50 |
|
||
A3 |
3 |
2 |
6 |
3 |
70 |
30 |
40 |
|
|
||
Потребности |
80 |
50 |
50 |
70 |
|
Затем определяем потенциалы пунктов отправления и потенциалы пунктов назначения. Для этого составляем уравнения для занятых клеток таблицы:
U1 +V2 = 2
U1 +V4 = 1
U2 +V1 = 6
U2 +V3 = 5
U3 +V1 = 3
U3 +V2 = 2
положим U1 = 0 и последовательно найдем значения остальных потенциалов.
Получим: U1 = 0, U2 = 3, U3 = 0, V1 = 3, V2 = 2, V3 = 2, V4 = 1.
Вычислим оценки ij для всех свободных клеток таблицы:
11 = 0 + 3 – 4 = -1
13 = 0 + 2 – 3 = -1
22 = 3 + 2 – 3 = 2
24 = 3 + 1 – 6 = -2
33 = 0 + 2 – 6 = -4
34 = 0 + 1 – 3 = -2
Выбираем максимальную положительную оценку. Это оценка 22 = 2. Следовательно, на следующем шаге будет заполнятся клетка с индексом 22. Составим цикл пересчета для данной клетки и пометим его вершины последовательно знаками «+» и «–»:
Пункты отправления |
Пункты назначения |
Запасы |
|||
B1 |
B2 |
B3 |
B4 |
||
A1 |
4 |
2 |
3 |
1 |
80 |
|
10 |
|
70 |
||
|
|
|
|
|
|
3 |
5 |
6 |
100 |
||
|
50 |
|
50 |
|
|
3 |
2 |
6 |
3 |
||
|
30 |
40 |
|
|
|
Потребности80505070
Определим величину перераспределения груза как минимальную из величин, стоящих в минусовых клетках. Это 40 единиц. Прибавляем данную величину к величинам перевозок, стоящим в клетках со знаком + и вычитаем ее из величин перевозок, стоящих в клетках со знаком – :
Пункты отправления |
Пункты назначения |
Запасы |
|||
B1 |
B2 |
B3 |
B4 |
||
A1 |
4 |
2 |
3 |
1 |
80 |
|
|
|
70 |
||
A2 |
6 |
3 |
5 |
6 |
100 |
10 |
40 |
50 |
|
||
A3 |
3 |
2 |
6 |
3 |
70 |
70 |
|
|
|
||
Потребности |
80 |
50 |
50 |
70 |
|
Составляем систему уравнений для определения потенциалов и последовательно находим из нее значения всех потенциалов.
U1 +V2 = 2
U1 +V4 = 1
U2 +V1 = 6
U2 +V2 = 3
U2 +V3 = 5
U3 +V1 = 3
Тогда,
U1 = 0, U2 = 1, U3 = -2, V1 = 5, V2 = 2, V3 = 4, V4 = 1.
Пересчитываем оценки:
11 = 0 + 5 – 4 = 1
13 = 0 – 2 + 3 = 1
24 = 1 + 1 – 6 = - 4
32 = -2 + 2 – 2 = -2
33 = -2 + 4 – 6 = -4
34 = -2 + 1 – 3 = -4
Имеем две максимальные положительные оценки 11 = 13 = 1. Для заполнения на следующем шаге целесообразно выбрать клетку с индексом 13, т.к. ей соответствует меньший тариф. Строим цикл пересчета для клетки 13:
Пункты отправления |
Пункты назначения |
Запасы |
|||
B1 |
B2 |
B3 |
B4 |
||
A1 |
|
|
|
|
|
2 |
3 |
1 |
80 |
||
|
|
10 |
|
70 |
|
6 |
3 |
5 |
6 |
||
|
10 |
40 |
50 |
|
|
3 |
2 |
6 |
3 |
||
|
70 |
|
|
|
|
80505070
Величина перераспределения груза равна 10. Перераспределяем груз:
Пункты отправления |
Пункты назначения |
Запасы |
|||
B1 |
B2 |
B3 |
B4 |
||
A1 |
4 |
2 |
3 |
1 |
80 |
|
|
10 |
70 |
||
A2 |
6 |
3 |
5 |
6 |
100 |
10 |
50 |
40 |
|
||
A3 |
3 |
2 |
6 |
3 |
70 |
70 |
|
|
|
||
|
80 |
50 |
50 |
70 |
|
Находим потенциалы пунктов отправления и назначения:
U1 +V3 = 3
U1 +V4 = 1
U2 +V1 = 6
U2 +V2 = 3
U2 +V3 = 5
U3 +V1 = 3
U1 = 0, U2 = 2, U3 = -1, V1 = 4, V2 = 1, V3 = 3, V4 = 1.
Пересчитываем оценки:
11 = 0 + 4 – 4 = 0
12 = 0 + 1 – 2 = -1
24 = 2 + 1 – 6 = -3
32 = -1 + 1 – 2 = -2
33 = -1 + 3 – 6 = -4
34 = -1 + 1 – 3 = -3
Все оценки неотрицательны. Следовательно, полученный план перевозок является оптимальным.
ЦЕЛОЧИСЛЕННОЕ ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Задачей целочисленного линейного программирования (ЗЦЛП) называется задача линейного программирования, в которой на переменные наложено требование целочисленности. При этом если все переменные задачи должны принимать целочисленные значения, задача называется полностью целочисленной, иначе – частично целочисленной. Если множество допустимых решений задачи является конечным, то задача называется комбинаторной. В-частности, к классу комбинаторных относятся задачи булевой оптимизации, в которых переменные могут принимать только два значения: 0 или 1.
Прикладные задачи целочисленного программирования
Задача о раскрое.
Для
изготовления заготовок D1,…,Dm
имеется n способов раскроя материала
A1,…,An.
![]() -количество заготовок i-го типа, получаемых
из единицы материала при способе Aj.
Имеется D единиц материала. При раскрое
единицы материала по способу Aj
имеются отходы площадью
-количество заготовок i-го типа, получаемых
из единицы материала при способе Aj.
Имеется D единиц материала. При раскрое
единицы материала по способу Aj
имеются отходы площадью
![]() .
Надо произвести не менее
.
Надо произвести не менее
![]() заготовок i-го типа и выполнить план с
минимизацией отходов.
заготовок i-го типа и выполнить план с
минимизацией отходов.
Таблица 11
Виды заготовок |
Способы раскроя |
План производства |
|||
A1 |
A2 |
… |
An |
||
D1 D2 … Dm |
A11 a21 ... am1 |
a12 a22 ... am2 |
... ... ... ... |
a1n a2 n ... amn |
b1 b2 ... bm |
Отходы |
C1 |
c2 |
… |
cn |
|
Пусть![]() - количество единиц материала,
раскраиваемого по j-му способу.
- количество единиц материала,
раскраиваемого по j-му способу.
Математическая модель задачи запишется следующим образом:

![]() ;
;
![]() .
.
Задача
о ранце.
Имеются предметы n видов, для каждого
предмета j-го вида (j=1,n) известны его
объем
![]() и стоимость
и стоимость
![]() .
Необходимо определить такой набор
предметов, суммарный объем которых не
превышал бы заданного числа b, а суммарная
ценность была бы максимальной. Эта
задача интерпретируется как задача
загрузки ранца объема b и называется
одномерной
задачей о ранце.
.
Необходимо определить такой набор
предметов, суммарный объем которых не
превышал бы заданного числа b, а суммарная
ценность была бы максимальной. Эта
задача интерпретируется как задача
загрузки ранца объема b и называется
одномерной
задачей о ранце.
Введем
целочисленные переменные
![]() ,
значения которых характеризует количество
предметов j-го вида, помещенных в ранец.
Тогда математическая модель данной
задачи имеет вид:
,
значения которых характеризует количество
предметов j-го вида, помещенных в ранец.
Тогда математическая модель данной
задачи имеет вид:
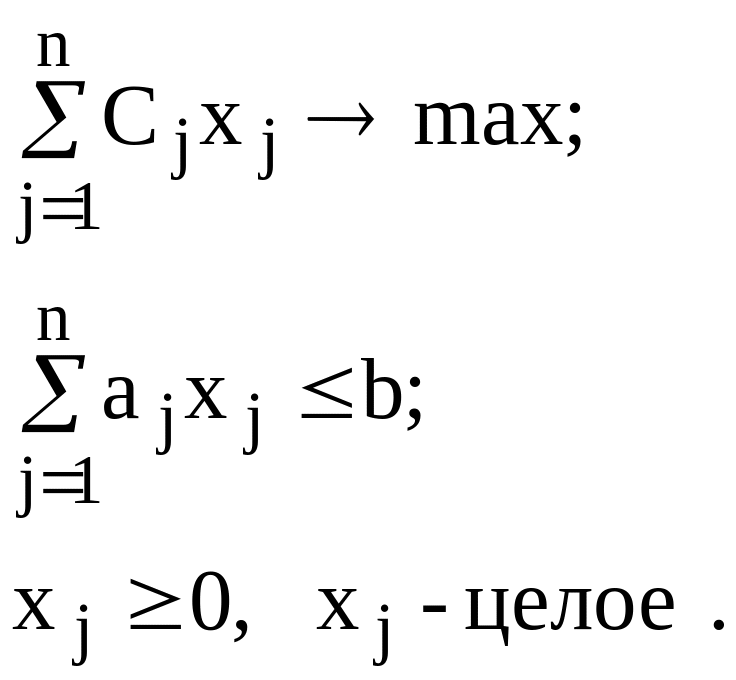
Если
ограничениями могут быть не только
объем ранца, но и другие его характеристики
![]() ,
то получим многомерную
задачу о ранце.
,
то получим многомерную
задачу о ранце.

В
случае, если количество предметов j-го
вида ограничено и равно
![]() ,
к задаче добавляется ограничение
,
к задаче добавляется ограничение
![]() .
Если
.
Если
![]() =1,
то получим задачу
о ранце с булевыми переменными.
Тогда
=1,
то получим задачу
о ранце с булевыми переменными.
Тогда
![]() ,
причем
,
причем
![]() ,
если j-й предмет помещен в ранец,
,
если j-й предмет помещен в ранец,
![]() в противном случае.
в противном случае.
К задаче о ранце сводится широкий класс задач дискретной оптимизации с ограниченными ресурсами.
Пример
8. Для оценки
работоспособности систем перед их
эксплуатацией производится проверка
их функционирования. При проверке
контролируются отдельные параметры
системы, каждый из которых характеризуется
вероятностью отказа проверяемых
элементов
![]() и временем контроля
и временем контроля
![]() .
Так как допустимое время контроля всей
системы T
ограничено, то для проверки необходимо
выбрать параметры, контролирующие
наиболее ненадежные элементы и требующие
для контроля наименьшего времени.
.
Так как допустимое время контроля всей
системы T
ограничено, то для проверки необходимо
выбрать параметры, контролирующие
наиболее ненадежные элементы и требующие
для контроля наименьшего времени.
Пусть n – общее количество параметров. Введем альтернативные булевы переменные:
![]()
Тогда математическую модель задачи можно сформулировать как одномерную задачу о ранце:
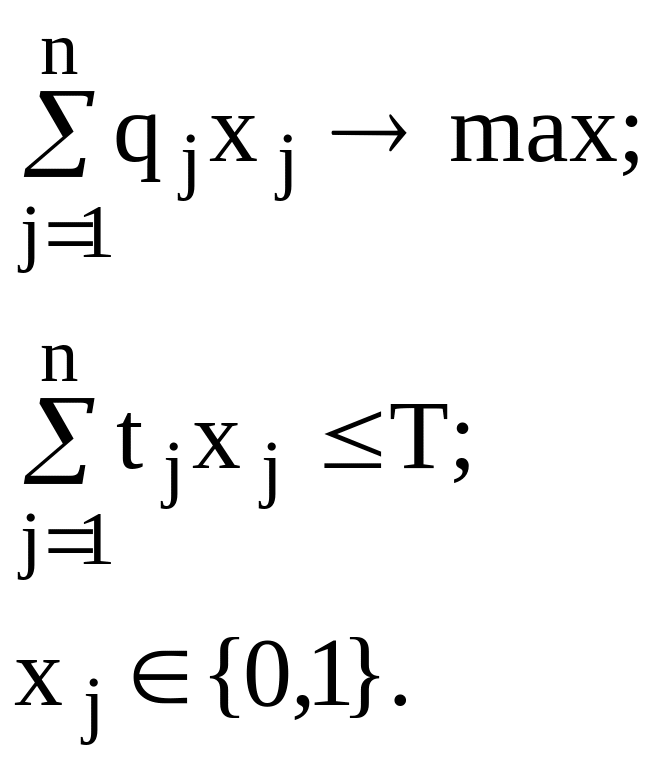

 A2
A2