2.4.Двойственность в линейном программировании

Каждой ЗЛП можно поставить в соответствие двойственную в соответствии с следующими правилами:

1) если целевая функция F исходной задачи стремится к минимуму, то целевая функция Ф двойственной задачи – к максимуму и наоборот;

2) число переменных двойственной задачи равно числу ограничений исходной, число ограничений двойственной задачи равно числу переменных исходной. Каждому i-му ограничению исходной задачи соответствует переменная y_i двойственной задачи (двойственная переменная), а каждой j-й переменной исходной задачи соответствует j-е ограничение исходной задачи;

3) коэффициентами при переменных целевой функции двойственной задачи являются правые части ограничений исходной задачи, а правыми частями ограничений двойственной задачи являются коэффициенты при целевой функии в исходной задаче;

4 ) матрица коэффициентов при двойственных переменных в системе ограничений двойственной задачи является транспонированной матрицей коэффициентов при переменных в ограничениях исходной задачи;

5) для удобства построения двойственных задач рекомендуется в исходной задаче ограничения-неравенства записывать со знаком “ ” при максимизации и со знаком “ ” при минимизации;

6) каждому i-му ограничению – неравенству исходной задачи соответствует в двойственной задаче условие неотрицательности (y_i0), а ограничению -равенству - переменная y_i произвольного знака;

7) неотрицательной переменной исходной задачи x_j0 соответствует в двойственной задаче j-е ограничение – неравенство, а произвольной переменной x_j - равенство. При этом если двойственная задача подлежит минимизации, неравенство записывается со знаком “ ”, а если двойственная задача подлежит максимизации – со знаком “ ”.

Р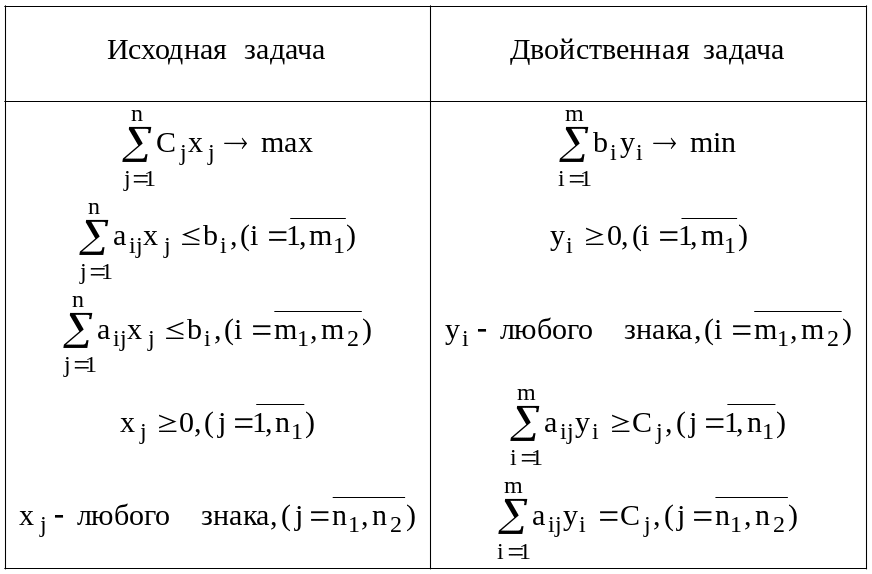 ассмотренные правила построения двойственных задач иллюстрируются табл. 8.

Таблица 8

Соотношение двойственности является взаимным, то есть задача двойственная по отношению к двойственной совпадает с исходной.

Пример Построить двойственную задачу к задаче определения производственного плана, приведенной в примере 1: определить, сколько продукции каждого вида x_j необходимо изготовить, чтобы при заданной прибыли от реализации единицы продукции c_j и заданных размерах имеющихся ресурсов b_i максимизировать общую прибыль.

Математическая модель задачи из примера 1 формулировалась следую-щим образом:

F=7x₁+3x₂+6x₃+12x₄max;

3x₁+x₂+2x₃+4x₄ 440;

x₁+8x₂+6x₃+2x₄ 200;

x₁+4x₂+7x₃+2x₄ 320;

x_j 0, j= .

Введя три двойственные переменные y₁ , y₂ , y₃ , в соответствии с приве-денными выше правилами построим двойственную задачу:

Ф=440у₁+200y₂+320у₃min;

3y₁+y₂+y₃ 7;

y₁+8y₂+4y₃ 3;

2y₁+6y₂+7y₃6;

4y₁+2y₂+2y₃ 12;

y_i 0, j= .

Отсюда видно, что двойственная задача заключается в определении стоимости единицы ресурса y_i, чтобы при заданных количествах ресурсов b_i и заданной прибыли c_j от реализации единицы продукции минимизировать общую стоимость ресурсов.

Пара взаимодвойственных задач, в которых все ограничения записываются в виде неравенств, причем при максимизации знаки всех неравенств , а при минимизации , называется симметричной. Приведенная выше пара задач симметрична.