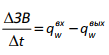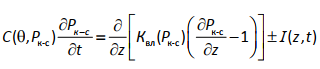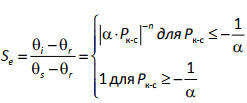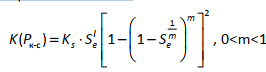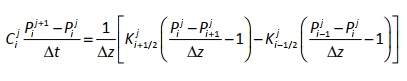Mat_mod_shpory
.docx|
МАТЕМАТИЗАЦИЯ НАУЧНОГО ЗНАНИЯ — процесс применения понятий и методов математики в естественных, технических и социально-экономических науках для количественного анализа исследуемых ими явлений. Хотя математизация научного знания началась давно, но только в период современной научно-технической революции приобрела большой размах и значение. Наряду с традиционными областями применения математики, какими являются механика, астрономия, физика и химия, ее методы стали проникать в такие отрасли науки, которые раньше считались не поддающимися математизации ввиду их особой сложности (биология, экономика, социология, лингвистика и др.). Как и любая другая модель, математическая модель, во-первых, отображает некоторые существенные свойства и отношения оригинала, во-вторых, в точно определенном смысле замещает его и, в-третьих, дает новую информацию о нем. Однако в отличие от материальных моделей они являются разновидностями концептуальных моделей, которые отображают количественно-структурные отношения исследуемых процессов и являются оперативно-символическими по характеру применения. Часто такое моделирование характеризуют как искусство применения математики, причем перевод существенных факторов исследуемых явлений на язык математики считают самой трудной стадией моделирования. Математизация почвоведения, интенсивно идущая последние 30 - 40 лет и несомненно являющаяся естественным результатом развития, с одной стороны, самого почвоведения, а с другой - математики и вычислительной техники, была предугадана гением В.В. Докучаева, связавшего превращение созданной им науки в точную с возможностью, в частности, преодоления тех трудностей, которые возникают в связи с необходимостью иметь дело с переменными величинами, трудно поддающимися "цифровому обозначению" (Докучаев, 1886). К мысли о статистической природе свойств почв почвоведы пришли давно и по крайней мере до того, как статистические методы анализа данных нашли применение в исследовании почв. Отражением этих представлений, например, явилась дискуссия по целесообразности использования смешанных образцов
СИСТЕМНЫЙ АНАЛИЗ – совокупность методов и средств, используемых при исследовании и конструировании сложных и сверхсложных объектов, прежде всего методов выработки, принятия и обоснования решений при проектировании, создании и управлении социальными, экономическими, человеко-машинными и техническими системами. Система - совокупность элементов, которая обладает следующими признаками:
Элемент - некоторый объект (материальный, энергетический, информационный), который обладает рядом важных для нас свойств, но внутреннее строение (содержание) которого безотносительно к цели рассмотрения. Структура - относительно устойчивая фиксация связей между элементами системы. Структуры делятся на простые и сложные в зависимости от числа и типа взаимосвязей между элементами. Целостность системы - это ее относительная независимость от среды и других аналогичных систем. Эмерджентность - несводимость (степень несводимости) свойств системы к свойствам элементов системы. Под поведением (функционированием) системы будем понимать ее действие во времени. Изменение структуры системы во времени можно рассматривать как эволюцию системы. Цель системы - предпочтительное для нее состояние. Целенаправленное поведение - стремление достичь цели. Обратная связь - воздействие результатов функционирования системы на характер этого функционирования. Если обратная связь усиливает результаты функционирования, то она называется положительной, если ослабляет - отрицательной. МОДЕЛЬ СИСТЕМЫ математический или физический аналог реальной системы, в котором характер протекания основных процессов подобен протеканию таких же процессов в реальной системе
Практически любой объект с определенной точки зрения может быть рассмотрен как система. Вопрос состоит в том, насколько целесообразна такая точка зрения.
Под математическим моделированием понимают описание в виде уравнений и неравенств реальных физических, химических, технологических, биологических, экономических и других процессов. Как методология научных исследований математическое моделирование сочетает в себе опыт различных отраслей науки о природе и обществе, прикладной математики, информатики и системного программирования для решения фундаментальных проблем. Математическое моделирование объектов сложной природы – единый сквозной цикл разработок от фундаментального исследования проблемы до конкретных численных расчетов показателей эффективности объекта. Результатом разработок бывает система математических моделей, которые описывают качественно разнородные закономерности функционирования объекта и его эволюцию в целом как сложной системы в различных условиях. Вычислительные эксперименты с математическими моделями дают исходные данные для оценки показателей эффективности объекта. Поэтому математическое моделирование как методология организации научной экспертизы крупных проблем незаменимо при проработке народнохозяйственных решений. (В первую очередь это относится к моделированию экономических систем).
Множество математических моделей можно разделить на две большие группы: аналитические модели, в которых для определения значения переменных состояния модели могут быть получены аналитические выражения, позволяющие для любых входных функций и начальных условий непосредственно определять значения интересующих нас величин, и имитационные модели, в которых ЭВМ является принципиально необходимым аппаратом исследования, так как значения переменных состояния модели рассчитываются по входным и начальным данным с помощь» набора математических операций, записанных в виде машинной программы. После того как модель исследована, возникает задача ее интерпретации, т.е. перевода утверждений, полученных относительно модели, на утверждения относительно системы-оригинала. Интерпретация модели не является строго однозначной, так как разобравшись в менее сложной системе, нужно применить полученные результаты к более сложной. Поэтому при разработке математических моделей почвенных процессов нужно помнить, что они должны быть хорошо интерпретируемы. переменные состояния (х1->переменные состояния->у1) – внутренние (промежуточные) переменные, совокупность которых полностью характеризует свойства системы; внешние переменные (х1) , характеризующие внешние воздействия на входы системы; контролирующие переменные (y1) представляющие те реакции на внешние воздействия и те состояния системы, которые интересны для исследователя. Математические уравнения - абстрактные формализованные представления закономерностей поведения реальной системы. (то что происходит в переменных состояниях) Параметры - условия в которых все происходит Постоянные константы- закономерности.
Под вычислительным экспериментом понимают создание и изучение математических моделей на ЭВМ. Необходимо изучить поведение, т.а. решить входящие в нее уравнения при различных значениях параметров, управляющих исследуемыми процессами. Модель должна быть доброкачественной т.е. правильно отражать те особенности изучаемых процессов, которые интересуют исследователя. Информация заложенная в модель, должна- быть надежной. Если модель реалистична, то исследователь получает возможность, проводя вычислительный эксперимент как бы изучать саму природу. Вычислительный эксперимент похож на обычный. На ЭВМ (экспериментальной установке) проводится серия расчетов (измерений), в результате которых исследователь получает совокупность чисел, описывающих поведение изучаемой системы. На заключительном этапе проводится анализ результатов, сопоставление их с данными натурных экспериментов и становится ясно, удачно ли выдрана модель. При необходимости она уточняется и "цикл" вычислительного эксперимента повторяется снова.
Важные особенности почвы как объекта моделирования: 1) высокая сложность и иерархичность строения, 2) незамкнутость, 3) влияние внешей среды, 4) целостность, 5) динамичность, 6) нестационарность, 7) инерционность, 8) нелинейность. Сложность. Современное генетическое почвоведение исходит из понятия о почве как об очень сложной структурной системе, состоящей из множества иерархических подсистем, и в свою очередь являющейся подсистемой в системе более высокого уровня - экосистеме. С математической точки зрения сложность строения системы означает, что ее нельзя описать каким-нибудь одним параметром. Описание ее состояния требует задания многих характеристик. На математическом языке это формулируется так: фазовое пространство системы многомерно. Открытость. Почва является открытой системой, т.е. находится в состоянии постоянного обмена веществом и энергией с округающей средой. Отсюда следует вывод о необходимости совместного моделирования как почвенных процессов, так и процессов в окружающей среде. Нелинейность. Нелинейность почвы обусловлена нелинейным характером подавляющего большинства ее внутренних и внешних связей. С нелинейностью почвы связаны значительные трудности при моделировании почвенных процессов. Все вышесказанное свидетельствует о том, что по сложности внутреннего строения и по количеству и разнообразии внутренних и внешних связей, почва относится к числу наиболее сложных природных систем, чем и обусловлены большие трудности, возникающие на пути математического моделирования в почвоведении. Иерархичность. Почва имеет структуру. Пространственно-временная гетрогенность. Почва разделена по времени и месту формирования, условиям. Сложный характер взаимодействия с окр.средой. Почва находится в непрерывном взаимодействии с окружающей средой. Это взаимодействие характеризуется большим числом разнообразных связей. Связи системы с внешней средой в целях анализа подразделяют на элементы, именуемые .факторами и условиями окружающей среды. Факторам среды свойственна динамичность, тогда как стабильные, не изменяющиеся во времени воздействия, называются условиями среды (Куркин, 1976). Многим связям почвы с окружающей средой свойственна динамичность, носящая крайне сложный характер. Следовательно окружающая среда, в которую "погружена" почва является полифакторной. Монодоминантность возникает, если один из факторов, находясь либо в максимуме, либо наоборот, в минимуме, оказывает на систему столь сильное влияние, что подавляет действие всех остальных факторов (низкая температура в тундре, недостаточная влагообесиеченность в сухих степях и т.п.). Синергизм - взаимоусиление действия на систему двух или более факторов. Например, высокий уровень залегания грунтовых вод и их высокая минерализация приводит к засолению почв. Антагонизм - взаимокомпенсация действия на систему двух или большего числа факторов. Например, влияние повышенной температуры на испарение влаги из почвы может быть в значительной степени компенсировано высокой относительной влажностью воздуха. Математическое следствие: модель почвы должна содержать много параметров, характеризующих полифакторную внешнюю среду, в которой она Функционирует.
Моделирование высвечивает пробелы в наших знаниях об исследуемой системе и следовательно модели могут играть важную роль в планировании новых наблюдений и экспериментов. Математические модели могут служить целям интеграции информации об изучаемой системе, так как позволяют связать в единое целое результаты отдельных локальных исследований, перевести их на единый математический язык и эффективно использовать при решении поставленной задачи. Очень часто модели строят с целью прогнозирования последствий тех или иных антропогенных воздействий на изучаемые системы.
По типу реализации модели различаются на реальные и идеальные/ К первой группе относятся натурные и аналоговые модели. Трудности, возникающие в работе с этими моделями, связаны с установлением степени их адекватности к системе оригиналу, а также часто носят технический характер. Идеальные модели подразделяются в свою очередь на концептуальные (словесные и графические) и математические модели, которые выражаются языком математических символов. Множество математических моделей можно разделить на две большие группы: аналитические модели, в которых для определения значения переменных состояния модели могут быть получены аналитические выражения, позволяющие для любых входных функций изначальных условий непосредственно определять значения интересующих нас величин, и имитационные модели, в которых ЭВМ является принципиально необходимым аппаратом исследования, так как значения переменных состояний модели рассчитываются по входным и начальным данным с помощь набора математических операций, записанных в виде машинной программы. Как аналитические, так и имитационные модели могут подразделяться на детерминированные и стохастические (вероятностные). В детерминированных моделях значения переменных состояния модели определяются однозначно с точностью до ошибок вычислений. В стохастических моделях для каждой переменной может быть получено распределение всех возможных значений, характеризуемое такими показателями как математическое ожидание, дисперсия и т.п. По характеру временного описания динамики переменных состояния модели различаются на дискретные и непрерывные. Дискретные модели описывают поведение системы в фиксированные моменты времени. В непрерывных моделях значения переменных состояния могут быть найдены для любого момента времени рассматриваемого интервала.
Имитационные модели имитируют реальность, при этом, как правило, эксперимент многократно повторяется. Имитационная модель —математическая модель изучаемой системы, предназначенная для использования в процессе машинной имитации. Она является по существу программой для компьютера, а эксперимент над ней состоит в наблюдении за результатами расчетов по этой программе при различных задаваемых значениях вводимых экзогенных переменных. Имитационное моделирование используется в случаях, когда применение математических аналитических моделей неадекватно или является слишком сложным. Хотя методы имитационного моделирования не слишком элегантны, они являются очень гибкими и мощными в применении. Они шаг за шагом воспроизводят процесс функционирования системы. Эта система может включать ряд стохастических переменных. В имитационном моделировании, как и в большинстве методов исследования операций, при построении моделей и их последующем анализе широко используются компьютеры. В этой области применение компьютеров становится особенно важным, поскольку значимую и обоснованную информацию из имитационной модели можно получить только после проведения расчетов для различных случайных чисел. Если мы заинтересованы в нахождении стационарного состояния модели, необходимо сделать расчет за длительный период моделируемой переменной времени и таким образом получить средние значения соответствующих статистических характеристик. Если же моделируемый период слишком мал, то на средние значения переменных могут оказывать воздействие начальные (стартовые) колебания. Термину регрессионная модель, используемому в регрессионном анализе, можно сопоставить синонимы: «теория», «гипотеза». Эти термины пришли из статистики, в частности из раздела «проверка статистических гипотез». Регрессионная модель есть прежде всего гипотеза, которая должна быть подвергнута статистической проверке, после чего она принимается или отвергается. Регрессионная модель объединяет широкий класс универсальных функций, которые описывают некоторую закономерность. При этом для построения модели в основном используются измеряемые данные, а не знание свойств исследуемой закономерности. Такая модель часто неинтерпретируема, но более точна. Это объясняется либо большим числом моделей-претендентов, которые используются для построения оптимальной модели, либо большой сложностью модели. Нахождение параметров регрессионной модели называется обучением модел Недостатки регрессионного анализа: модели, имеющие слишком малую сложность, могут оказаться неточными, а модели, имеющие избыточную сложность, могут оказаться переобученными. Примеры регрессионных моделей: линейные функции, алгебраические полиномы, ряды Чебышёва, нейронные сети без обратной связи, например, однослойный персептрон Розенблатта, радиальные базисные функции и прочее Минимальные (базовые) - минимально необходимый набор данных и формул. Не всегда отображают всю суть, но быстры в расчетах.
С математической точки зрения сложность строения системы означает, что ее нельзя описать каким нибудь одним параметром. Описание ее состояния требует задания многих характеристик. На математическом языке это формулируется так: фазовое пространство системы многомерно. Структурные модели описывают поровое пространство элементарного представительного объема почвы на двух уровнях - макроуровне, размеры которого сопо-ставимы с размерами почвенных горизонтов, и микроуровне, размеры которого сопоставимы с размерами структурных почвенных элементов. Модели водного и теплового режима почв.
Модель Динамическая - модель, имитирующая развитие процесса или поведение моделируемого объекта во времени. Статическая модель — математическая модель, в которой все зависимости отнесены к одному моменту времени. биогеохимические модели - пример цикл углерода (атмосфера-почва-растение), учитывает фазовые изменения веществ. Исследует, соответственно, в динамике. биоэнергетические модели - определение потока биогенных элементов и их накопления в биомассе в экосистеме модели динамики популяций позволяет изучить изменение популяции во времени (рост, колебания или падения численности, как пример) Динамическая структурная система должна отображать вход в систему, промежуточное состояние и выход. Позволяет отследить изменение одного фактора и его влияние на другие во времени. Fuzzy модели - модели, в которых берется интервал от одного значения до другого, а не два значения (т.е. берется не 0 и 1, а интервал от 0 до 1). Теория нечеткой логики – это раздел прикладной математики, посвященный методам анализа данных, характеризующихся высокой неопределенностью. Индивидуально ориентированное моделирование использует подход, в рамках которого основным объектом модели является индивид, представляющий собой уникальную, дискретную единицу, у которой есть некоторый набор характеристик, изменяющихся в течение жизненного цикла. Каждый из индивидов взаимодействует с другими индивидами. Модели этого типа строят «снизу вверх», начиная с элементов системы (индивидов). Модельер определяет поведение только индивидов, а общее поведение системы является результатом совокупной деятельности многих индивидов, каждый из которых следует своим собственным правилам взаимодействия со средой и другими индивидами. Целью моделирования в этом случае является понимание того, каким образом интегральные свойства системы возникают из множества локальных взаимодействий между ее элементами (индивидуумами). Искусственная нейронная сеть (ИНС) — математическая модель, а также её программное или аппаратное воплощение, построенная по принципу организации и функционирования биологических нейронных сетей. Для решения информационных и расчетных задач, анализа, моделирования, отображения обстановки и местности многочисленные пользователи применяют пространственные (трехмерные) модели местности. Вместе с электронными картами они являются составной частью картографического обеспечения имеющихся и создаваемых систем управления, информационно-расчетных систем. Стохастическая модель — такая экономико-математическая модель, в которой параметры, условия функционирования и характеристики состояния моделируемого объекта представлены случайными величинами и связаны стохастическими (т.е. случайными, нерегулярными) зависимостями, либо исходная информация также представлена случайными величинами. Следовательно, характеристики состояния в модели определяются не однозначно, а через законы распределения их вероятностей. Моделируются, например, стохастические процессы в теории массового обслуживания, в сетевом планировании и управлении и в других областях. При построении С.м. применяются методы корреляционного и регрессионного анализа, другие статистические методы. Экотоксикологические модели, описывают воздействие химических агентов на популяции и биоценоз. Гибридные системы — математические модели систем управления, в которых непрерывная динамика, порождаемая в каждый момент времени одной из априорно заданного набора непрерывных систем, перемежается с дискретными операциями, подающими команды либо на мгновенное переключение с одной системы на другую, либо на мгновенную перестройку с заданных текущих координат на другие координаты, либо на то и другое одновременно.
Любое исследование является процессом, предполагающим определенную последовательность операций, использования методов, оценки результатов предварительных, промежуточных и конечных. Это характеризует итерационное строение процесса исследования. Его успех зависит от того, как мы выберем эти итерации, как будем их комбинировать. Принцип соответствия сложности модели требуемой точности результатов моделирования. В общем плане проблема “точность - сложность” формулируется в виде одной из двух оптимизационных задач: - задается точность результатов моделирования, а затем минимизируется сложность модели; - имея модель определенной сложности, стремятся обеспечить максимальную точность результатов моделирования.
Для оценки моделей используют три основных показателя: реалистичность, точность и общность. Реалистичность это степень, с которой утверждения, полученные на основе модели, соответствуют нашим представлениям об изучаемой системе; Точность – количественная оценка степени совпадения модельных и экспериментальных результатов; Общность – область применимости модели, число различных ситуаций, которые модель отражает. Эти требования к моделям противоречивы. Повышение реалистичности и общности, как правило, сопровождается снижением точности. Поэтому приходится выбирать оптимальное соотношение этих показателей в соответствии с целями моделирования. Наглядность - не только особое свойство психических образов, но и свойство математического объекта в рамках определенного дидактического процесса. Таковым он становится, когда у статистически достоверной выборки обучаемых возникают наглядные перцептивные образы. Модульный принцип построения математических моделей (подсистем) позволяет использовать типовые решения на отдельных этапах проектирования, строить разветвленные и гибкие вычислительные схемы. Модели различаются по степени качественной и количественной адекватности исследуемому объекту относительно выбранных характеристик, по возможностям их исследования.
1 шаг – постановка задачи. На этом этапе формулируются основные вопросы, ответы на которые планируют получить с помощью модели. На первом этапе определяется проблема, для решения которой предполагается использовать метод моделирования. От выбора проблемы зависит успех всей работы, так как, с одной стороны, можно выбрать проблему, не поддающуюся решению методом моделирования, а с другой - взяться за проблему, для решения которой не требуется вся мощь этого метода. Определить проблему важно также для того, чтобы сконцентрировать ограниченные исследовательские ресурсы в заданном направлении. В соответствии с выбранной проблемой устанавливаются цели моделирования. Модели могут задумываться с разными целями: 1) для организации и четкого, наглядного представления ин‐ формации об изучаемом объекте в соответствии с изучаемой проблемой; 2) для определения исследовательских приоритетов и планирования экспериментов; 3) для определения роли и важности отдельных процессов по отношению к решаемой проблеме; 4) для проверки гипотез о взаимодействиях отдельных элементов и подсистем и характере функционирования системы; 5) для оценки устойчивости системы; 6) для прогноза поведения системы при изменении внутренних характеристик и внешних условий; 7) для выбора оптимального управления в соответствии с выбранным критерием; 8) для оценки рисков. 2 шаг – выбор объекта исследования и сбор данных. В соответствии с поставленными задачами выбирается объект исследования, и определяются его пространственные границы и временной масштаб. Также выясняется место изучаемой системы, как элемента в системе более высокого иерархического уровня. На этом этапе осуществляется первоначальный сбор данных об объекте исследования. 3 шаг – выбор типа модели На этом этапе выбирается тип модели, который позволяет решить поставленную задачу. С этой целью рассматриваются и сравниваются опубликованные ранее модели, направленные на решение подобных задач и оценивается качество собранной информации об изучаемой системе. Если данных достаточно для экспериментального обеспечения модели, то переходят к следующему этапу. В противном случае нужно проводить дополнительные исследования для получения недостающих данных, или выбирать такой тип модели, который может быть реализован на основании имеющихся данных. В последнем случае приходится возвращаться на первый этап и корректировать постановку задачи. 4 шаг – концептуализация модели Концептуальная модель представляет собой концептуальную структуру (систему взглядов) в рамках которой мы анализируем факты. Она отражает наши представления об изучаемой системе. Так как модель − всегда упрощение реальности, на этапе концептуализации выбирают компоненты и процессы, которые кажутся наиболее важными в свете рассматриваемой проблемы. На основе этого выбора определяют окружающую среду системы и характеризующие ее параметры, внутренний состав и структуру модели. Для сложных систем модель может иметь блочную (модульную) структуру, состоящую из ряда блоков, каждый из которых представляет одну из подсистем изучаемой системы. В этом случае на этапе концептуализации формулируют гипотезы о взаимодействии блоков. Блочный принцип построения модели позволяет описать процессы с разными характерными временами, так как для каждого блока можно выбрать свой временной шаг. Этот подход позволяет заменять отдельные блоки и использовать блоки из одних моделей при конструировании других 5 шаг – формализация модели Формализация модели – это представление системы в форме совокупности математических соотношений, описывающих ее поведение и свойства. Задачей этого этапа является переход от качественной структуры модели, которая только устанавливает наличие или отсутствие связей между переменными, к математической (аналитической) структуре, устанавливающей конкретный вид зависимостей между переменными состояния и внешними переменными модели. При этом опираются на уже известные за‐ коны, результаты статистического анализа экспериментальных данных, экспертные оценки и гипотезы о характере связей между переменными. 6 шаг – выбор метода решения Методы решения можно разделить на аналитические и алгоритмические. В первом случае результат представляет собой аналитическое выражение или их совокупность. Аналитические методы более удобны для последующего анализа результатов, но применимы лишь для относительно простых моделей. Если поставленная задача хотя бы в упрощенном варианте допускает аналитическое решение, его обязательно следует получить. Прежде чем пользоваться ЭВМ, задачу необходимо всесторонне исследовать аналитическими методами. Аналитические методы – «старое, но грозное оружие» − не теряют своего значения. 7 шаг – реализация математической модели Реализация модели – получение, если это возможно, решения в аналитической форме или разработка компьютерной про‐ граммы для реализации численного метода решения. Большинство программ, реализующих математические модели, состоят из трех основных частей: 1. подготовка и проверка исходных данных модели; 2. решение задачи (реализация вычислительного алгоритма); 3. отображение полученных результатов (в числовом, графическом или текстовом виде). 8 шаг – верификация модели Верификация – это проверка того, что включенные в модель формальные соотношения правильно отражают выбранную концепцию, что они не имеют внутренних противоречий и несоответствий в размерности, что предусмотренные математические пре‐ образования не содержат ошибок и программа составлена правильно. Прежде чем переходить к работе с моделью, необходимо убедиться в ее корректности и правильном функционировании всех алгоритмов и программ модели. Для этого нужно выполнить отладку программы и провести независимое тестирование. 9 шаг – анализ чувствительности На этом этапе проверяют чувствительность переменных состояния модели к изменениям начальных условий, параметров, структуры модели, внешних переменных и управляющих функций. Это позволяет выявить переменные с высокой и низкой чувствительностью, а так же от каких параметров и внешних переменных сильнее всего зависит поведение модели. Анализ чувствительности помогает определить ключевые моменты функционирования системы в контексте изучаемой проблемы и установить исследовательские приоритеты. Он показывает пути совершенствования модели, путем уточнения ее параметров и изменения структуры. Результаты анализа чувствительности полезны при верификации, калибровке и проверке модели. Известно много различных методов анализа чувствительности, которые классифицируют как математические и графические. 10 шаг – калибровка (подбор значений параметров) Калибровка – это попытка найти лучшее соответствие между расчетными и наблюдаемыми данными путем варьирования значений некоторых параметров. Для некоторого набора значений параметров вычисляются значения переменных состояния, которые сравниваются с их экспериментальными оценками. Выбирают тот набор значений параметров, который дает наименьшие расхождения с экспериментальными значениями. 11 шаг – проверка адекватности модели Под адекватностью математической модели понимается степень соответствия результатов моделирования экспериментальным данным, характеризующим изучаемую систему. Проверка должна осуществляться по независимым данным, не использовавшимся при калибровке модели. 12 шаг − заключительный синтез Моделирование сложных динамических систем никогда не бывает полностью завершенным. На каждом из этапов моделирования могут возникать трудности, для преодоления которых необходимо корректировать модель. Например, расширять спи‐ сок переменных состояния, уточнять вид функций, используемых для описания взаимодействий между переменными, уточнять значения параметров и др. Разработка модели итеративный процесс, обеспечивающий ее постоянное обновление и развитие, результатом которого являются новые знания об изучаемой системе
Источники неопределенностей в моделях Так как модель всегда является упрощенным представлением реальности, любое предсказание имеет неопределенность.Неопределенности обусловлены, как природной вариабельностью моделируемых явлений, так и ошибками, сделанными в процессе определения качественной и аналитической структуры модели, при оценке параметров и выборе ситуаций, для которых модель будет реализована. Ошибки, возникающие на разных этапах построения и реализации модели не являются независимыми, а могут взаимодействовать самым неожиданным образом, увеличивая неопределенность предсказаний. Источники неопределенностей в моделях Природная вариабельность -> Структура модели - Выбор сценария - Входы и параметры - Прогнозы Ошибки, возникающие при определении структуры модели При определении структуры модели возникает проблема выбора числа компонентов модели. Оно зависит от цели моделирования и выбранного масштаба. Нужно помнить, что ошибки динамических моделей заметно возрастают уже при агрегировании переменных, различающихся по скоростям оборота более чем в три раза. Выбор уровня сложности модели, который минимизирует ошибки предсказаний, является непростой задачей, так как при увеличении детальности описания особенно за счет включения процессов, параметры которых трудно измерить, возрастает неопределенность модельных предсказаний. Лучшим подходом в этих обстоятельствах является построение серий последовательно усложняющихся моделей. Этот способ реализует два методологических принципа системного анализа: принцип итеративности, состоящий в последовательном совершенствовании модели, и принцип соответствия сложности и точности. В результате построения серии получают модель минимальной сложности для заданной точности экспериментальных данных. Ошибки, возникающие при выборе сценария Неопределенность модельных предсказаний значительно возрастает, когда модели применяются к областям большим, чем их внутренний масштаб. Например, когда локальные (точечные) модели, при построении которых исходили из предположения о гомогенности климатических и почвенных условий в пределах единичной площади, применяются в региональном масштабе. В этом случае важно оценить как отказ от предположения о пространственной однородности внешних условий сказывается на ошибках моделирования. Как известно, для нелинейных функций значение функции, определенное по среднему значению аргумента не равно среднему значению функций, определенных раздельно для каждого из значений аргументов. Следовательно, ошибки моделирования при переходе от локального к региональному масштабу будут возрастать в тех случаях, когда модель содержит нелинейные функции от изменяющихся в пространстве входных переменных. Ошибки агрегирования зависят не только от степени нелинейности, используемых в модели функций, но и от пространственного масштаба агрегирования. Ошибки, связанные с оценкой параметров Для исследования зависимости предсказаний от точности значений параметров широко применяется анализ чувствительности. Показатели чувствительности представляют собой производную интересующего модельного предсказания (переменной отклика) по параметру. Анализ чувствительности позволяет выявить параметры, к которым переменная отклика наиболее чувствительна. Для уменьшения ошибок моделирования эти параметры следует определять наиболее точно. Анализ чувствительности показывает также путь усложнения модели в тех случаях, когда ее адекватность недостаточна. Усложнять модель целесообразно путем уточнения описания тех процессов, к параметрам которых модель наиболее чувствительна. Исследование неопределенности предсказаний позволяет определить пути совершенствования моделей.
Статические модели не рассматривают изменения системы во времени. Статические биогеохимические модели относятся к классу компартментальных концептуально-балансовых моделей, отражающих законы сохранения вещества. Основы методологии построения таких моделей заложены в работах Г. Одума(1961), Дж. Форрестера (1961), А.А. Ляпунова и Яблонского (1963), А.А. Ляпунова и А.А. Титляновой (1971), Н.И.Базилевич (1978). Статические модели характеризуют усредненные по времени ситуации. При построении таких моделей система разбивается на блоки (компартменты), содержащие определенные запасы вещества и обменивающиеся им между собой и окружающей средой. На основе экспериментальных данных определяются запасы вещества в выделенных блоках, скорости обмена между ними, а также скорости входных и выходных потоков. Модель представляют в виде численной потоковой диаграммы с указанием запасов и скоростей потоков. Достоинства статических биогеохимических моделей При их построении, как правило выявляют недостаточно изученные звенья круговорота вещества в экосистемах, что позволяет использовать их как эффективный инструмент планирования исследований. Такие модели, несмотря на их схематичность и известную условность, могут быть полезны для описания квазистационарных состояний или для описания усредненной по времени ситуации. Они могут служить эталоном - точкой отсчета для мониторинга окружающей среды. Недостатки Статический характер, они отражают только среднюю картину круговорота вещества в экосистемах за определенный временной интервал. Энвирон-анализ В конце 70-х - начале 80-х годов прошлого века был предложен метод анализа компартментальных моделей, получивший название энвирон-анализа. ЭНВИРОН - совокупность тех блоков и потоков между ними, с которыми рассматриваемый блок связан либо непосредственно, либо через другие блоки. ВХОДНОЙ ЭНВИРОН - совокупность блоков, выходы из которых рано или поздно поступят на вход рассматриваемого блока вместе с соответствующими потоками. ВЫХОДНОЙ ЭНВИРОН - совокупность блоков, в которые рано или поздно поступит частица вещества, прошедшая через рассматриваемый блок вместе с соответствующими потоками. Используя матричные соотношения этого метода, можно вычислить, какая доля выходящего из i-го компартмента потока попадает в j-й, оценить среднее время, проводимое веществом в компартменте, сделать количественные выводы о роли того или иного процесса в функционировании экосистемы. Энвирон-анализ предлагает исследование только лишь стационарного состояния системы, поскольку одним из его исходных требований является постоянство потоков и запасов вещества.
Динамическими системами называют любые системы (физические, химические, биологические, экономические, социальные и.др.), состояние которых изменяется во времени дискретно или непрерывно. В математическом понимании динамической системой является любой объект, для которого однозначно определено понятие состояния, как совокупности некоторых величин в данный момент времени, и задан закон, который описывает изменение начального состояния с течением времени. Почва относится к динамическим системам. Функционирование почвы, как целостной системы, является результатом взаимодействия составляющих ее компонентов. Понять динамические свойства почвы можно на основе системного подхода, анализируя поведение каждого из ее компонентов, как результат его взаимодействия с другими компонентами. Одним из наиболее эффективных методов изучения изменений почв с течением времени является построение и анализ динамических моделей. Анализ динамических свойств моделей, характеризующих разные аспекты функционирования почв, позволяет лучше понять особенности ее динамики. Для описания динамических систем используются различный математический аппарат (дифференциальные уравнения, дискретные отображения, теория марковских цепей и др.). В настоящем курсе мы рассмотрим динамические модели, представленные дифференциальными уравнениями. Математический язык дифференциальных уравнений для описания динамических систем был предложен Исааком Ньютоном (1642-1727). В настоящее время он широко используется при построении моделей в самых разных областях науки. Для того чтобы определить динамическую систему, модель которой мы хотим построить, нужно задать конечное число переменных, однозначно характеризующих ее состояние. Предположим, что в соответствии с поставленной проблемой, для характеристики состояния почвы выбрано n различных компонентов. Каждый i компонент характеризуется переменной состояния xi. В качестве переменных состояния могут быть выбраны концентрации различных веществ, численность микроорганизмов, и др. Закон изменения динамической системы во времени можно в общем виде представить системой n дифференциальных уравнений: (1)
Где xi – переменные состояния ; fi -известные функции; t -время Особый интерес представляет случай системы (1), когда правые части не зависят явно от переменной t: (2)
такие системы называются автономными. Динамические модели этого вида получили широкое распространение в почвоведении и экологии . Решение системы представляет собой совокупность функций, характеризующих зависимость переменных состояния от времени: х 1(t), х 2(t),….. х i(t),….. х n(t) (3) Лишь для небольшого класса систем дифференциальных уравнений удается найти аналитическое решение, то есть представить зависимость переменных состояния от времени в виде явно заданных математических формул. В большинстве случаев получают только численное решение. В процессе изменения состояния системы во времени переменные хi изменяются согласно системе уравнений (2). В момент времени t каждому состоянию системы соответствует совокупность n значений переменных хi(t). Для удобства анализа поведения динамических систем во времени используют понятие n- мерного фазового пространства - абстрактного пространства с осями координат х1, х2,... хi,… хn.. Тогда состояние динамической системы в каждый момент времени можно представить в виде точки этого пространства. Каждая точка Х этого пространства с координатами х1, х2,... хi,… хn соответствует определенному состоянию системы. Точка X(х1, х2,... хi,… хn) называется изображающей или фазовой точкой. Изменение состояния системы сопоставляется с перемещением изображающей точки в фазовом пространстве. Пусть в начальный момент времени t=t0 координаты изображающей точки X0(х10, х20,... хi0,… хn0). В каждый следующий момент времени t изображающая точка будет двигаться в соответствии с системой уравнений (2) и принимать положения X(х1, х2,... хi,… хn), соответствующие значениям х 1(t), х 2(t),… х i(t),….. х n(t). Линия, по которой движется изображающая точка в фазовом пространстве, называется фазовой траекторией. На фазовой траектории стрелками отмечается направление движения изображающей точки. Совокупность фазовых траекторий при различных начальных значениях переменных состояния представляет собой фазовый портрет системы. Характер фазовых траекторий отражает общие качественные черты поведения системы во времени. При рассмотрении динамических характеристик модели в первую очередь определяют ее стационарные состояния. В стационарном состоянии все производные по времени (i = 1…,n) в левых частях системы (2) обращаются в нуль. Приравнивая к нулю правые части системы уравнений (2), получим систему алгебраических уравнений (4) для определения стационарных значений переменных состояния : Начнем знакомство с динамическими моделями с самого простого случая, когда система описывается одним дифференциальным уравнением первого порядка вида: (5)
Стационарное состояние системы. В стационарном состоянии значения переменных в системе не меняются со временем. Это означает, что: (6) Следовательно f(x)=0. Корни алгебраического уравнения (6) являются стационарными состояниями системы (5).
Предположим, что скорость изменения значения переменной состояния пропорциональна самому ее значению:
Эта простая линейная модель демонстрирует одно из важнейших свойств математических моделей — их универсальность, т. е. их применимость к объектам принципиально различной природы. Поиск аналитического решения дифференциального уравнения.
Пример: Модель Мальтуса (модель экспоненциального роста численности популяции). Модель предложена Мальтусом (1766-1834) в 1798 г. в его классической работе «О законе роста народонаселения». Мальтус –известный английский демограф и экономист, обратил внимание на тот факт, что численность популяции растет по экспоненте ( в геометрической прогрессии), в то время как производство продуктов питания растет линейно ( в арифметической прогрессии), из чего сделал справедливый вывод, что рано или поздно экспонента обязательно обгонит линейную функцию и наступит голод. В основу модели положено простое утверждение, что скорость изменения численности населения со временем t пропорциональна его текущей численности x(t), умноженной на сумму коэффициентов рождаемости и смертности :
Введем параметр , который является показателем удельной скорости роста и получим: Решением
уравнения (9) является функция:
где x0 =x(t=0) -начальная численность. Эта модель не учитывает зависимости сложнейшего процесса изменения численности населения от множества условий и подходит только для описания изменения численности изолированной популяции, которая развивается в условиях неограниченных ресурсов. Например, динамики популяции простейших организмов, выращиваемых в культиваторе в условиях избытка пищи Экспоненциальный рост. Зависимость численности популяции от времени
Модель экспоненциального роста (9) используется для описания широкого круга явлений (радиоактивный распад, динамика популяций, разложение растительных остатков, минерализация гумуса, рост зарплаты и др.). На первый взгляд кажется, что между ними нет ничего общего. Однако описание всех этих разнородных явлений основано на одном общем предположении, что скорость изменения значения переменной состояния пропорциональна самому ее значению. Это предположение используется в различных областях знаний, а приведенный пример демонстрирует универсальность моделей, то есть их применимость для описания объектов различной природы. Простейшая линейная динамическая модель открытой системы В качестве еще одного примера динамической модели рассмотрим простейшую линейную модель открытой системы, в которой происходит обмен веществами «а» и «b» с окружающей средой и обратимая реакция первого порядка превращения a↔b.
Где «а» и «b» -переменные состояния, характеризующие концентрации этих веществ в системе; А,B – постоянные концентрации этих веществ во внешней среде; k1,k+2, k-2, k3 – константы скоростей процессов. Динамическая модель для этой системы имеет следующий вид:
Так
как по определению в стационарном
состоянии скорость изменения переменных
а
и b
равна 0, следовательно, производные
и , то приравнивая к 0
правые части (10), найдем стационарные значения а и b.
Они не зависят от начальных условий, то есть от значений переменных a и b в момент времени t=0. Это означает, что при каком бы начальном состоянии система не находилась, в ней со временем установится стационарный режим. Хотя начальные условия не влияют на стационарные значения, они определяют характер кривых, описывающих изменения переменных состояния при переходе от начального состояния при t=0 к стационарному при t→∞. На примере этой модели А.Б Рубин (1998) показал, что даже такая, до предела упрощенная, модель отражает основные черты совокупности метаболических реакций клетки как открытой системы. Она может быть использована для описания обменных процессов и в других открытых системах, например, в почве, что является еще одной демонстрацией универсальности математических моделей. Если модели, описывающие различные объекты, основаны на одинаковых предположениях, то для их описания могут быть использованы одни и те же математические выражения. Как отмечал великий французский математик Анри Пуанкаре : "Математика - это искусство давать разным вещам одно наименование".
Помочь получить
модель системы, содержащую наименьшее
число переменных состояния и параметров,
и в то же время правильно отражающую
ее основные свойства, представляющие
интерес в соответствии с поставленными
задачами, может учет
временной иерархии изучаемых процессов.
Принимая
во внимание характерные времена
изучаемых процессов, можно разделить
переменные состояния исходной модели
на «быстрые», «средние» и «медленные».
Предположим, что исходная модель
описывает динамику трех переменных
с различными характерными временами:
Причем Пусть мы наблюдаем за переменной y . Тогда за время Ty совсем медленная переменная z практически не будет изменяться и ее можно считать постоянным параметром, обозначим его z*. В этом случае исходную систему можно представить следующим образом:
Рассмотрим
теперь уравнение для х.
Эта «быстрая»
переменная
за время Ty
успеет достичь стационарного значения.
Поэтому для нее дифференциальное
уравнение можно заменить алгебраическим:
Таким
образом, благодаря учету иерархии
времен систему трех дифференциальных
уравнений удается свести к одному
дифференциальному уравнению:
В химии метод такого упрощения системы носит название метода квазистационарных концентраций (КСК). Обычно он применяется для систем химических реакций, промежуточные продукты которых являются частицами с высокой реакционной способностью (каталитические, ферментативные , биохимические процессы).
Динамические-учитывают
изменения и в пространстве и во времени.
Бывают точечные (дифф уравнения) и
пространственные (уравнения в частных
производных). Коротко-временая шкала
– часы, сутки, сезоны (м/о, ОВП, влажность);
средне-временная – десятки, сотни
лет; долго-временная – сотни, тысячи
лет. Учет временной иерархии процессов
позволяет сократить число дифференциальных
уравнений. «Совсем
медленные»
переменные (z)
не меняются на временах рассматриваемых
процессов, и их можно считать постоянными
параметрами. Для «быстрых» переменных(х)
можно вместо дифференциальных уравнений
записать алгебраические уравнения
для их стационарных значений, поскольку
«быстрые»
переменные достигают своих стационарных
значений практически мгновенно по
сравнению с «медленными»
(y).
Пусть имеется три группы переменных
с различными характерными временами:
dx/dt=P(x,y,z),
dy/dt=Q(x,y,z),
dz/dt=F(x,y,z),
переменные изменяются с разными
характерными временами, причем
Tx<<Ty<<Tz.
Пусть мы наблюдаем за переменной y,
характерное время изменения которой
– Ty.
Тогда за время Ty
«совсем медленная» переменная z
практически не будет изменяться, и ее
можно считать постоянным параметром,
обозначим его z*. Система дифференциальных
уравнений с учетом этого обстоятельства
будет содержать два уравнения и может
быть записана в виде: dx/dt=P(x,y,z*),
dy/dt=Q(x,y,z*).
Отметим, что z*
не является истинно стационарным
значением, «медленная» переменная z
будет продолжать меняться и «вести»
за собой более быстрые переменные x
и y.
В этом смысле медленная переменная
является ведущей, или «параметром
порядка». Рассмотрим теперь уравнение
для x.
Эта «быстрая» переменная изменяется
значительно быстрее, чем y,
и за время Ty
успеет достичь своего стационарного
значения. Значит, для переменной x
дифференциальное уравнение можно
заменить алгебраическим: P(x,y,z*)=0
или
В случае сложных динамических моделей с большим числом переменных состояния, отражающих нелинейные взаимодействия в почвах и экосистемах, возникают серьезные математические трудности в поиске аналитических решений, если их вообще можно получить. В то же время, методы качественной теории дифференциальных уравнений позволяют определить важные динамические свойства системы, не прибегая к поиску решения системы уравнений. Качественное исследование системы дифференциальных уравнений эффективно тогда, когда нужно предсказать характер динамического поведения системы и нет необходимости в поиске точного решения уравнений, поскольку начальные условия, значения внешних переменных и параметров системы сильно варьируют и не могут быть точно заданы. Именно с такой ситуацией обычно приходится сталкиваться при решении проблем почвоведения и экологии. Основоположники качественной теории дифференциальных уравнений: французский математик Анри Пуанкаре (1854-1912), русский математик Александр Михайлович Ляпунов (1857-1918). Качественное исследование динамических моделей дает хорошие результаты при исследовании моделей, представленных небольшим числом дифференциальных уравнений. Поэтому прежде чем приступить к качественному исследованию модели необходимо сократить число уравнений в исходной модели, оставив только те, которые отражают наиболее важные динамические свойства системы. Проводить редукцию количества уравнений модели нужно очень осторожно, так как есть риск потерять важные характеристики моделируемой системы и не только обеднить модель, но и сделать ее вообще неадекватной.
В первую очередь нас будут интересовать два вопроса: Как найти стационарные состояния? Как определить их устойчивость? Рассмотрим модель с одной переменной состояния, динамику которой описывает одно дифференциальное уравнение первого порядка: dx/dt=f(x). Пусть f(x) - - аналитическая функция. Найдем стационарные (особые) точки, обозначив их x̅. По определению, в этих точках dx/dt=0. следовательно, из условия f(x)=0 определим стационарные значения x̅. Наиболее важным свойством стационарного состояния является его устойчивость. В математике существуют разные определения понятия устойчивость. В дальнейшем мы будем использовать одно из основных – устойчивость по Ляпунову. Устойчивость определяется способностью системы самопроизвольно возвращаться в стационарное состояние после внешнего возмущения, выводящего систему из стационарного состояния. Стационарное состояние системы называется устойчивым, если при достаточно малом отклонении от стационарной точки система никогда от нее далеко не уходит. Если при выходе из стационарного состояния система удаляется от него, то оно является неустойчивым Стационарное состояние устойчиво, если достаточно малое возмущение всегда остается малым.Стационарное состояние называется неустойчивым, если малое отклонение со временем увеличивается. Стационарное состояние называется асимптотически устойчивым, если малые отклонения от него со временем затухают.
Александром Михайловичем Ляпуновым был предложен аналитический метод определения устойчивости стационарных состояний, приложимый к широкому классу систем дифференциальных уравнений. Суть метода состоит в следующем. Рассмотрим простую динамическую модель: dx/dt=f(x). Пусть система отклонилась от стационарного состояния x̅ и перешла в соседнюю с ним точку x̅+ γ, где γ -малое отклонение от стационарного состояния такое, что γ/x̅<<1. Перейдем от переменной х к переменной γ, получим: d(x̅+γ)/dt=dγ/dt=f(x̅+γ). Разложим стоящую в правой части этого уравнения функцию f(x̅+γ) в ряд Тейлора в точке x̅. dγ/dt=f(x̅)+f’(x̅)γ+1/2f”(x̅)γ2+… Принимая во внимание, что f(x̅)=0 и вводя обозначения a1=f’(x̅), a2=0.5*f”(x̅) перепишем выражение в виде: dγ/dt=a1γ+a2γ+… Отбросим нелинейные члены в этом уравнении как величины более высокого порядка малости и получим линейное уравнение:dγ/dt=a1γ. Это уравнение называется линеаризованным или уравнением первого приближения. Решение линеаризованного уравнения находится сразу: γ(t)=Ceλt где С – произвольная постоянная, λ=a1=f’(x̅). Если λ<0, то при t→∞ γ →∞, а следовательно первоначальное отклонение от стационарного состояния самопроизвольно затухает в силу характера поведения нашей системы. Таким образом стационарное решение рассматриваемого уравнения устойчиво по Ляпунову. Наоборот, если λ>0, то t→∞ γ →∞ и стационарное состояние неустойчиво. Если λ=0, то уравнение первого приближения не может дать ответа на вопрос об устойчивости стационарного состояния системы. Необходимо рассматривать члены более высокого порядка в разложении Тейлора. Аналогичные рассуждения приводятся при рассмотрении устойчивости стационарного состояния более сложных динамических систем. Метод Ляпунова позволяет по знаку производной правой части исходного уравнения получить ответ на вопрос об устойчивости его стационарных состояний. Качественное исследование логистической модели Логистическая модель была впервые предложена бельгийским математиком Пьером Франсуа Ферхюльстом (1804-1849) для описания численности населения в условиях ограниченности ресурсов, поэтому в его честь получила название модель Ферхюльста. В основе логистической модели лежат следующие предположения: существует предельная численность популяции К, которую может обеспечить окружающая среда. Параметр К характеризует «емкость среды»; скорость изменения численности популяции пропорциональна самой численности, умноженной (в отличие от модели Мальтуса) на величину отклонения от предельного значения. Модель Ферхюльста имеет следующий вид: dx/dt=qx(1-x/K). Начнем исследование с поиска стационарных значений численности популяции. Из условия: dx/dt=qx(1-x/K)=0 получим два стационарных значения: x̅1=0. x̅2=K. Определим их устойчивость. В соответствии с аналитическим методом определения устойчивости Ляпунова для этого нужно определить знак производной функции f(x) в стационарных точках. Производная равна: f(x)=(qx-q*x2/K)=q-2qx/K. Большинство реальных процессов и соответствующих им математических моделей нелинейны. Линейные модели отвечают частным случаям и, как правило, служат лишь первым приближением к реальности. Например, модели динамики популяций сразу становятся нелинейными, если принять во внимание ограниченность доступных популяции ресурсов. Они основаны на предположении о предельной численности популяции. Эта величина, называемая емкостью экологической ниши популяции, определяется ограниченностью пищевых ресурсов, мест для гнездования, и многими другими факторами, которые могут быть различными для разных видов. Заметим, что предположения о механизмах насыщения используются при построении многих моделей в различных областях знаний. Впервые ограничиненный рост популяции описал Ферхюльст в логистической модели в 1838 году: dx/dt=qx(1-x/K). Подставим стационарные значения: f(x̅1)=q-2qx/K|x=x̅1=q. Показатель удельной скорости роста q величина положительная. Следовательно стационарное состояние x̅1=0 неустойчиво. В точке x̅2=K производная отрицательна, f(x̅2)=q-2qx/K|x=x̅2=-q а значит, стационарное состояние x̅2=K является устойчивым. Логистическое уравнение допускает аналитическое решение, которое имеет следующий вид: x(t)=(x0Keqt)/(K-c(1-eqt) Нелинейная
модель Ферхюльста более реалистично
отражает динамику численности популяции
в сравнении с линейной моделью Мальтуса.
Как и в предыдущих примерах логистическая
модель демонстрирует универсальность
математических моделей, так как широко
используется не только для описания
динамики численности популяций, но и
во многих других случаях при описании
механизмов насыщения.
Критерий Ляпунова для системы из 2-ух уравнений. Рассмотрим характер поведения переменных при некотором небольшом отклонении системы от состояния равновесия. Введем
вместо переменных x, y новые независимые
переменные ξ, η, определив их как
смещения относительно равновесных
значений переменных, т.е. x=x̅+ξ;
y=y̅+η.
Теперь проделаем следующую операцию,
подставим выражения в уравнения
dx/dt=P(x,y)
и dy/dt=Q(x,y)
соответственно, получим: dx̅/dt+dξ/dt=P(x̅+ξ,
y̅+η)
и dy̅/dt+dη/dt=Q(x̅+ξ,
y̅+η),
dx̅/dt=dy̅/dt=0,
так как x̅
и y̅
- координаты особой точки. Теперь
разложим как и в случае одного уравнения,
правые части полученных уравнений в
ряд Тейлора соответственно по переменным
ξ и η, отбросим нелинейные члены.
Получим систему линеризованных о
уравнений: dξ/dt=aξ+bη,
dη/dt=cξ+dη,
где коэффициенты a,
b,
c,
d
суть значения частных производных в
точке (x̅,y̅),
т.е. a=P’x(x̅,y̅),
b=
P’y(x̅,y̅),
c=Q’x(x̅,y̅),
d=
Q’y(x̅,y̅).
Вернемся к нашим линейным уравнениям,
общее решение системы находим следующим
образом: ξ=Aeλt,
η=Aeλt,
подставив эти выражения в dξ/dt=aξ+bη,
dη/dt=cξ+dη,
в получившемся выражении сократим на
eλt,
в итоге получим λA=aA+bB;
λB=cA+dB.
Получившаяся система уравнений с
неизвестными А
и В
имеет, как известно, ненулевое решение
лишь в том случае, если ее определитель,
составленный из коэффициентов при
неизвестных, равен нулю:{(a-λ)/c}+{b/(d-λ)}=0
Раскрыв определитель, получим так
называемое характеристическое
уравнение системы: λ2-(a+d)λ+(ad-bc)=0,
решение этого уравнения дает значения
показателя λ1,2,
при которых ненулевые для А
и В
решения системы: λ1,2=(a+b)/2+√((a+b)2/4+bc-ad).
Если подкоренное выражение отрицательно,
λ1,2
– комплексно-сопряженные числа.
Предположим, что оба корня уравнения
λ2-(a+d)λ+(ad-bc)=0
имеют отличные от нуля действительные
части и что нет кратных корней. Тогда
общее решение системы dξ/dt=aξ+bη,
dη/dt=cξ+dη,
записанное в виде ξ=Aeλt,
η=Aeλt,
можно представить линейной комбинацией
экспонент с показателями λ1
и λ2:
ξ=С11eλ1t+
С12eλ2t,
η= С21eλ1t+
С22eλ2t. Подведем итоги, в случае если ad-bc≠0 возможны 6 типов состояния равновесия в зависимости от характера корней характеристического уравнения: 1.утойчивый узел (λ1 и λ2 действительны и отрицательны); 2.неустойчивый узел (λ1 и λ2 действительны и положительны); 3.седло (λ1 и λ2 действительны и имеют разные знаки); 4.устойчивый фокус (λ1 и λ2 комплексны и Reλ<0); 5.неустойчивый фокус (λ1 и λ2 комплексны и Reλ>0); 6. центр (λ1 и λ2 – мнимые). Re – это действительная часть комплексного числа, мнимая часть комплексного числа – Im.
Нелинейные динамические системы - может быть несколько стационарных состояний, переходов, разный характер поведения. Возникают периодически стационарные состояния и автоколебания (когда колебания вызваны внутренними взаимодействиями), меняется амплитуда колебаний, очень чувствительны к начальным состояниям.
Пространстве, к которому приближается траектория после затухания переходных процессов. Катастрофа-резкие изменения переменных состояний автоколебания atractor катастрофа системы, вызванные малыми возмущениями параметров, качественная перестройка сист. при малом изм. Параметров Бифуркация( ветвление) динамических систем dx/dt=F(x,α), где х-вектор параметров состояния системы(х1,х2,х3), а α-вектор параметров. F(x,α)=0, ищем стационарное состояние. x̅ (α), α*-бифуркационное значение α, то есть такое α, при котором в системе происходит качественная перестройка. Аттра́ктор — компактное подмножество фазового пространства динамической системы, все траектории из некоторой окрестности которого стремятся к нему при времени, стремящемся к бесконечности. «Детерминированный хаос», - режим с очень изменчивой амплитудой колебаний. Было показано, что в нелинейных моделях с числом степеней свободы больше двух при определенных критических значениях их внутренних параметров решение системы ведет себя как случайная функция. Поэтому для обозначения этого явления были предложены термины динамическая стохастичность и динамический (или детеминированный) хаос. Математическим образом установившихся режимов является притягивающее множество в фазовом пространстве или аттрактор (от английского to attract – притягивать). Простейший тип аттрактора представляет собой устойчивую особую точку, к которой стремятся фазовые траектории. Режиму устойчивых колебаний системы с постоянным периодом и амплитудой в фазовом пространстве соответствует замкнутая кривая. Аттрактор в этом случае называется устойчивым предельным циклом. Физически это означает, что при отклонении от таких колебаний система спустя некоторое время вновь возвращается к ним. Один из первых примеров детерминированного хаоса в диссипативных системах продемонстрировал американский метеоролог Эдвард Лоренц в 1963 году. Динамические системы по энергетическому признаку делятся на консервативные (характеризующиеся неизменным во времени запасом энергии) и неконсервативные (с изменяющимся во времени запасом энергии). Лоренц предложил простейшую модель конвекции воздуха (она играет важную роль в динамике атмосферы). В основе этой модели лежат представления о связи потоков воздуха в атмосфере с разностью температур ее различных слоев Непредсказуемость поведения сложных нелинейных динамических систем на больших временах обусловлена их высокой чувствительностью к начальным данным. Малые изменения начальных условий ведут к расходимости фазовых траекторий. Таким образом, в детерминированных системах с динамическим хаосом, где будущее однозначно определяется прошлым, существует конечный горизонт прогноза. По определению Германа Хакена: «Самоорганизация—это процесс упорядочения (пространственного, временного или пространственно‐временного) в открытой системе, за счёт согласованного взаимодействия множества элементов её составляющих» Использование идей и методов синергетики имеет большое значение для развития почвоведения, так как почвообразование в широком смысле является синергетическим процессом самоорганизации почвенной системы in situ в течение ее функционирования во времени и пространстве. Почвы относятся к диссипативным системам. Диссипативными называются системы, в которых энергия со временем уменьшается. Для их непрерывного функционирования необходимы источники энергии.
Костычев(1889)-1е уравнение минерализации орг вещества, Тюрин(1937)-мат выражение для предельного уровня накопления орг вещества в почве. Модель Йени(30е-40е): N-содержание азоты в почве,a-ежегодное поступление азота с раст остатками,K-константа минерализации ( доля азота, которая минерализуется в год), dN/dt=a-KN. В любое t, N(t)=Ne+(Ne-N0)*𝑒−𝑘𝑡, где Ne-стационарное содержание. dN/dt=0 (тк стационарное состояние), следовательно a-KN=0, а значит Ne=a/K. Сейчас существует около 250 моделей. Которые приведены в несколько классификаций. Классификация Дженкинсона(1990):1. компронтментальные модели: орг вещество=конечное число пулов, каждый пул трансформируется со своей скоростью, бывают однокомпронтментальные, двук., многок. 2. Некомпронтментальные модели: не дискретное количество пулов, а их спектр, орг вещество почвы-непрерывная функция качества, у неразлорженного орг вещества макс качество=1, затем качество снижается до 0. Классификация Кейса Паустина(1994): 1. Процесс-ориентированные модели-основное внимание на процессы трансформации, роль организмов выражается в неявной форме, в виде коэффициентов разложения.2. Организм-ориентированные модели: деструкторы включены в модель в явном виде, это модели пищевых цепей. Классификация Монзони, Парпарата(2009) 1.Модели микробиологические, ризосферные, внутрипочвенных агрегатов 2.Модели разложения опада, подстилки 3.Почвенные: трансформации орг вещества в почве, но без описания взаимодействия почв и растений 4. Экосистемные-рассматривают все взаимодействия 5.Глобальные-описывают биосферный цикл С. Основная проблема-гетерогенность орг вещества. Пути решения проблемы: 1. Бассате,Эгрен: рассматривается непрерывный спектр качества субстрата, V разложения-непрерывная функция качества. 2. Органическое вещество=конечное количество пулов, каждый пул-своя скорость и позиция в структуре модели, максимально распространен такой подход, 3 модуля: раст ост, деструкторы, орг вещество почв.
Ротамстедская модель RothC. Роттандстендская модель: модуль раст остатков= стойкие раст ост и легкоразлагаемые, учитывает влажность, температуру и гран состав, широко распространена, лучше всего подходит для описывания пахотных почв. Ротамстедскую модель (Roth – C), которая была разработана и параметризована на Ротамстедской опытной станции (Англия) и в настоящее время широко используется для прогнозирования изменений содержания органического углерода на различных типах почв и видов землепользований, включающих пахотные земли, пастбища и лес. Модель работает с месячным шагом, рассчитывая запас общего углерода почвы в т/га во временном диапазоне от одного года до столетия. Roth-C учитывает количество осадков (мм), температуру воздуха (°С), испарение с открытой водной поверхности (мм), поступление органического углерода в почву с растительными остатками и навозом (т/га С), процентное содержание фракции глины (0,002мм) (используется для расчета доступной растениям влаги в верхнем слое почвы и минерализации органического вещества). Модель Century Пул растительных остатков: поверхностные опад, корневой опад, устойчивый (структурный) и лабильный(метаболитический) пулы (по соотношению лигнина к N), также в модель входит лигнин и целюлоза. Учитывает также температуру, влажность и гран состав, учитывает медленные пул, пассивный пул и выщелачивание. Century – общая компьютерная модель почвенно-растительной экосистем, которая может моделировать динамики лугов, лесов, урожай и саванны. Модель моделирует динамику органического в-ва почв в природных и обрабатываемых системах и объясняет динамику С, N,P,S в почвенно-растительных системах, используя временной шаг в один месяц. Есть так же подмодель расчета содержания влаги в почве, растительная подмодель. Примеры взаимодействия подмоделей: отношение С:N, С:S, C:P влияет на продукцию растительного сообщества, при уменьшении отношения ниже заданного – происходит снижение. Содержание азота в почве так же, например, учитывает выпадение осадков и поступление с ними азота. Азот прикрепляется к углероду, теряемому в процессе дыхания. Потеря азота вместе с урожаем. Активность микробной биомассы, зависит от отношения С:Р.
Организм-ориентированные модели: деструкторы включены в модель в явном виде, это модели пищевых цепей. Классификация Монзони, Парпарата(2009) 1.Модели микробиологические, ризосферные, внутрипочвенных агрегатов ^ 2.Модели разложения опада, подстилки 3.Почвенные: трансформации орг вещества в почве, но без описания взаимодействия почв и растений 4. Экосистемные-рассматривают все взаимодействия 5.Глобальные-описывают биосферный цикл С.
Основная причина неопределенности модельных предсказаний-неоднородность объекта. Ошибки: 1. При определении структуры модели 2. При выборе сценари: при выборе использования модели –лес вместо агро(+ ошибки из за масштаба- регион вместо точки и тп) 3. Ошибки неточного определения параметров. Пример ошибок связанных с С: 1. Гумусовые пулы не соответствуют фракциям 2. Неопределенность в определении структуры модели 4.не всегда нелинейные связи почва-организмы отображаются в модели 5. Выбор сценария, масштабов 6. Неточная оценка параметров. Использование моделей динамики С: изучение отклика почв и экосистем на изменение хозяйственного воздействия и смену характера землепользования в различных регионах мира, использование при исследовании о оценке почвенного потенциала для секвистрации С, это эффективный метод исследования и проверки гипотез при изучении орг вещества почв. Важное направление развития динамики С: устойчивость связей между моделями и изменяемыми фракциями, постановка экспериментов по изучению механизмов стабилизации орг вещества почвы, изучение нелинейных связей.
Факторные модели Они основаны на концептуальной модели, которая была очень четко сформулирована В.В. Докучаевым в работе «Главные моменты в истории оценок земель Европейской России, с классификацией русских почв», опубликованной в 1886 оду в «Материалах к оценке земель Нижегородской губернии». Цитата из этой работы приведена в первой главе. В 1899 в докладе Закавказскому статистическому комитету В.В. Докучаев впервые представил свою модель в символьной форме: П = f(К,О,Г) В, где П – почва; К – климат; О – организмы; Г – материнская порода; В – возраст почвы. В этом выражении почему‐то пропущен рельеф, хотя в тексте доклада отмечается важность этого фактора почвообразования. Ч. Шоу в 1930 году S M C V D = ( ) + + T , (5.2) где S – почва, которая формируется из породы (М) под действием климата (С) и вегетации (V) во времени (Т). D – эрозия и осадконакопление. С.А. Вилде Wilde (1941; 1946) представил почвообразование в виде интеграла следующего вида: S=∫(g.e.b)dt где S – почва; g – геологическая почвообразующая порода; e –влияние окружающей среды; b – биологическая активность; t –время. Уравнение Г.С. Йенни (Jenny, 1941) s = f (cl, o, r, p ,t,…) где cl – климат; о – организмы; r – рельеф; p – почвообразующие породы; t – время. Точки указывают на возможность включения дополнительных переменных. Йенни подчеркнул разницу понятия «факторы почвообразования» по В.В. Докучаеву, с почвообразующими факторами в выражении. В этом выражении они представляют собой не движущие силы почвообразования, а только переменные, определяющие состояние почвенной системы. При создании цифровых почвенных карт успешно используется модель «SCORPAN» (McBratney et al, 2003). S=f(s,c,o,r,p,a,n) Sc – почвенная таксономическая единица; Sa – количественная характеристика почвенного свойства; s – другие свойства почвы; c– локальные климатические характеристики; o – организмы, растительность, фауна, человек; r – рельеф; p – почвообразующая порода; a – возраст, n – пространственное положение. 2.Эволюционные модели. Эволюционные модели используются в целях изучения временных трендов в развитии почв.Начнем знакомство с ними с широко известной модели Джонсона с соавт. (Johnson, Watson‐ Stegner, 1987; Johnson et al., 1990). Эта модель отражает представления о почвообразовании, как о совокупности разнонаправленных процессов одновременно протекающих в почве. Прогрес‐ сивный педогенез включает процессы, которые направлены на развитие и дифференциацию профиля. Он подразумевает увеличение мощности профиля и лучшую выраженность генетических горизонтов. Регрессивный педогенез представляют процессы, приводящие к уменьшению мощности и гомогенизации профиля. В зависимости от условий один и тот же процесс может увеличивать или уменьшать анизотропность профиля. С течением времени в почве могут доминировать те или другие процессы. Если доминируют прогрессивные процессы, то увеличивается мощность профиля и выраженность границ между горизонтами. При доминировании регрессивных процессов профиль укорачивается, а его анизотропность снижается. Изменение состояния почвы в ландшафте во времени не является однонаправленным. Монотонные тренды в развитии почв могут наблюдаться только при длительном доминировании прогрессивного или регрессивного педогенеза. В символьной форме модель была представлена следующим выражением: S = f (P, R), где S – почва или свойства почвы, P – прогрессивный педогенез и R – регрессивный педогенез. Джонатан Филлипс (Phillips, 1993) предложил модель для исследования временных трендов развития почвы в зависимости от различных комбинаций прогрессивного и регрессивного направ‐ лений. В этой модели под развитием почвы понимается увеличение мощности профиля и степени преобразования почвообразующей породы. Почвенное развитие (S) увеличивается в результате прогрессивного (Р) педогенеза и уменьшается под действием регрессивного (R). Из этого следует, что скорость почвенного развития определяется разностью скоростей прогрессивного и рег‐ рессивного педогенеза:
В
модели учтена обратная связь между
скоростью прогрессивного педогенеза
и развитием почвы S. Скорость
прогрессивного развития педогенеза
уменьшается с увеличением S в результате
истощения выветривающихся минералов
и снижения
скорости выветривания с
ростом глубины профиля. Для описания
этой зависимости выбрана экспоненциальная
функция:
3 Процессные модели Концептуальную основу математических процессных моделей педогенеза представляет модель Роя Симонсона (Simonson, 1959). Схематически она представлена на рис. I.5.3.
Известные процессные модели педогенеза условно можно разделить на две группы. Первую представляют ландшафтные модели, развитые в геоморфологии. Ландшафтные модели отражают преобразование и перемещение только твердой фазы почвы и не описывают явно циркуляцию воды и растворенных веществ в почве. Модели второй группы сосредоточены на описании образования и развития почвенного профиля. Назовем их профильными. В этих моделях в явной форме описаны потоки воды и растворенных веществ в почве.
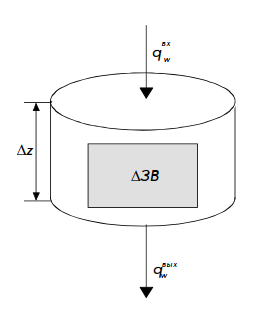
1) Процессные модели педогенеза, рассматривающие изменения только твердой фазы почвы представлены ландшафтными моделями, развитыми в геоморфологии. Ландшафтные модели В качестве примера ландшафтной модели мы выбрали простейший вариант модели почвообразования и развития ландшафта (Minasny, McBratney, 1999). В этой модели рассматривается ландшафт с высотой поверхности z почвенным слоем мощностью h и границей раздела почва – порода e вдоль горизонтальной оси x (рис. I.5.4). Предполагается, что скорость почвообразования зависит от скорости выветривания подстилающей породы в результате физических, химических и биологических процессов, за счет чего опускается граница раздела почва – порода. Изменение мощности почвенной толщи = выветривание + (привнос – вынос) вещества в результате эрозии.
Уравнение неразрывности, выражающее закон сохранения в математической форме, в этом случае имеет вид:
где h – мощность почвенного слоя; (∂e/∂t) – скорость выветривания; qs – поток вещества; ρs – плотность почвы; ρr – плотность породы; Предполагается, что скорость физического выветривания (∂e/∂t) экспоненциально убывает с увеличением мощности почвенной толщи (h)
где P0 – потенциальная (или максимальная) скорость выветривания породы, а k1 – эмпирический коэффициент. Уменьшение скорости выветривания с увеличением мощности почвы связано с экспоненциальным снижением амплитуды колебаний температуры с глубиной, а также с просачиванием воды в почву и процессами ее замораживания и оттаивания. Параметры P0 и k1 определяются климатом и свойствами почвообразующей породы. Значения P0 варьируют 0.08 до 2.0 мм в год в Северной Калифорнии и от 0.05 до 0.14 мм в год в юго‐восточной Австралии. Средние значения параметра k1 составляют 2‐4 мм в год. Перемещение вещества в ландшафте обычно рассматривается диффузионным. В этом случае поток вещества определяется следующим образом:
где qs – поток вещества, которое перемещается по склону через единицу площади в единицу времени; D – эрозионная диффузия. Она зависит от физических свойств почвы, характера растительного покрова и погоды. Подставляя (5.14) в уравнение неразрывности (5.12) и полагая, что D и ρs не изменяются в пространстве, получим уравнение почвообразования:
где ρs плотность почвы, ρr плотность породы. Таким образом, скорость почвообразования – изменение мощности почвенной толщи в единицу времени зависит от скорости выветривания и перемещения почвы в результате эрозии, которая определяется эрозионной диффузией (D) и кривизной склона. Исследование модели свидетельствует о высокой чувствительности к начальным условиям, свойственной нелинейной системам. Как обсуждалось в третьей главе, нелинейные системы характеризуется сложной и многообразной динамикой. В их поведении возможно обнаружение детерминированного хаоса – режима с очень изменчивой амплитудой. Хаотическое поведение обусловлено тем, что небольшие отклонения от начальных условий в нелинейных системах со временем могут увеличиваться, в результате чего первоначально близкие траектории будут расходиться. В дальнейшем обсуждаемая модель была усовершенствована за счет перехода от одномерного (1D) к двумерному (2D) варианту и включения описания химического выветривания, приводящего к уменьшению мощности почвенной толщи в результате растворения минералов и выщелачивания растворенного вещества (Minasny, McBratney, 2001). Важным шагом в развитии модели явилось описание обратной связи, характеризующей снижение эрозии почвы при увеличении продуктивности растительного покрова. С этой целью в модель введен индекс продуктивности – функция, изменяющаяся от 0 до 1 в зависимости от мощности почвы (Minasny, McBratney, 2006).
В моделях развития ландшафта почва представлена одним слоем, мощность которого изменяется на протяжении десятков и сотен тысяч лет. Сальвадор‐Бланес с соавт. (Salvador‐Blanes et al., 2007) попытались построить модель почвообразования в масштабе почвенного профиля, подходящую для включения в модель развития ландшафта (Minasny, McBratney, 2001). Она включает физическое выветривание грубой и тонкой фракций почвы, химическое выветривание тонкой фракции, процессы деформации и биотурбации и описывает, как со временем в результате развития почвы изменяется внутрипрофильное распределение ее плотности, содержания грубой и тонкой фракций и минералогического состава. Обсуждаемая модель имитирует образование почвенных горизонтов в результате только физико‐химического выветривания, процессов деформации и биотурбации и не описывает процессы переноса вещества, обусловленные циркуляцией воды в почве и играющие важную роль в дифференциации профиля. Тем не менее, она играет важную роль в развитии ландшафтных моделей, так как это первый шаг в направлении перехода к моделям, описывающим изменение во времени не только мощности почвенного профиля, но и образование горизонтов.
Почва=функция факторов почвообразования (Докучаев).Почвенные модели: 1.основаны на описании изменений тв фазы и в явном виде не описывают циркуляцию воды и почвенных растворов. 2 группы моделей: а. Основаны на линейном тренде. Представляются в виде троичных диаграмм, это простейшие модели которые не рассматривают собственно процессы б. Модель Mincsny McBratney.Это процессная модель, определяет динамику изменения почвенного слоя, которая в своюб очередь определяется разностью скоростей 2х процессов: выветривания нижележащей породы и перемещения почвенного материала в результате эрозии. 2. Модели определяющие жидкую фазу и ее взаимодействие с тв фазой. В основе уравнение неразрывности: dm/dt=-(dI/dx)±I, где dm-масса вещества в ед обьема, а dI/dz-градиент потока, I-поток m через ед сечение в ед времени, z-вертикальная составляющая, положительным считается направление вниз. Вертикальная миграция растворенных веществ: d(Qc)/dt=d/dz*[D*{d(Qc)/dz}-q*c±I], где Q-обьемная влажность, c- концентрация вещества в растворе, q-поток влаги в почве, q*c-поток за счет силы гравитации, D*-коэффициент гидродинамической диффузии.а. Модель идеального подзола (УИП 5). Допущения: гомогенная, рыхлая порода (песок), состоит из 2х частей: устойчивой (кварц) и растворимой, есть органическая часть растворяющая породу(фульва), продукты растворения биофилы, биофилы выносятся, кварц остается. Суть модели в написании уравнений для каждой составляющей: воды, фульвы, вещества, биофилов, кварца. В итоге имеем 5 процессов элл. В подзоле, чтобы решить уравнения необходимо задать начальные ( порода и биофилы от 0 до z) и граничные условия( поверхность почвы-до глубины расчетов).Эта модель исследует динамику фронта иллювиирования (зоны перехода, ниже которой разрушено <30% мат породы, а выше сохранилось неразрушенным >30%). Но есть ряд вопросов: стационарен ли фронт и если есть некий предел мощности, то чем она определяется, от чего зависит и тп. Модель подзолообразования Orthod Имеет модульную структуру. Упрощения: почва на песке, бореальные леса северной америки, нет заболачивания. Модуль влагопереноса, миграции веществ, теплопереноса, растворения минералов, разложения орг части, ионного обмена, осадков и их хим состава. Разные временные шаги: у модулей влагопереноса и ионного обмена 0,1 сутки, у всех остальных=1 сутки). Модель отвечает на вопросы: сколько поступает в почву орг вещества при разложении подстилки, какие механизмы ответственны за накопление элементов в В горизонте, что выносится из профиля и тп. CALGIP -Модель формирования Са и гипсового горизонта в аридных почвах, имеет модульную природу. Модуль осадков стохастический ( то есть на выходе имеем не четкие значения, а их вероятностный диапозон). Подмодели: миграция Са и сульфат ионов, массообмен Са и сульфат ионов между жидкой и тв фазами, ионообмен с ППК, растворение гипса и кальцита, динамика СО2 в газовой фазе, взаимодействие жидкой и тв фазы по закону Генри. Шаг по времени=1 сутки. Переменные: количество осадков, поступление с ними Са и сульфат ионов, поступление Са и сульфат ионов с пылью, плотность почвы, полевая влагоемкость, влагозавядание. Рассматривает вопросы: как сульфат ион меняет миграционную способность Са, на какой глубине формируются соответсвующие горизонты. Обратная задача: знаем глубину горизонтов и вычисляем условия формирования, входные функции и параметры. SOILGEN - имитационная модель для изчения мат породы. В то время как генетич исслед почвы реконстуируют исходную мат породу, эта моель реонструирует с помощью начальных условий почвообразования мат породу, беря за основу определение почвы как "функции факторов почвообразования"
Параметр – это числовой коэффициент или свободный член уравнения, полученный операцией подбора (аппроксимацией) выбранной функцией экспериментальных данных. Аппроксимация по методу наименьших квадратов – операция подбора параметров выбранной функции для экспериментальных данных, основанная на нахождении минимума среднеквадратической ошибки экспериментальных данных. Критерий получения параметров нам известен, это нахождение минимума среднеквадратической ошибки
В данном случае можно представить среднеквадратическую ошибку в следующем виде (для упрощения расчета возьмем четыре пары значений):
Решением данного уравнения будут конкретные численные значения для параметров b1 и b2. Данное уравнение не удастся решить обычным способом – два неизвестных в одном уравнении. Необходимо использовать другие методы. Для нахождения значений параметров в многопараметрических нелинейных уравнениях используют алгоритмы решения вычислительных задач методами высшей математике, которые можно разделить на детерминистические и стохастические. Давайте разберем наиболее показательный детерминистический метод сканирования или симплекс‐метод. Прежде всего, представим поле параметров b1 и b2 в виде крупной сетки (рис. II.3.19). В узлах сетки рассчитывается значение Sr. Начнем, например, со значения b2=0.3 и b1=0.3 (точка А). Тогда можно рассчитать Sr в этой точке:
Казалось бы, что на всем поле значений b1 и b2 значение 0.28 и является минимальным, так как в других узлах значения выше, а нам ведь надо найти минимум среднеквадратичной ошибки. Однако, если «измельчить» сетку, рассчитать значения параметров в ближайших точках, то можно найти такую точку, вокруг которой все значения на рассматриваемом поле параметров будут увеличиваться. Достигнут минимум Sr в рассматриваемом поле параметров. Для точки достигнутого минимума мы и определяем b1 и b2. В данном случае они равны b1= 0.628 и b2 =0.401. Таким образом, искомое уравнение после операции сканирования приобрело конкретный вид:
СТАТИСТИКИ ДЛЯ АНАЛИЗА ПАРАМЕТРОВ
Случайные погрешности не имеют преимущественного направления (в сторону плюса или минуса) и уравновешивают друг друга. Эти погрешности возникают в результате случайных отклонений значений изучаемого показателя в исследуемой выборке (ошибка экспериментатора, единичные случаи изменения внешних условий и др.). Эти отклонения объясняет теория вероятности. В отличие от случайных отклонений систематические погрешности направлены в сторону только преувеличения или только преуменьшения в результате действия на изучаемую систему неучтенного фактора (рис. II.3.15). Таким фактором, как правило, бывает методическая неточность (смещение нуля шкалы прибора, шкала нанесена неравномерно; капилляр термометра в разных участках имеет разное сечение и др.), что нередко приводит к заметным ошибкам и, более того, к неверной интерпретации процессов. Поэтому анализ появления случайных ошибок – чрезвычайно важный этап регрессионного анализа.
се множество функций, применимых к описанию явлений в природе, можно разделить на несколько больших групп в зависимости от направленности процесса: I. Монотонные 1. Возрастающие 2. Убывающие II. С одним экстремумом III. С несколькими экстремумами IV. С изломом Монотонные
(убывающие и возрастающие) функции
Все
множество убывающих и возрастающих
функций можно разделить на пять
типов:
1. Линейная y=b1+b2x
2.
Степенная (за исключением параболы)
Функции
с одним экстремумом
Среди
функций, имеющих один максимум или
минимум
можно выделить две, часто
используемые в естественных науках:
1.
Параболическая
Функции с несколькими экстремумами 1.
Полиномы 3‐й
и более высокой степени
I.Убывающие: 1.бином b1(1-x/b2); 2.степенная (x/b2)-b1; 3.Экспоненциальная b1exp(-x/b2); 4.Логистическая b1/(1-(b2/x)-b3); b1x/(x-b2); II.Возрастающие (те же, что и убывающие, только с другими коэффициентами); III.С одним максимумом: 1.Параболические b1-(x/b2)b3; .2.Гауссиана b1exp(-(x-b2)2/b3); IV.С одним минимумом (те же, что и с одним максимумом, но только с другими коэффициентами); V.С несколькими экстремумами (например, сплайн-функция или сумма 2-х гауссиан); VI. С изломом (все функции, в которых есть модуль, например, y=|x| или y=|sinx|) из того, что встречается в природе – транспирационная трапеция; Михаэлиса-Ментен (dS/dt=V0S/(Km+S), Km – константа Михаэлиса – концентрация, при которой достигается ½max скорости).
1. Для каждого почвенного слоя необходимо экспериментально определить основную гидрофизическую характеристику в виде дифференциальной влагоемкости С(θ, Рк‐с). 2. Для каждого почвенного слоя необходимо знать и функцию влагопроводности Квл(Рк‐с). Возникает вопрос: как найти величину Квл (Рк‐с) между двумя соседними слоями? Применяют несколько способов: (1) усредняют саму величину влагопроводности, (2) усредняют сначала влажность слоев, а затем находят влагопроводность для усредненной влажности и (3) усреднение с учетом толщины слоя почвы. Считается, что последний метод дает лучшие результаты. 3. Задается конкретная глубина почвы и указывается срок, для которого надо производить расчет. Действительно, это необходимо для того, чтобы свести баланс. Глубина почвы указывается в виде верхней (обычно поверхность почвы) и нижней границ. 4. Необходимо задать и условия на нижней границе, иначе невозможно свести баланс. Обычно это либо: – постоянная влажность или давление влаги на нижней границе (условие 1‐го рода). Его используют, например, при наличии грунтовых вод в нижней части профиля; – свободный сток или постоянный градиент давления (условие 2‐го рода). Граничное условие характерно для автоморфных почв с глубоким уровнем грунтовых вод; – поток через нижнюю границу пропорционален градиенту движущей силы и коэффициенту проводимости (обобщенное граничное условие 3‐го рода). Это условие обычно используют при наличии на нижней границе плохо проницаемого слоя, в случае поступления грунтовых вод через этот слой. 5. Необходимо задать условия и на верхней границе, иначе невозможно свести баланс. Это условие формулируется в виде приходных и расходных статей: осадки, поливы, испарения и транспирация. В большинстве случаев это величины ежесуточных (декадных и пр.) экспериментальных данных. Для больших территорий и агроценозов эвапотранспирацию можно рассчитать на основе стандартных метеоданных. Начнем с ввода почвенных гидрофизических данных – пункт 1 и 2. Имеем собственно почвенно‐гидрофические данные для каждого слоя в виде основной гидрофизической характеристики и функции влагопроводности. Вспомним, что основная гидрофизическая характеристика (ОГХ) – это зависимость объемной влажности почвы (см3/см3 или безразмерная величина) от капиллярно- сорбционного давления влаги (см водного столба или другие единицы давления. Часто используется внесистемная единица pF, равная десятичному логарифму модуля давления влаги в см водного столба, величина, аналогичная pH в химии). Экспериментальное определение ОГХ, θ(h) – это отдельная область физики
Примеры условий для моделей влагопереноса.
Вспомним, что основная гидрофизическая характеристика (ОГХ) – это зависимость объемной влажности почвы (см3/см3 или безразмерная величина) от капиллярно‐сорбционного давления влаги (см водного столба или другие единицы давления. Часто используется внесистемная единица pF, равная десятичному логарифму модуля давления влаги в см водного столба, величина, аналогичная pH в химии). В процессе работы программы функцию (ОГХ) надо вводить не в виде экспериментальных точек (пар значений функция–аргумент), а в виде функциональной зависимости, которая статистически наиболее точно описывает экспериментальные данные. Аналогично все происходит и с функцией влагопроводности, K(h). Учитывая важность и значение, которое имеет ОГХ в гидротермических почвенных моделях, остановимся на основных и наиболее используемых в настоящее время (более подробно см. Глобус А.М. 1987). Во‐первых, в большинстве подходов используют приведенное, или относительное значение влажности почв,
где θi – текущая влажность, соответствующая капиллярно‐сорбционному давлению влаги Рi; θs – влажность насыщения, величина влажности почвы, близкая (но, как правило, не равная) значению порозности, т.е. когда все поровое пространство заполнено водой, θr – остаточная влажность почвы. В большинстве случаев указанные влажности определяются как эмпирические параметры в процедуре аппроксимации экспериментальных данных. Во‐вторых, чтобы описать «ступеньку» быстрого выравнивания кривой ОГХ в области от насыщения до давления входа воздуха («давления барботирования»), используют величину «давление барботирования». Эта величина позволяет физически обоснованно определить точку перегиба. В современных моделях для описания ОГХ чаще всего используют две функции. Первая, степенная, была предложена Бруксом и Кори. (Brooks and Corey, 1964):
где α – эмпирический параметр, равный величине обратной давлению входа воздуха, или давлению барботирования. Вторая наиболее часто используемая функция для описания ОГХ была предложена американским физиком почв ван Генухтеном (van Genuchten, 1980):
где m=1–1/n , n >1 также является эмпирическим параметром, характеризующим крутизну наклона ОГХ. И здесь α – эмпирический параметр, равный обратной величине давления входа воздуха. Здесь указаны основные функции для описания ОГХ, используемые в большинстве современных моделей. Желающих более подробно ознакомиться, с различными математическими функциями для описания ОГХ, отсылаем к монографии А.М. Глобуса (1987). Указанные функции относятся только к ОГХ. Но в уравнение Ричардса входит еще одна функция – функция влагопроводности. Поэтому, далее теория гидрологии почв развивалась в следующем направлении. Известно, что ОГХ в дифференциальном виде представляет собой не что иное, как распределение объемов пор по их радиусам. Влагопроводность почвы также определяется распределением пор по размерам и их заполненностью водой. Поэтому, для получения функции влагопроводности K(Рк‐с) можно использовать параметры ОГХ и нормирующий фактор, а именно величину влагопроводности при полном заполнении пор почвы водой. Это не что иное, как коэффициент фильтрации или насыщенная гидравлическая проводимость Ks . Поэтому для функции влагопроводности Брукс и Кори предложили следующую зависимость
где Ks – коэффициент фильтрации для данного почвенного слоя, l – эмпирический параметр, отражающий взаимосвязанность пор почвы (для многих почв принимается значение 0.5). На основе уравнения ван Генухтена и статистическом распределении объемов пор по размерам, израильским исследователем Муалемом для описания функции влагопроводности была предложена следующая зависимость:
Так как при получении этого уравнения были использованы подходы, разработанные ван Генухтеном и Муалемом, это уравнение для функции влагопроводности носит название уравнения ван Генухтена‐Муалема. Итак, уравнения Брукса‐Кори и ван Генухтена позволяют описать экспериментальные данные ОГХ гладкими функциями, и использовать параметры аппроксимации для функции влагопроводности. Все эти процедуры (аппроксимации экспериментальных данных) выполняются либо в специальных программах расчета влагопереноса, либо в стандартных математических пакетах (STATISTICA, SIGMAPLOT и др.).
Итак, мы с вами разобрали основные составляющие моделей влаго, тепло‐ и солепереноса в почвах, уделив внимание внутрипочвенным процессам переноса, а также процессам, которые происходят на границах почвенной толщи. Эти процессы формируют основные блоки почвенных моделей переноса вещества и энергии. Отдельные блоки модели функционирования почвы во взаимосвязи с контактирующими природными телами (с приземным слоем атмосферы, растениями, грунтами и грунтовыми водами) представлены на рис.II.7.1. Для каждого блока существует свой предпроцессор, для модели на конечном послерасчетном этапе – постпроцессор. Используя ту или иную модель, мы обязательно начинаем с конкретного блока, например, «почва». И сначала используем предпроцессор этого блока. Устройство этого предпроцессора нам знакомо. Организован он в виде таблиц, в графы которых мы должны ввести параметры и свойства гидрофизических характеристик почвы. Напомним, это параметры уравнения ван Генухтена (θs, θr, λ, n), описывающие основную гидрофизическую характеристику (ОГХ), насыщенную гидравлическую проводимость (коэффициент фильтрации Кф), либо фундаментальные физические свойства, позволяющие по педотрансферным функциям рассчитывать указанные показатели. Пример такого гидрофизического предпроцессора приведен в табл. II.2.1 (глава 2). Мы вводим необходимую информацию по гидрологии почвы, начальным (начальное распределение влажности и/или давления влаги) и граничным условиям в память компьютера. Ядро программы выполняет расчет введенной модели методом конечных элементов. После расчета явлений переноса необходимые данные попадают в постпроцессор, который обеспечивает обработку результатов расчета модели и вывод их в интерактивном графическом режиме. В некоторых моделях результаты расчета могут быть реализованы в табличном виде, графическом (например, в виде хроноизоплет) или в виде анимационных построений, например, динамики влажности, давления, ионов, механических нагрузок и пр. Дело специалиста разобраться и сделать правильные целевые выводы на основании полученных данных.
В современных моделях учитывается сложность почвенной системы, взаимосвязь почвы с контактирующими природными телами и многоцелевые задачи модели. Используют так называемый «принцип платформ», который заключается в том, что создается некая платформа для размещения и взаимосвязи ряда блоков, разработанных в различных научных областях. Например, платформа VSoil основана на том принципе, что мы можем разделить различные биологические, физические и химические процессы, происходящие в почвах и для каждого из них заполнить списки входных и выходных переменных. Используя эту информацию, платформа «находит» связи между процессами и создает основу, которая будет использоваться для построения моделей. Второй принцип работы платформы заключается в том, что для любого процесса могут быть доступны несколько представлений. Обычно эти теоретические (практические) подходы называют модулями. Модули соответствуют различным подходам к моделированию (математические представления, численные решения и т.д.). Модуль использует подмножество входных и выходных величин для процесса, который должен быть описать. Следовательно, платформа содержит список процессов и переменных, который может быть расширен добавлением новых процессов и переменных. Она содержит также уже имеющиеся модули для некоторых процессов. Платформа напоминает студию для разработки и тестирования новых модулей. Пользователь платформы может создать свою собственную модель, собирая соответствующие модули. Безусловно, во время этой сборки, платформа помогает, подсказывает решения, ограждает от неверных шагов и пр. Действительно, все это, напоминает детскую игру‐сборку различных конструкций из типичных деталей – «ЛЕГО». Недаром, некоторые такие модели‐платформы и называются, например, «ECOLEGO».
Эмпирические – аппрокисмация типа регрессионные уравнения; полуэмпирические – то же но с учётом закономерностей Высокая общность этих моделей (стр-ра модели сохраняется, меняются только входные характеристики и параметры), могут быть использованы с целью проверки гипотез. Трудности: множественность разбития на блоки, число отражаемых связей м.б. разным. Степень подробности – обычно серия постепенно усложняющихся моделей. Важно помнить, что с увеличением сложности будет происходить увеличение точности, но в какой-то момент точность начнет падать, важно уловить эту точку перегиба – точку отпимума. Проверка адекватности (качественные критерии ( метод Сайерта: совпадение средней и совпадение по времени экстремумов, форма кривых, обращаем внимание на max и min, а так же поведение в этих точках; анализ остатков – разница между расчетными и экспериментальными значениями (должны быть распределены нормально, не зависеть от самой величины и не зависеть от времени); анализ коэффициента автокорреляции), количественные оценки (max относ ошибка имитации=max|Δxi/xi|; средняя относительная ошибка имитации Sr=1/N *∑ nj*∆j ; средняя квадратическая ошибка имитации=
Нормализованная обьектная функция NOF=S2имит/Y̅. Вероятн. грубой ошибки: P=100*Nаномальн/Nвсего показатель
Тейла Критерий Вильямса-Клюта. Vi=0,5(Δ1+Δ2); Ui=Δ2-Δ1; a=Vi/Ui; p<0,05 графики отличаются; t>0 первый график лучше.
Как мы уже знаем математические модели могут быть физически обоснованными и стохастическими (или статистическими), динамическими и стационарными, точечными и пространственно распределенными, аналитическими и численными (их еще называют имитационными или полуэмпирическими). Физически обоснованные – это означает, что в основе моделей лежат физические законы, как правило, такие незыблемые, как закон баланса вещества и энергии и закон переноса – законы, которые свойственны всей обозримой Вселенной. Именно это качество моделей существенно расширяет их возможности. В отличие от стохастических моде‐ лей, которые с определенной надежностью работают только в диапазоне их построения, физически обоснованные модели могут применяться в более широком диапазоне условий, воспроизведение которых весьма затруднительно или просто невозможно в природе. Например, модели каких‐либо природных или антропогенных катастроф. Безусловно, это значительно расширяет возможности использования моделей. Законы неразрывности и переноса Закон баланса в математических моделях представлен в виде так называемого уравнения неразрывности. Рассмотри его вывод на примере движения воды в почве. Пусть у нас имеется некий цилиндр почвы единичной площади и высотой ∆z, в который втекает поток влаги qwвх , а вытекает qw вых . За счет разницы этих потоков ∆q за некоторое время ∆t происходит изменение запасов влаги ∆ЗВ (рис. II.1.1).
Это соотношение потоков и изменения запасов влаги за некоторый период времени можно зависать в виде уравнения:
Учитывая, что изменение запасов влаги – это изменение объемной (Δθ) влажности в толще ∆z, запишем
Если принять, что баланс воды происходил в i‐ом слое почвы толщиной ∆z, и в него могло втекать или вытекать некоторое количество воды ( ) q q w w вх вых - за время ∆t, то уравнение баланса можно записать в более общем виде:
Обозначая разницу потоков через ∆q и при отсутствии притоков и оттоков влаги с боковой поверхности, а также появление влаги в рассматриваемой толще за счет других источников (на‐ пример, конденсации), получаем
Это и есть выражение уравнения неразрывности, полученное нами, на основе только балансовых соотношений. Из уравнения неразрывности для почвенной влаги следует, что «Изменение влажности определенной толщи почвы во времени пропорционально изменению потока влаги в ней» и записывается, если перейти от конечных разностей к частным дифференциалам как
Полученное уравнение является основным при математическом моделировании. Оно применимо не только для воды, но и для потока ионов, нерастворимых веществ, тепла и пр. Более того, используя балансовые соотношения можно строить математические прогнозные модели. Эти модели так и называются «балансовыми», они весьма простые по внутреннему устройству, не требуют большого количества почвенной информации. С ними можно познакомиться в книгах по физике почв. Итак, первое уравнение в физически обоснованных моделях – это балансовое уравнение, используемое в виде уравнения неразрывности. Второе – это уравнение переноса веществ и энергии, которое в самом общем виде выглядит так:
де q – удельный поток (или поверхностная плотность потока) вещества или энергии (размерность [г/(см2 сут)] или [кал/(см2 сут)]). К – коэффициент пропорциональности, точнее – проводимости, характеризующий переток вещества или энергии при единичном градиенте движущей силы Ψ. Вспомним
и уравнение Дарси, описывающее поток
влаги в насыщенной влагой почве
Известно, что движение воды в почве описывается законом Дарси. Для насыщенной влагой почвы этот закон записывается как:
где
qw
–
поток влаги в почве (размерность: см
водного слоя/сут), Кф
–
коэффициент фильтрации, а отношение
Функция влагопроводности – зависимость коэффициента влагопроводности (ненасыщенной гидравлической проводимости, Квл) от капиллярно‐сорбционного (Рк‐с) давления почвенной влаги или от влажности почвы (θ): Квл = f P ( , ) к‐с θ . Нередко обозначают его Квл (Рк‐с) или Квл(θ). Для нас очень важно, что функция эта нелинейная, резко уменьшающаяся при падении давления влаги в почве. Кроме того, учитывают, что перепад гравитационного давления (∂Pгр ) на расстоянии z равен этому расстоянию. Поэтому при выражении гравитационного давления в тех же единицах, что расстояние, градиент гравитационного давления равен единице, т.е.
Но поскольку за положительное направление движения влаги выбрано движение вверх, к поверхности почвы, то при движении влаги вниз, которое вызывает гравитационное давление,
И в этом случае модифицированное уравнение Дарси можно записать:
Учитывая, что поток влаги есть изменение объемной влажности ∂θ за период времени ∂t, в случае одномерного вертикального потока это уравнение записывают либо в векторном виде, либо в обычной форме
Кроме того, для переноса в вертикальном направлении, когда градиент гравитационного давления равен 1 (уточним – при одинаковых единицах измерения расстояния и давления), можно записать:
Нетрудно заметить, что в этом уравнении две переменные – влажность ( θ ) и давление влаги (Рк‐с). Решения его даже специальными методами невозможно. Надо привести уравнение к одной переменной. Для этого вводят понятие дифференциальной влагоемкости
ту величину используют, экспериментально или другими способами получая основную гидрофизическую характеристику ОГХ («кривая водоудерживания», «water retention curve») – зависимость объемной влажности почв от капиллярно‐сорбционного давления. В результате подстановки в уравнение влагопереноса дифференциальной влагоемкости, мы получаем запись основного уравнения движения влаги, которое и носит название уравнения Ричардса. Для ненасыщенной почвы уравнение Ричардса можно записать с использованием дифференциальной влагоемкости:
где ±I( , ) z t – это член «источник/сток», т.е. либо добавочное появление воды в рассматриваемом слое, либо, напротив (со знаком минус) её исчезновение. Обычно, добавочное появление влаги в почвенном слое не рассматривается, т.к. физически это не очень существенный процесс при одномерном рассмотрении, связанный, например, с конденсацией влаги. А вот исчезновение влаги (–I) вполне весомый процесс, связанный с потреблением влаги корнями растений и её расходом на транспирацию. Этому процессу будет посвящен отдельный раздел. Итак, уравнение Ричардса – это центральное, самое важное уравнение передвижения влаги, веществ и энергии в почвах. Важно также отметить, что это уравнение было получено на основе балансового уравнения (уравнения неразрывности) и уравнения переноса (модифицированное уравнение Дарси), т.е. на основе фундаментальных физических законов. Вспомним, что основная гидрофизическая характеристика (ОГХ) – это зависимость объемной влажности почвы (см3/см3 или безразмерная величина) от капиллярно‐сорбционного давления влаги (см водного столба или другие единицы давления. Часто используется внесистемная единица pF, равная десятичному логарифму модуля давления влаги в см водного столба, величина, аналогичная pH в химии). В процессе работы программы функцию (ОГХ) надо вводить не в виде экспериментальных точек (пар значений функция–аргумент), а в виде функциональной зависимости, которая статистически наиболее точно описывает экспериментальные данные. Аналогично все происходит и с функцией влагопроводности, K(h). Учитывая важность и значение, которое имеет ОГХ в гидротермических почвенных моделях, остановимся на основных и наиболее используемых в настоящее время (более подробно см. Глобус А.М. 1987). Во‐первых, в большинстве подходов используют приведенное, или относительное значение влажности почв,
где θi – текущая влажность, соответствующая капиллярно‐сорбционному давлению влаги Рi; θs – влажность насыщения, величина влажности почвы, близкая (но, как правило, не равная) значению порозности, т.е. когда все поровое пространство заполнено водой, θr – остаточная влажность почвы. В большинстве случаев указанные влажности определяются как эмпирические параметры в процедуре аппроксимации экспериментальных данных. Во‐вторых, чтобы описать «ступеньку» быстрого выравнивания кривой ОГХ в области от насыщения до давления входа воздуха («давления барботирования»), используют величину «давление барботирования». Эта величина позволяет физически обоснованно определить точку перегиба. В современных моделях для описания ОГХ чаще всего используют две функции. Первая, степенная, была предложена Бруксом и Кори. (Brooks and Corey, 1964):
где α – эмпирический параметр, равный величине обратной давлению входа воздуха, или давлению барботирования. Вторая наиболее часто используемая функция для описания ОГХ была предложена американским физиком почв ван Генухтеном (van Genuchten, 1980):
где m=1–1/n , n >1 также является эмпирическим параметром, характеризующим крутизну наклона ОГХ. И здесь α – эмпирический параметр, равный обратной величине давления входа воздуха. Здесь указаны основные функции для описания ОГХ, используемые в большинстве современных моделей. Желающих более подробно ознакомиться, с различными математическими функциями для описания ОГХ, отсылаем к монографии А.М. Глобуса (1987). Указанные функции относятся только к ОГХ. Но в уравнение Ричардса входит еще одна функция – функция влагопроводности. Поэтому, далее теория гидрологии почв развивалась в следующем направлении. Известно, что ОГХ в дифференциальном виде представляет собой не что иное, как распределение объемов пор по их радиусам. Влагопроводность почвы также определяется распределением пор по размерам и их заполненностью водой. Поэтому, для получения функции влагопроводности K(Рк‐с) можно использовать параметры ОГХ и нормирующий фактор, а именно величину влагопроводности при полном заполнении пор почвы водой. Это не что иное, как коэффициент фильтрации или насыщенная гидравлическая проводимость Ks . Поэтому для функции влагопроводности Брукс и Кори предложили следующую зависимость
где Ks – коэффициент фильтрации для данного почвенного слоя, l – эмпирический параметр, отражающий взаимосвязанность пор почвы (для многих почв принимается значение 0.5). На основе уравнения ван Генухтена и статистическом распределении объемов пор по размерам, израильским исследователем Муалемом для описания функции влагопроводности была предложена следующая зависимость:
Так как при получении этого уравнения были использованы подходы, разработанные ван Генухтеном и Муалемом, это уравнение для функции влагопроводности носит название уравнения ван Генухтена‐Муалема. Итак, уравнения Брукса‐Кори и ван Генухтена позволяют описать экспериментальные данные ОГХ гладкими функциями, и использовать параметры аппроксимации для функции влагопроводности. Все эти процедуры (аппроксимации экспериментальных данных) выполняются либо в специальных программах расчета влагопереноса, либо в стандартных математических пакетах (STATISTICA, SIGMAPLOT и др.). Весьма важным в уравнении Ричардса является то, что в его левой части стоит член изменения влажности во времени, т.е. уравнение обладает явной предсказательной силой. Если его удастся решить, то можно предсказать, какова влажность в следующий момент времени и можно прогнозировать изменение влажности в конкретном слое почвы в определенный промежуток времени. Какими же способами решают это уравнение? Для этого надо перейти к конечно‐разностной форме уравнения Ричардса:
Педотрансферные функции - это функциональные соотношения, которые переводят доступные почвенные свойства (например, текстура, структура, содержание органическое углерода и др.) в недостающие (например, почвенно-гидрологические характеристики). ОГХ, функция влагопроводности и параметры, определяющие форму и положения кривых гидрофизических функций, существенно зависят от таких фундаментальных свойств почв, как гранулометрический состав, содержание органического вещества, плотности почв и др. Существует два основных метода определения педотрансферных функций. 1‐й способ – точечный. Этот метод основан на том, что некая точка на ОГХ соответствует определенному давлению конкретной влажности. Например, надо найти влажность θi при i‐том давлении влаги. Имея достаточный набор экспериментальных данных, который обязательно включает гранулометрический состав (например, в виде содержания физического песка, пыли, и ила, содержание органического вещества С, плотность почвы bρ, можно с помощью методов множественной регрессии найти эмпирические регрессионные коэффициенты a, b, c, d, e, f. Затем для конкретного образца с помощью полученной регрессионной зависимости можно найти, влажность для данного i‐го давления влаги. 2‐й способ – параметрический. В этом способе методами множественно регрессии или какими‐либо другими определяют зависимости параметров ОГХ (α, n, θr и θs) от фундаментальных физических свойств. Этот метод быстрее и удобней, но менее точен. Таким образом, для того, чтобы получить и использовать педотрансферные функции, необходимо: 1. Иметь большую базу данных по ОГХ и базовым свойствам различных почв. Последние работы показали, что педотрансферные функции лучше создавать для конкретного региона на своей региональной базе научных данных, для повышения точности. 2. Выбрать способ получения педотрансферных функций. Это могут быть множественная регрессия, статистические методы, использующие нейронные алгоритмы, и многие другие. 3. Надо иметь в виду, что современные модели переноса веществ снабжены ориентированными базами данных и «зашитыми» внутри модели педотрансферными функциями. Поэтому, когда в меню модели, отражающем почвенный блок, просят ввести данные по гранулометрическому составу, плотности почв и т.д., это означает, что используются ранее полученные и «зашитые» педотрансферные функции. Но необходимо обязательно уточнить, для каких почв получены эти педотрансферные функции, какая использовалась база данных, какой математический способ восстановления применяется. Эти особенности получения педотрансферных функций, «зашитые» в модели, может иногда привести к серьезным ошибкам в ваших расчетах. Только соблюдая эти правила, можно относиться к педотрансферным функциям, как к «волшебной палочке-выручалочке»: «Педотрансферные функции превращают данные, которые у нас есть, в данные, которые нам нужны!»
1) Явление перемещения вещества в пористом пространстве в результате действия механизмов механической и молекулярной диффузии получило название гидродинамической дисперсии, перенос растворенных веществ в почве называют конвективно‐дисперсионным, а уравнение его описывающее – уравнением конвективно‐диффузионного переноса (КДП):
2.1)
Процессы
ионного обмена.
В химии их классифицируют как
«гомогенный» и «гетерогенный».
Гомогенный
ионный обмен происходит в водной среде
в отсутствии активной твердофазной
поверхности
(поверхности обмена). Для применения к гомогенному ионному обмену количественных подходов используются методы термодинамики равновесных процессов. Зная константы равновесия и активности ионов в растворах, можно использовать термодинамические уравнения равновесия. На этом принципе построены модели расчета различных почвенных реакций, таких как диссоциация угольной кислоты, диссоциация бикарбонат иона, диссоциации воды и т.д., что позволяет рассчитывать карбонатно‐кальциевые равновесия в почвах, а также процессы осаждения/растворения твердой фазы (растворение гипса, кальцита, гидрооксида железа и пр.).
2.2) Если в растворе присутствует ионообменник, например, почвенный коллоидный комплекс, это значительно осложняет ситуацию. Классические методы, основанные на гипотезе об однородности обмена, в этом случае не работают (гетерогенный обмен). Поэтому в химии почв при моделировании и расчетах катион‐обменных реакций используют не термодинамические уравнения, а полуэмпирические модели селективного обмена. Принимается, что активность соединения «катион‐обменная позиция» пропорциональна его доле в суммарном заряде обменных катионов. В российской школе химии почв катион‐обменные реакции обычно рассчитывают по Гапону (известный физико‐химик, работавший в Тимирязевской академии, оставивший весьма заметный след работами по изучению обменных реакций в почве), либо по Венслоу, реже по Никольскому. Следует отметить, что большинство современных моделей для описания обменных процессов используют именно подход Гапона. 3)
Сорбция.
Движущееся
вещество может исчезать из раствора
не только вследствие его распада.
Вещество может сорбироваться твердой
фазой почвы. Если происходит сорбция
вещества, то в уравнение переноса
мигранта, следует ввести его концентрацию
в адсорбированной фазе (Сs,
моль/г), т.е. количество молей вещества,
приходящееся на грамм твердой фазы.
Тогда основное уравнение переноса
(конвективно‐диффузионное)
будет выглядеть следующим образом:
3.1) Мгновенная. Физически – чем выше концентрация вещества в растворе, тем больше его сорбция. Математически это процесс выражается в виде ряда уравнений. Если время ионообмена между твердой и жидкой фазами почвы пренебрежимо мало по сравнению со временем прохождения потока влаги через почвенный слой, для простых ионов используют уравнение линейной равновесной сорбции: Cs=k0*c, где k0 – константа сорбции или коэффициент распределения вещества между жидкой и твердой фазами почвы, а с – концентрация вещества в растворе [моль/л]. Более сложные взаимодействия, например, адсорбцию тяжелых металлов или пестицидов, описывают изотермой Лэнгмюра или Фрейндлиха. В случае длительного протекания химического реакций или процессов трансформации вещества пользуются кинетическими уравнениями разного порядка. Экспоненту Фрейндлиха можно рассматривать как показатель неоднородности сорбционных центров. Она приближается к нулю по мере возрастания неоднородности и стремится к единице при увеличении их однородности. Нередко в современных моделях переноса сложных веществ (например, пестицидов) обычное степенное уравнение Фрейндлиха записывают с использованием референтной концентрации: Xeq=KF*Cl,r*(Cl/Cl,r)N, где Xeq - содержание передвигающегося в почве вещества в сорбированном виде [кг/кг]; KF - коэффициент Фрейндлиха для процессов сорбции [м3/кг]; Cl,r - референтная концентрация в жидкой фазе [кг/м3]; Cl - концентрация вещества в жидкой фазе почвы [кг/м3]; N - экспонента Фрейндлиха. 3.2) С двумя центрами. Идея подхода заключается в том, что вместо того, чтобы разбивать поровое пространство на проводящую (межагрегатную) и застойную (внутриагрегатную) зону, вводят два механизма сорбции – мгновенную и кинетическую. Физическим оправданием является наличие в почве разных минералов, органического вещества, оксидов алюминия и железа и пр., которые избирательно и с разной интенсивностью взаимодействуют с переносимыми химическими веществами. Для упрощения модели предлагается разделить все типы взаимодействия на два: 1. Мгновенное, описываемое уравнением линейной равновесной сорбции; 2. Кинетическое, с линейной изотермой сорбции 1‐го порядка. Подход для описания сложного процесса сорбции во многом формальный, никто не знает методов определения числа (концентрации) центров мгновенного (равновесного) и кинетического (динамического) равновесия, однако, этот подход применяется повсеместно в разных моделях. Для описания динамической сорбции используют уравнение кинетики 1‐го порядка (функция экспоненциально убывающая). Также считается, что сорбция на сорбционных центрах 1‐го типа происходит мгновенно (в уравнении нет параметра времени), это сорбция всегда равновесный процесс. На центрах 2‐го типа, которые сорбируют по кинетике 1‐го порядка, происходит неравновесная динамическая сорбция. 4) Разложение. Если вещество распадается (разлагается по линейному закону), то, описание этого процесса следует вести по кинетике реакции нулевого порядка. Физически этот процесс описывается линейной убывающей функцией, Ci= C0 –k0t, где С0 – начальная концентрация в начальный (нулевой) момент времени, k0 – константа кинетики нулевого порядке. Важнейшим параметром, используемым в моделях, является период полураспада, т.е. время, при котором концентрация вещества становится равной половине начальной (С0). В результате мы имеем две точки С0 и С0/2, по которым можно легко определить вид прямой и найти К0. Если же вещество разлается нелинейно, то следует использо‐ вать уравнения кинетику 1‐го или 2‐го порядка: Кинетика первого порядка: Ci =C0⋅exp(−k1*t); Кинетика второго порядка: Ci=C0/(1+k2*C0*t). Обычно, используют кинетику первого порядка. Это основано на предположении, что в почве имеются сорбционные центры разного порядка: первые сорбируют практически мгновенно – это сорбционные центры 1‐ го порядка, а потом сорбция протекает по законам кинетики, т.е. на сорбционных центрах 2‐го порядке. Вероятно, это приближает модели к реальности, однако заметно усложняет их. 5) Рост ???????????
Эмпирические – аппрокисмация типа регрессионные уравнения; полуэмпирические – то же но с учётом закономерностей Высокая общность этих моделей (стр-ра модели сохраняется, меняются только входные характеристики и параметры), могут быть использованы с целью проверки гипотез. Трудности: множественность разбития на блоки, число отражаемых связей м.б. разным. Степень подробности – обычно серия постепенно усложняющихся моделей. Важно помнить, что с увеличением сложности будет происходить увеличение точности, но в какой-то момент точность начнет падать, важно уловить эту точку перегиба – точку отпимума. Проверка адекватности (качественные критерии ( метод Сайерта: совпадение средней и совпадение по времени экстремумов, форма кривых, обращаем внимание на max и min, а так же поведение в этих точках; анализ остатков – разница между расчетными и экспериментальными значениями (должны быть распределены нормально, не зависеть от самой величины и не зависеть от времени); анализ коэффициента автокорреляции), количественные оценки (max относ ошибка имитации=max|Δxi/xi|; средняя относительная ошибка имитации Sr=1/N *∑ nj*∆j ; средняя квадратическая ошибка имитации= Нормализованная обьектная функция NOF=S2имит/Y̅. Вероятн. грубой ошибки: P=100*Nаномальн/Nвсего показатель Тейла 𝑈=√(1𝑁∗∑∆𝑥𝑖2)𝑁𝑖=1√(1𝑁∗∑(𝑥∗𝑖2)+(1𝑁∗∑𝑥𝑖2)𝑁𝑖=1𝑁𝑖=1, где x*i это экспериментальные данные, а xi- комплексные значения, U=0-полное совпадение до 1-плохое совпадение. Так же стоит помнить про критерий Фишера F=σвыб/σрег выб – вся выборка, рег – регрессия, чем F – выше тел лучше, если F-критерий с 3 параметрами меньше, чем F-критерий с 2-мя, то последний параметр – не значим и его отбрасываем. Критерий Вильямса-Клюта. Vi=0,5(Δ1+Δ2); Ui=Δ2-Δ1; a=Vi/Ui; p<0,05 графики отличаются; t>0 первый график лучше
В различных лабораторных экспериментах и при модельных расчетах было замечено, что анионы имеют некоторые особенности миграции. Эти вещества появляются на выходе из колонки раньше, чем не несущие заряда вещества. Образно говоря, для анионов поровое пространство, сквозь которое они мигрируют, несколько «сужается». Физики почв, давно указывали, что в почве имеется так называемый «нерастворяющий» объем, или «объем выталкивания» анионов, поскольку твердофазная стенка в почве, как правило, несет отрицательный заряд, как и анион. Происходит явление «отрицательной адсорбции» анионов.
Модели переноса вещества в почвах основаны на ковективно-диффузионном уравнении, модели солепереноса, модель FAUST. Уравнение конвективного переноса (уравнение неразрывности) связывает изменение концентрации растворимого вещества во времени со скоростью потока раствора в условном единичном капилляре, определяемой по уравнению Дарси, и изменение концентрации на границах рассматриваемого слоя. Конвективный перенос dc/dt=v*dc/dz, где v=qw/ε, где qw-макроскопическая скорость потока по Дарси. Уравнение конвективного переноса (уравнение неразрывности) связывает изменение концентрации растворимого вещества во времени со скоростью потока раствора в условном единичном капилляре, определяемой по уравнению Дарси, и изменение концентрации на границах рассматриваемого слоя. Например если рассмотреть абстрактную микропору и введем мигрант, то он будет двигаться вместе с основным движущимся составом (водой). Уравнение неразрывности для воды дθ/дt=дq/дz. Изменение влажности определенной толщи почвы во времени пропорционально изменению потока влаги в рассматриваемой толще колонки. В случае с солепереносом изменение концентрации солей во времени пропорционально изменению потока солей в рассматриваемой толще колонки и уравнение выглядит дc/дt=дqc/дz. Гидродинамическая дисперсия - это «размыв» фронта движущегося раствора, диффузия, происходящая вследствие неравномерности, сложности порового пространства почв, характеризуется коэффициентом гидродинамической дисперсии Dh. Коэффициент гидродинамической дисперсии, Dh, и коэффициент эффективной диффузии, Dэфф, объединяются в один, - коэффициент гидродинамической диффузии, D*. На величину Dh наибольшее влияние оказывают скорость движения потока в порах и структурное строение почвы. Полученное для расчета Dh уравнение Dh = λ|υ|n включает два параметра: λ – коэффициент, учитывающий дисперсию скорости потока в порах разного размера, называемый параметром гидродинамической дисперсии почвы или шагом смешения, возрастает с увеличением неоднородности упаковки почвенных частиц извилистости почвенных пор [см, м]. Показатель степени n, зависящий от структуры порового пространства, т.е. от плотности почвы и степени ее агрегированности. υ – поток раствора через единичный капилляр. При движении растворенных веществ в пористых средах, таких как почва, наблюдаются следующие явления: 1. нет четкой границы между поступающим раствором и почвенной влагой, происходит «размыв» фронта движущегося раствора; 2. при движении происходит непрерывное перемешивание раствора и почвенной влаги, в результате образуется расширяющаяся зона дисперсии (зона смешивания, переходная зона, шаг смешения); 3. интенсивность изменения концентрации индикатора больше в направлении движения потока по сравнению с направлением, перпендикулярным движению; 4. явление перемешивания, или «размыва», фронта движущегося раствора тем сильнее, чем выше скорость потока и значительнее дифференциация размеров пор. Около стенки твердой фазы образуется так называемая зона выталкивания аниона, или нерастворяющий для аниона объем пристеночной почвенной влаги. Наличие такого нерастворяющего объема приводит к более быстрому появлению аниона, и пик выходной кривой будет приходиться на значение такта, меньшее единицы.
Основу поглощения веществ растениями составляют два процесса: диффузия, которая вводится в модель в виде гидродинамической диффузии, и конвекция (модель Кушмана).
Эти 2 процесса
описываются уравнениями Где с – концентрация иона в поровом растворе, h D – коэффициент гидродинамической диффузии, r – радиус зоны, из которой происходит потребление вещества, v – макроскопическая скорость потока раствора (т.е. усредненная скорость движения в капиллярах почвы). Кроме того, происходит обмен ионов в растворенном и поглощенном состоянии по механизму моментальной линейной адсорбции Cs=Kd*C, где сs – концентрация иона в поглощенном состоянии, Kd – константа распределения. Этот процесс формирует фактор дополнительного «источника‐стока» Js. В целом подток веществ к корню можно выразить в виде уже знакомого нам конфективно‐диффузионного уравнения, но записанного в цилиндрических координатах, так как поток к центрально расположенному корню происходит по радиусу:
Чувствительность модели – это скорость изменения искомой переменной состояния в зависимости от относительного изменения начальных, граничных условий и параметров экспериментального обеспечения. Анализ чувствительности – исследование изменения поглощения иона корнем при попеременном изменении каждого из параметров модели.
1) Под застойным поровым пространством понимают внутриагрегатное (внутрипедное) пространство, а под проточным – межагрегатное (межпедное). При описании конвективно‐диффузионного переноса (КДП) сорбирующихся веществ в хорошо агрегированных почвах часто не удается получить удовлетворительное приближение рассчитанной динамики вещества к экспериментальной. Получается, что вещество, пусть и в небольшом количестве, но проникает быстрее и глубже, чем это предписывают законы равновесной сорбции. Учет взаимодействия подвижной и относительно неподвижной влаги двух зон порового пространства возможен введением в уравнение дополнительного члена – f, учитывающего распределение сорбционных центров в проточной и застойной зонах: Сs = f⋅Сsп + (1 – f)Csз, где Cs – общее количество сорбированного вещества в твердой фазе, ⋅Сsп и Csз – количество сорбированного вещества в проточной и застойной зонах порового пространства соответственно. При нулевом значении параметра f сорбция рассматривается только в застойных зонах, а при f=1 – только в проточных. 2) Если время ионообмена между твердой и жидкой фазами почвы пренебрежимо мало по сравнению со временем прохождения потока влаги через почвенный слой, для простых ионов используют уравнение линейной равновесной сорбции: Сs = k0⋅с, где k0 – константа сорбции или коэффициент распределения вещества между жидкой и твердой фазами почвы, а с – концентрация вещества в растворе [моль/л]. 3) В различных лабораторных экспериментах и при модельных расчетах было замечено, что анионы имеют особенности миграции. Эти вещества появляются на выходе из колонки раньше, чем не несущие заряда вещества. Образно говоря, для анионов поровое пространство, сквозь которое они мигрируют, несколько «сужается». Физики почв, давно указывали, что в почве имеется так называемый «нерастворяющий» объем, или «объем выталкивания» анионов, поскольку твердофазная стенка в почве, как правило, несет отрицательный заряд, такой же как и анион. Происходит явление «отрицательной адсорбции» анионов. Влага, составляющая часть заполняющей пору, не содержит анионы и не является для них проводящим пространством. Ее нужно исключить из проводящего ионы порового пространства. Эта влажность была названа влажностью нерастворяющего объема – θ [безразмерная величина или см3/см3].
4) Для упрощения модели с 2 типами сорбции предлагается разделить все типы взаимодействия на два: 1. Мгновенное, описываемое уравнением линейной равновесной сорбции (0-го порядка); 2. Кинетическое, с линейной изотермой сорбции 1‐го порядка.
Подход для описания сложного процесса сорбции во многом формальный, никто не знает методов определения числа (концентрации) центров мгновенного (равновесного) и кинетического (динамического) равновесия, однако, этот подход применяется повсеместно в разных моделях. Мгновенный
обмен приписывается центрам сорбции
1‐го
типа и выражается уравнением:
Для
описания кинетического взаимодействия
центров 2‐го
типа используется уравнение
неравновесного обмена вещества,
которые находятся в растворенном и
сорбированном виде:
Для описания динамической сорбции используют уравнение кинетики 1‐го порядка (функция экспоненциально убывающая). Также считается, что сорбция на сорбционных центрах 1‐го типа происходит мгновенно (в уравнении нет параметра времени), это сорбция всегда равновесный процесс. На центрах 2‐го типа, которые сорбируют по кинетике 1‐го порядка, происходит неравновесная динамическая сорбция.
За последние годы в практике оценки концентраций пестицидов в окружающей среде стали широко использоваться математические модели, разработанные в Европейском Союзе (MACRO, PEARL, PELMO), в сочетании со стандартными сценариями входных данных - почвенно-климатических условий, характеризующих основные регионы Западной Европы.
Диффузия— процесс переноса материи или энергии из области с высокой концентрацией в область с низкой концентрацией (против градиента концентрации). Движение ионов происходит в извилистом поровом пространстве почв, заполненном раствором. Поэтому используют понятие «эффективного коэффициента диффузии», Дэфф, учитывающего извилистость порового пространства почв и влажность почвы. В результате эти два коэффициента, отражающих процессы диффузии и гидродинамической дисперсии, объединяют в один коэффициент, называемый коэффициентом конвективной диффузии D*: D*=Dэфф+Dh. Уравнение переноса растворимых веществ будет выглядеть следующим образом: qc=-D* (d2с/dz2)+υ(dc/dz). С учетом того, что перенос веществ осуществляется через поровое пространство, заполненное водой, необходимо ввести в уравнение и объемную влажность почвы (θ): θdc/dt=-D* θ(d2с/dz2)+υ(dc/dz). Эффективная диффузия – диффузия, происходящая в заполненном почвенной влагой поровом пространстве почв. Отличается от молекулярной диффузии в растворах вследствие извилистости порового пространства и реальной влажности почв и характеризуется коэффициентом эффективной диффузии, Dэфф. Конве́кция — явление переноса теплоты в жидкостях или газах путем перемешивания самого вещества (как вынужденно, так и самопроизвольно). Существует т. н. естественная конвекция, которая возникает в веществе самопроизвольно при его неравномерном нагревании в поле тяготения Гидродинамическая дисперсия - это «размыв» фронта движущегося раствора, диффузия, происходящая вследствие неравномерности, сложности порового пространства почв, характеризуется коэффициентом гидродинамической дисперсии Dh. Коэффициент гидродинамической дисперсии, Dh, и коэффициент эффективной диффузии, Dэфф, объединяются в один, - коэффициент гидродинамической диффузии, D*. На величину Dh наибольшее влияние оказывают скорость движения потока в порах и структурное строение почвы. Полученное для расчета Dh уравнение Dh = λ|υ|n включает два параметра: λ – коэффициент, учитывающий дисперсию скорости потока в порах разного размера, называемый параметром гидродинамической дисперсии почвы или шагом смешения, возрастает с увеличением неоднородности упаковки почвенных частиц извилистости почвенных пор [см, м]. Показатель степени n, зависящий от структуры порового пространства, т.е. от плотности почвы и степени ее агрегированности. υ – поток раствора через единичный капилляр
Кроме того, при
движении вещества могут происходить
процессы, связанные с его выпадением
в осадок, потреблением растениями, и
др. — процессы его расхода, стока.
Либо, напротив, его количество может
увеличиваться за счет растворения
осадков, притока сбоку и пр. - процессы
притока, источника. Они обозначаются
как ±J(z,t)
- член, характеризующий возникновение
(+) или потребление (-) мигранта, или,
как иногда говорят, «источник/сток».
Он будет характеризоваться изменением
концентрации во времени и иметь ту же
размерность [моль/см3сут].
Если же происходит сорбция вещества,
то в уравнение переноса мигранта
следует ввести концентрацию вещества
в адсорбированной фазе (S, [моль/г]).
Или, учитывая, что все процессы, в том
числе и сорбции происходят в объеме
почвы [моль/см3],
она будет характеризоваться величиной
S· ρb,
где ρb
- плотность почвы [г/см3].
В итоге мы получим уравнение, которое
будет описывать все отмеченные явления
передвижения растворимых веществ в
почве. Оно носит название уравнения
конвективно-диффузионного переноса
и выглядит следующим образом:
Модели переноса вещества в почвах основаны на ковективно-диффузионном уравнении, модели солепереноса, модель FAUST. Уравнение конвективного переноса (уравнение неразрывности) связывает изменение концентрации растворимого вещества во времени со скоростью потока раствора в условном единичном капилляре, определяемой по уравнению Дарси, и изменение концентрации на границах рассматриваемого слоя. Конвективный перенос dc/dt=v*dc/dz, где v=qw/ε, где qw-макроскопическая скорость потока по Дарси. Уравнение конвективного переноса (уравнение неразрывности) связывает изменение концентрации растворимого вещества во времени со скоростью потока раствора в условном единичном капилляре, определяемой по уравнению Дарси, и изменение концентрации на границах рассматриваемого слоя. Например если рассмотреть абстрактную микропору и введем мигрант, то он будет двигаться вместе с основным движущимся составом (водой). Уравнение неразрывности для воды
Изменение
влажности определенной толщи почвы
во времени пропорционально изменению
потока влаги в рассматриваемой толще
колонки. В случае с солепереносом
изменение концентрации солей во
времени пропорционально изменению
потока солей в рассматриваемой толще
колонки и уравнение выглядит
При движении растворенных веществ в пористых средах, таких как почва, наблюдаются следующие явления: 1. нет четкой границы между поступающим раствором и почвенной влагой, происходит «размыв» фронта движущегося раствора; 2. при движении происходит непрерывное перемешивание раствора и почвенной влаги, в результате образуется расширяющаяся зона дисперсии (зона смешивания, переходная зона, шаг смешения); 3. интенсивность изменения концентрации индикатора больше в направлении движения потока по сравнению с направлением, перпендикулярным движению; 4. явление перемешивания, или «размыва», фронта движущегося раствора тем сильнее, чем выше скорость потока и значительнее дифференциация размеров пор. Около стенки твердой фазы образуется так называемая зона выталкивания аниона, или нерастворяющий для аниона объем пристеночной почвенной влаги. Наличие такого нерастворяющего объема приводит к более быстрому появлению аниона, и пик выходной кривой будет приходиться на значение такта, меньшее единицы.
Явление приемущественных потоков
Параметры переноса солей: D*-гидродин диффузия, q*-влажность нерастворяющего объема (при движении анионов), Ксорбции – константа распрделения (при движ сорбирующихся в-в), к0,к1,к2 – константы равновесия.
MACRO, PEARL, PELMO.Основную роль в транспорте пестицидов в окружающей среде играет вода и поэтому, модели предполагают использование в качестве одних из входных параметров гидрофизические свойства почв, от которых во многом зависит точность прогноза поведения пестицидов в почвах. Настраивая гидрофизический блок моделей, можно добиться более адекватного прогноза, учитывающего региональную специфику почв. Сравнение прогнозной и экспериментальной динамики содержания имидаклоприда в почвах показало, что в целом модели идентично предсказывали остаточные количества инсектицида в почвенной толще. Однако модель MACRO количественно более точно прогнозировала профильное распределение имидаклоприда и его попадание в лизиметрические воды. Модель PELMO. Состоит из отдельных блоков: почва, вещество( учитываются константы кинетики К0,К1,К2), растения и метеоусловия. Учитывается количество и свойства слоев (ОГХ, Кр).
2.1) Процессы ионного обмена. В химии их классифицируют как «гомогенный» и «гетерогенный». Гомогенный ионный обмен происходит в водной среде в отсутствии активной твердофазной поверхности (поверхности обмена). Для применения к гомогенному ионному обмену количественных подходов используются методы термодинамики равновесных процессов. Зная константы равновесия и активности ионов в растворах, можно использовать термодинамические уравнения равновесия. На этом принципе построены модели расчета различных почвенных реакций, таких как диссоциация угольной кислоты, диссоциация бикарбонат иона, диссоциации воды и т.д., что позволяет рассчитывать карбонатно‐кальциевые равновесия в почвах, а также процессы осаждения/растворения твердой фазы (растворение гипса, кальцита, гидрооксида железа и пр.).
2.2) Если в растворе присутствует ионообменник, например, почвенный коллоидный комплекс, это значительно осложняет ситуацию. Классические методы, основанные на гипотезе об однородности обмена, в этом случае не работают (гетерогенный обмен). Поэтому в химии почв при моделировании и расчетах катион‐обменных реакций используют не термодинамические уравнения, а полуэмпирические модели селективного обмена. Принимается, что активность соединения «катион‐обменная позиция» пропорциональна его доле в суммарном заряде обменных катионов. В
российской школе химии почв
катион‐обменные
реакции обычно рассчитывают по Гапону
(известный физико‐химик,
работавший в Тимирязевской академии,
оставивший весьма заметный след
работами по изучению обменных реакций
в почве), либо по Венслоу, реже по
Никольскому. Следует отметить, что большинство современных моделей для описания обменных процессов используют именно подход Гапона, где А и В пара обменных катионов с зарядами zA и zB, sB a – активность соединения «Катион В – ионообменный комплекс», а sA a – активность соединения «Катион А – ионообменный комплекс».
|
|||||||||||||||||||||||||||||||||||||||||||||||||||

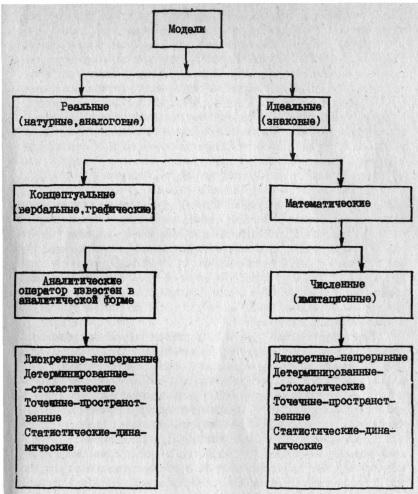
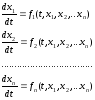
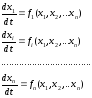
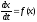
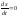
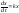
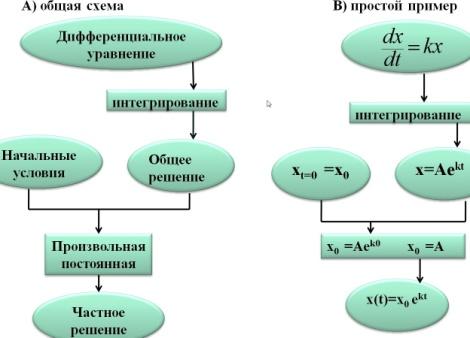
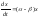
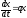
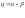
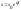

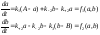
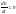

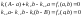





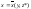 .
Таким образом, благодаря учету иерархии
времен, исходную систему из трех
дифференциальных уравнений удается
свести к одному дифференциальному
уравнению для переменной y:
.
Таким образом, благодаря учету иерархии
времен, исходную систему из трех
дифференциальных уравнений удается
свести к одному дифференциальному
уравнению для переменной y:
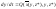 .
Строгим обоснованием применимости
этого метода является теорема Тихонова.
.
Строгим обоснованием применимости
этого метода является теорема Тихонова.
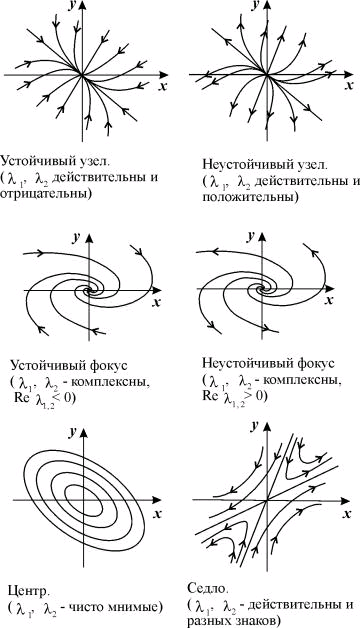

 Atractor-
множество точек или подпространств
в фазовом
Atractor-
множество точек или подпространств
в фазовом


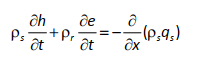
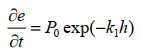
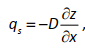
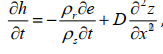
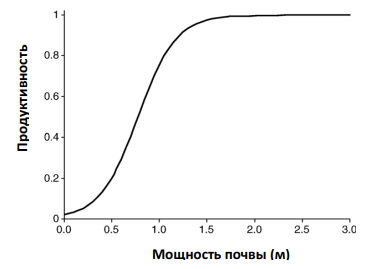
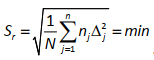


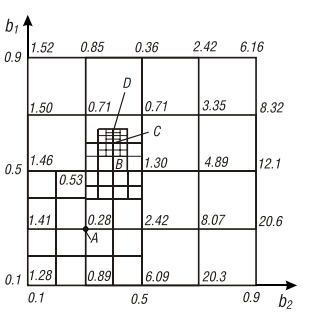
 Заметим,
что во время операции сканирования
мы сделали
очень важный шаг: мы начали
наши расчеты с конкретных значений
b1
и b2.
Мы их задали равными 0.3. Эти значения
называют «начальные
приближения».
Задавать их – большое искусство. Если
их задать совсем другими, мы окажемся
совсем в другом месте рассматриваемого
поля и по мере движения («дробления
сетки») можем оказаться не в генеральном
минимуме, а в так называемом «локальном
минимуме», что будет серьезной ошибкой.
Даже современные расчетные программы
в этом случае «зависают» и не находят
нужного решения.
Заметим,
что во время операции сканирования
мы сделали
очень важный шаг: мы начали
наши расчеты с конкретных значений
b1
и b2.
Мы их задали равными 0.3. Эти значения
называют «начальные
приближения».
Задавать их – большое искусство. Если
их задать совсем другими, мы окажемся
совсем в другом месте рассматриваемого
поля и по мере движения («дробления
сетки») можем оказаться не в генеральном
минимуме, а в так называемом «локальном
минимуме», что будет серьезной ошибкой.
Даже современные расчетные программы
в этом случае «зависают» и не находят
нужного решения.

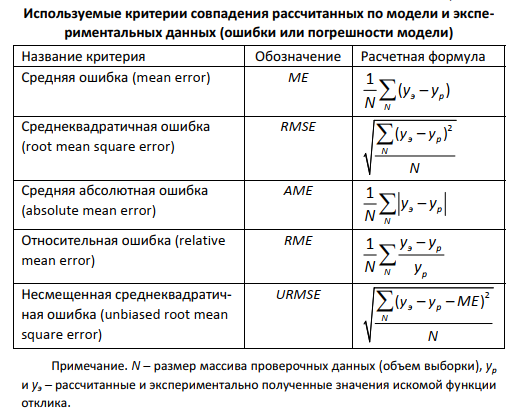
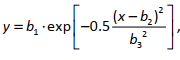
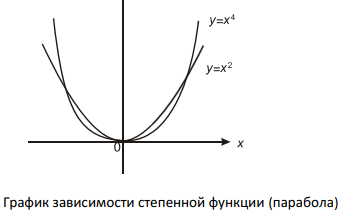

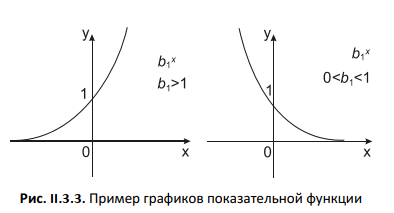

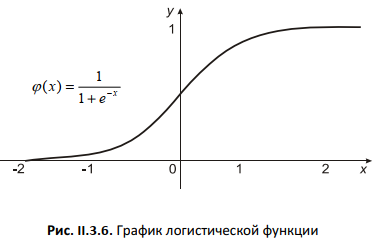












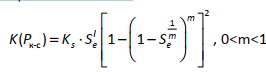














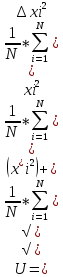 ,
где x*i
это экспериментальные данные, а xi-
комплексные значения, U=0-полное
совпадение до 1-плохое совпадение. Так
же стоит помнить про критерий Фишера
F=σвыб/σрег
выб – вся выборка, рег – регрессия,
чем F
– выше тел лучше, если F-критерий
с 3 параметрами меньше, чем F-критерий
с 2-мя, то последний параметр – не
значим и его отбрасываем.
,
где x*i
это экспериментальные данные, а xi-
комплексные значения, U=0-полное
совпадение до 1-плохое совпадение. Так
же стоит помнить про критерий Фишера
F=σвыб/σрег
выб – вся выборка, рег – регрессия,
чем F
– выше тел лучше, если F-критерий
с 3 параметрами меньше, чем F-критерий
с 2-мя, то последний параметр – не
значим и его отбрасываем.