
Задача № 4
Имеется следующая информация о товарообороте торгового предприятия за 2001 – 2005 годы:
|
Годы |
2001 |
2002 |
2003 |
2004 |
2005 |
|
Товарооборот, (млн. руб.) |
40,2 |
48,3 |
54,4 |
60,2 |
64,8 |
Для анализа динамики товарооборота торгового предприятия в 2001 – 2005 гг. определите основные показатели динамики:
абсолютные приросты, темпы роста и темпы прироста (на цепной и базисной основе);
средние показатели динамики;
возможный размер товарооборота в 2008 году (используя средний абсолютный прирост);
Постройте график, характеризующий интенсивность динамики товарооборота. Полученные результаты оформите в виде статистической таблицы.
Произведите анализ общей тенденции развития товарооборота:
исходные и выровненные уровни ряда динамики нанесите на график и сделайте выводы;
используя построенную модель, произведите прогнозирование возможного размера товарооборота в 2008 г.;
сравните полученные результаты в пунктах 1.3. и 2.2.
Решение.
1. Проанализируем динамику товарооборота торгового предприятия
1.1
1) Абсолютный прирост
∆=Yi – Yi-1, где
Yi – значение показателя текущего года;
Yi-1 – значение показателя базисного или предыдущего года.
2) Темп роста
Тр=100%*Yi/Yi-1
3) Темп прироста
Тп=Тр-100%
Все расчеты представим в виде таблицы (табл. 6).
Таблица 6
Показатели динамики товарооборота торгового предприятия
|
Год |
Товарооборот, млн. руб. |
Абсолютный прирост |
Темп роста |
Темп прироста | |||
|
цепной |
базисный |
цепной |
базисный |
цепной |
базисный | ||
|
2001 |
40,2 |
|
|
|
|
|
|
|
2002 |
48,3 |
8,1 |
8,1 |
120,15 |
120,15 |
20,15 |
20,15 |
|
2003 |
54,4 |
6,1 |
14,2 |
112,63 |
135,32 |
12,63 |
35,32 |
|
2004 |
60,2 |
5,8 |
20 |
110,66 |
149,75 |
10,66 |
49,75 |
|
2005 |
64,8 |
4,6 |
24,6 |
107,64 |
161,19 |
7,64 |
61,19 |
1.2. Средний уровень ряда определяется по формуле:
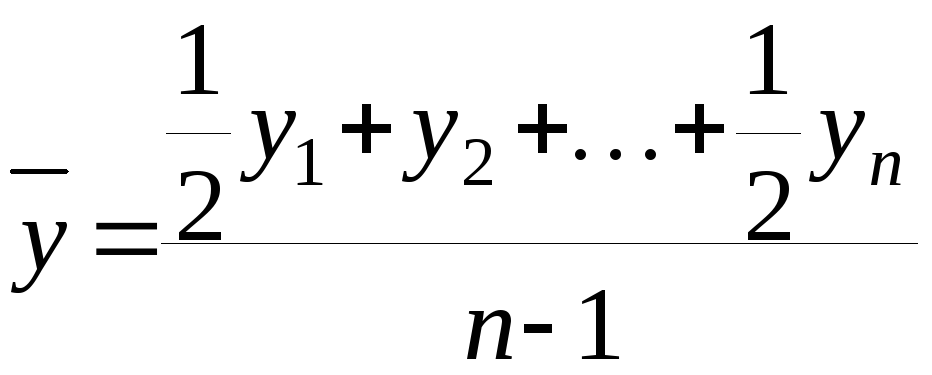
где:
![]() – уровни ряда динамики соответственно
на 1-ю, 2-ю, …,n-ю
даты времени.
– уровни ряда динамики соответственно
на 1-ю, 2-ю, …,n-ю
даты времени.
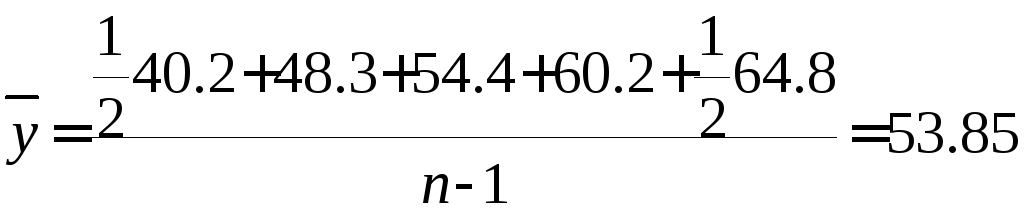
Для
определения среднего (среднегодового)
темпа роста
![]() по
абсолютным уровням ряда используется
формула:
по
абсолютным уровням ряда используется
формула:
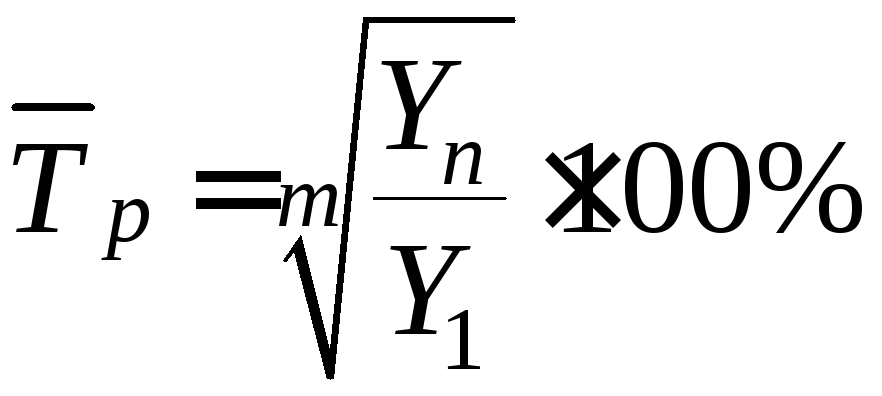
где:
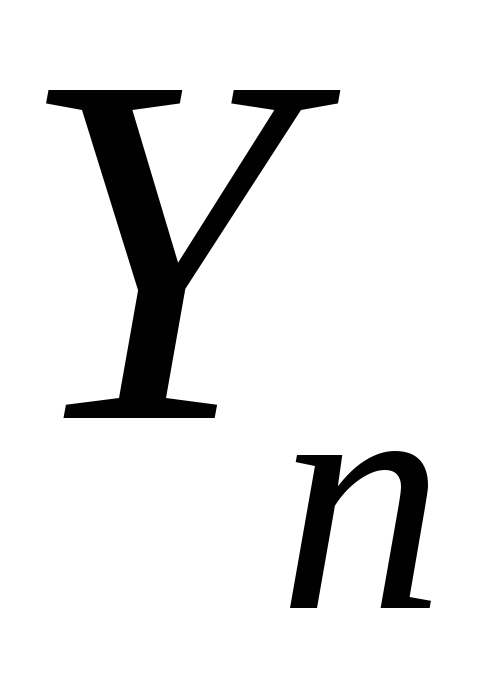 – конечный уровень
ряда;
– конечный уровень
ряда;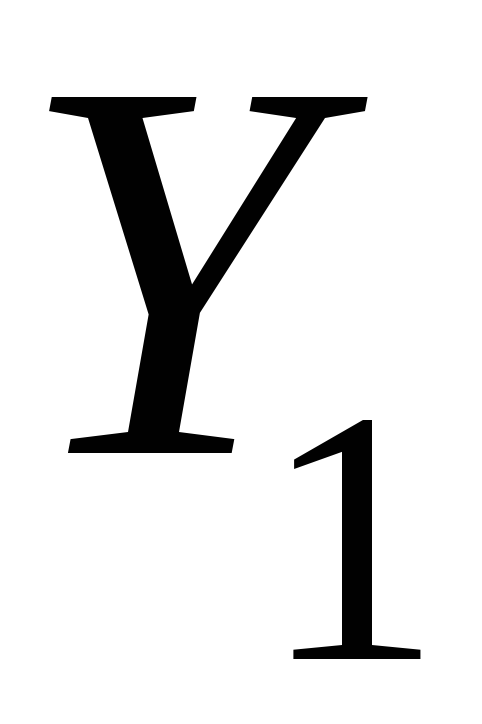 – базисный
(начальный) уровень ряда;
– базисный
(начальный) уровень ряда;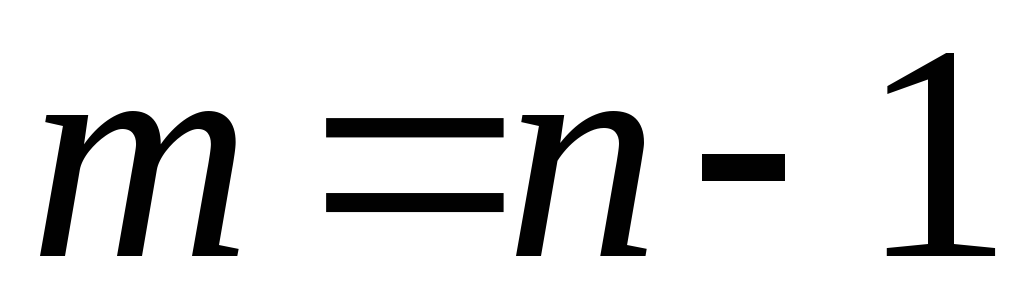 – число
субпериодов в изучаемом ряду динамики.
– число
субпериодов в изучаемом ряду динамики.
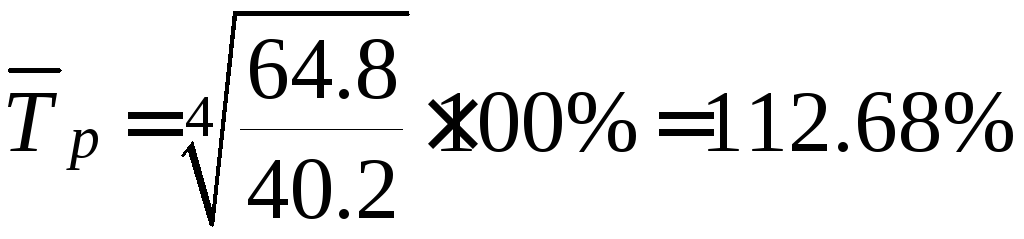
Средний (среднегодовой) абсолютный прирост можно определить и по абсолютным уровням ряда динамики:
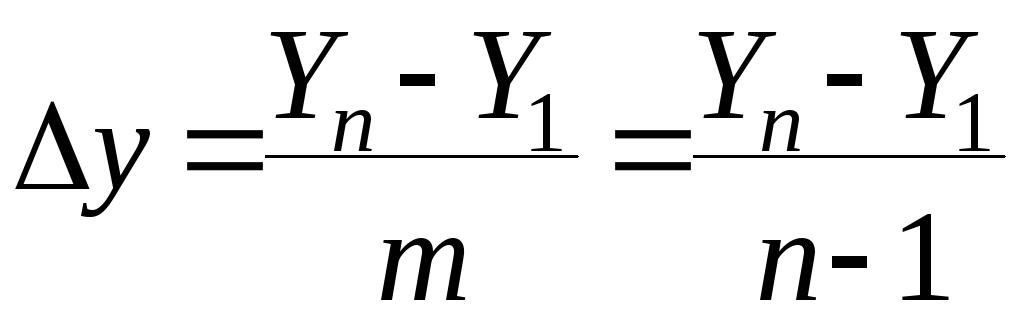
где:
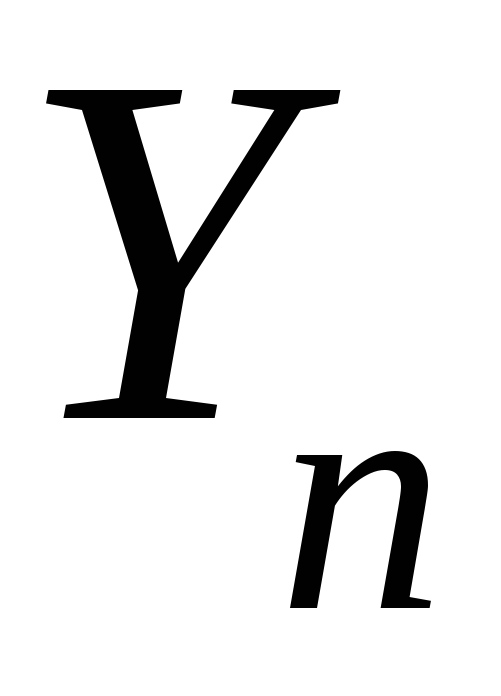 – конечный уровень
ряда динамики;
– конечный уровень
ряда динамики;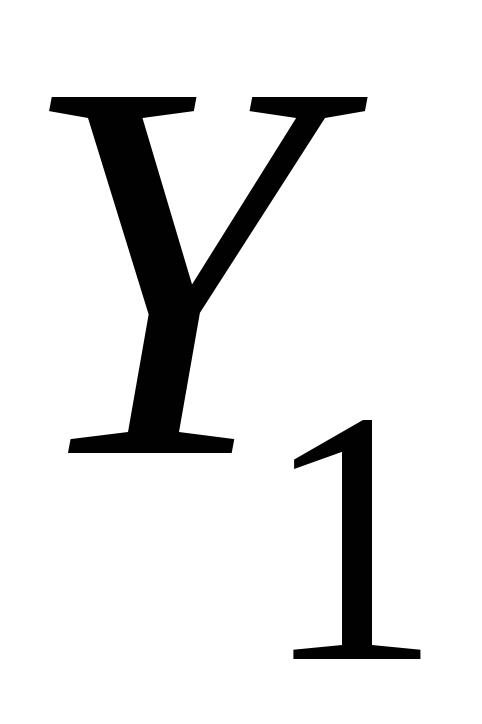 – базисный
начальный уровень ряда динамики;
– базисный
начальный уровень ряда динамики;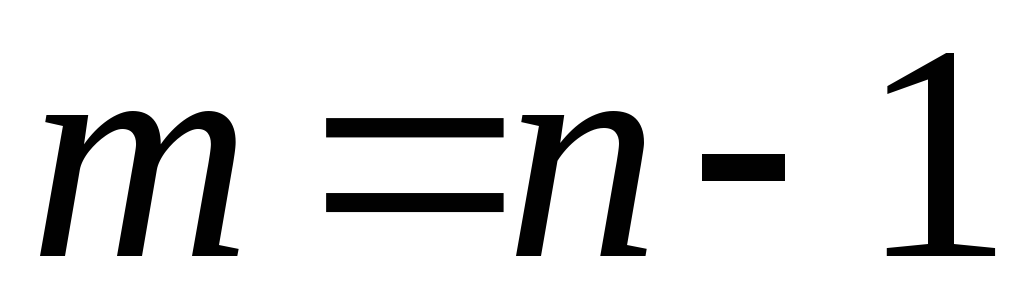 – число субпериодов
в изучаемом интервале времени.
– число субпериодов
в изучаемом интервале времени.
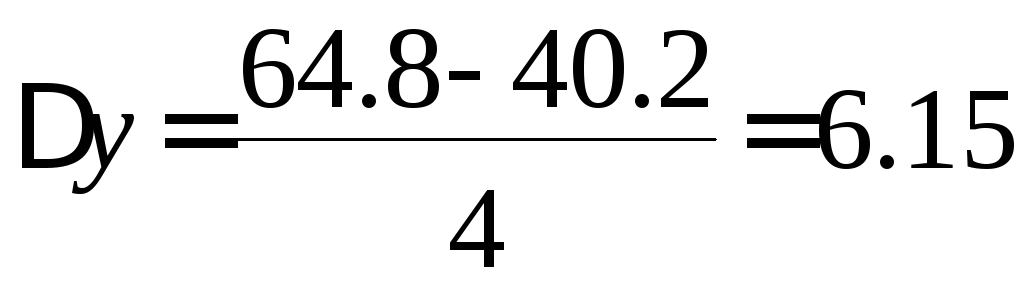
1.3. Для
определения возможного размера
товарооборота по среднему абсолютному
приросту
![]() применяют
формулу:
применяют
формулу:
![]()
где:
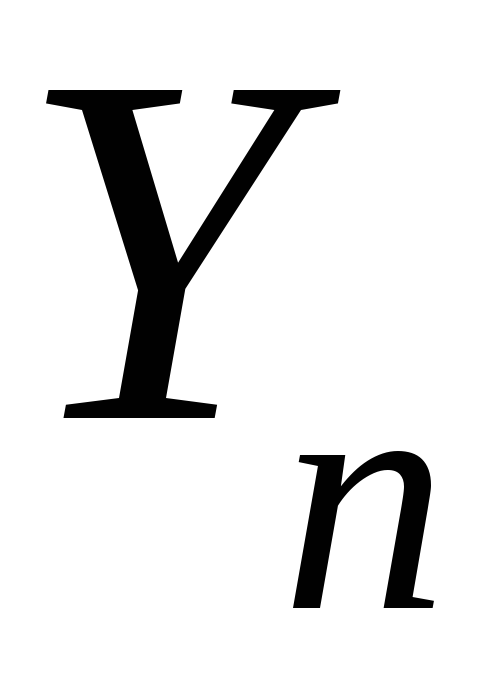 – конечный уровень
ряда динамики;
– конечный уровень
ряда динамики;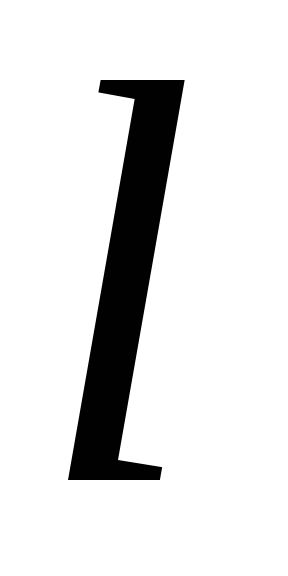 – срок прогноза
(упреждения).
– срок прогноза
(упреждения).
![]() млн. руб.
млн. руб.
Для
характеристики интенсивности динамики
товарооборота используется показатель
темпа наращивания
![]() :
:
![]()
Расчеты представлены в табл. 7
Таблица 7
Темп наращивания ряда динамики
|
Год |
Товарооборот, млн. руб. |
Абсолютный прирост |
Темп наращивания |
|
2001 |
40,2 |
0 |
0 |
|
2002 |
48,3 |
8,1 |
0,201 |
|
2003 |
54,4 |
14,2 |
0,353 |
|
2004 |
60,2 |
20 |
0,498 |
|
2005 |
64,8 |
24,6 |
0,612 |
График интенсивности динамики товарооборота представлен на рис. 3.
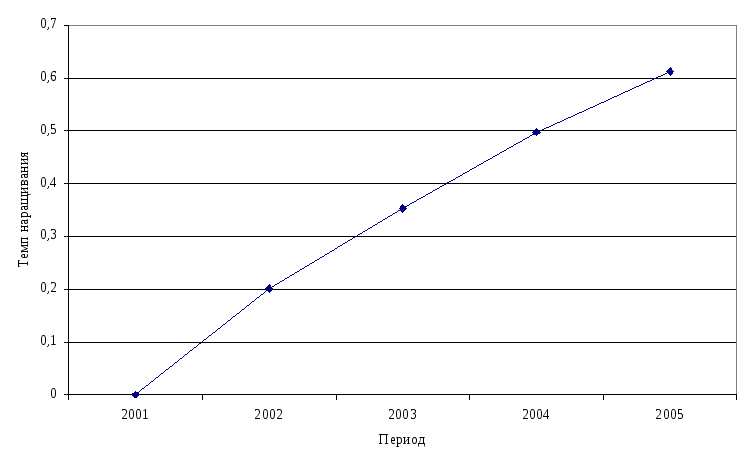
Рис. 3. Интенсивность динамики товарооборота
2. Анализ общей тенденции развития товарооборота
Для применения метода аналитического выравнивания, необходимо построить линию тренда и найти ее уравнение.
Линия тренда построим с помощью инструментов электронной таблицы Excel.
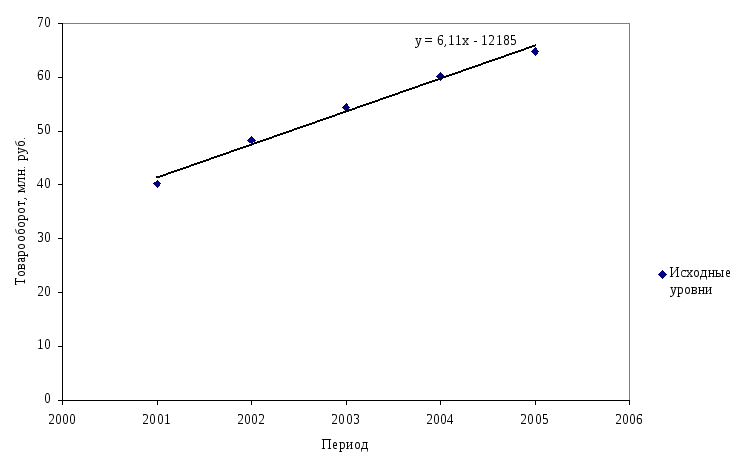
Рис. 4. Исходные и выровненные уровни ряда
Спрогнозируем возможный размер товарооборота в 2008 г.
![]()
Таким образом, сравнивая прогнозные значения товарооборота полученные при помощи среднего абсолютного прироста (83,25) и метода аналитического выравнивания (83,88), видим что данные значения близки друг к другу.
