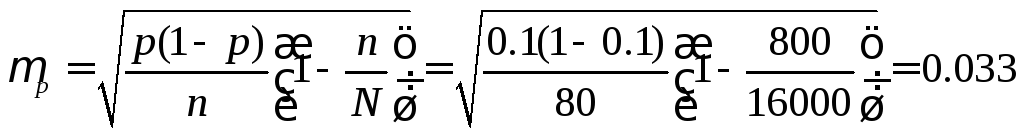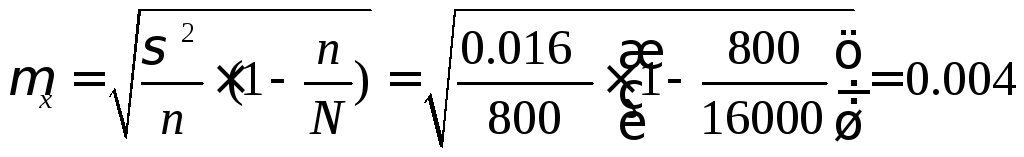Задача № 2

Используя построенный в задаче № 1 интервальный ряд распределения магазинов по размеру товарооборота, определите:

1. среднее квадратическое отклонение;

2. коэффициент вариации;

3. модальную величину;

4. медиану.

Постройте гистограмму распределения и сделайте выводы.

Решение.

Среднеквадратическое отклонение определяется по формуле:

,

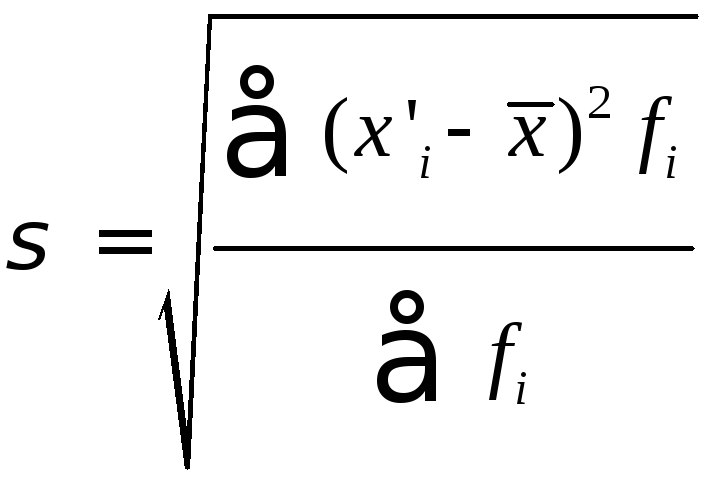где

- среднее арифметическое исследуемой совокупности;

- среднее значение группы;

количество магазинов в группе.

Для расчета среднеквадратического отклонения составим вспомогательную таблицу (табл. 3).

Таблица 3

Рабочая таблица

Группа магазинов	Число магазинов
1,3 - 14,68	8	4,450	280,563	2244,5
14,68 - 28,05	4	22,875	2,806	11,2225
28,05 - 41,43	2	30,950	95,062	190,125
41,43 - 54,8	4	48,150	726,303	2905,21
Итого:	18	106,425	1104,733	5351,058

Среднеквадратическое отклонение:

Коэффициент вариации определим как

Мода определяется по формуле:

где - начало модального интервала;

- частота, соответствующая модальному интервалу;

- предмодальная частота;

- послемодальная частота.

Для расчета составим рабочую таблицу (табл. 4):

Таблица 4

Рабочая таблица

№ интервала п/п	Товарооборот (млн. руб.)	Число магазинов
1	1,3 - 14,68	8
2	14,68 - 28,05	4
3	28,05 - 41,43	2
4	41,43 - 54,8	4
5	1,3 - 14,68	8
	Итого:	18

Таким образом, наибольшая частота соответствует интервалу 1,3 - 14,68 млн. руб. следовательно в нем находится мода.

По данным табл. 4 построим гистограмму распределения магазинов по размеру товарооборота (рис. 1).

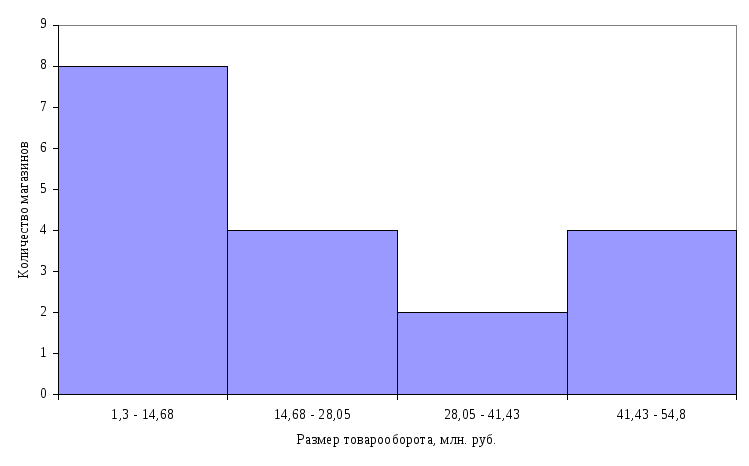
Рис. 4.1. Гистограмма распределения магазинов по размеру товарооборота

Медиана определяется по формуле:

,

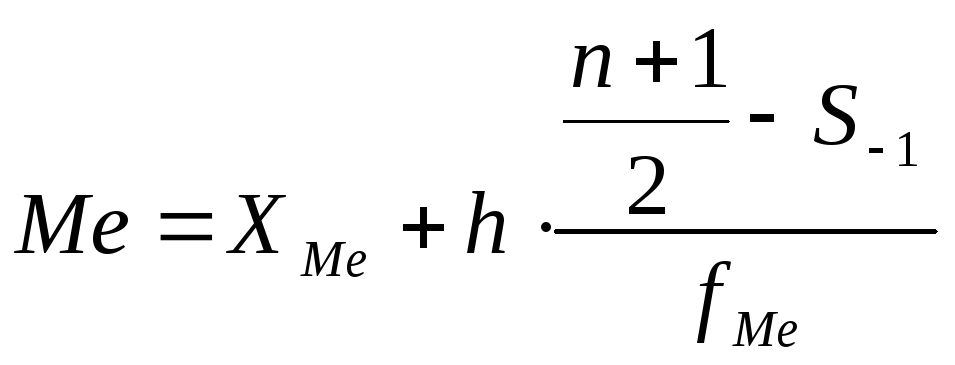где - нижняя граница медианного интервала,

- величина интервала;

- накопленная частота интервала, предшествующего медианному;

- частота медианного интервала.

Для определения медианы построим кумулятивную кривую.

Данные для построения кривой представлены в таблице 5

Таблица 5

Размер товарооборота, млн. руб.	Накопленная частота
1,3 - 14,68	8
14,68 - 28,05	12
28,05 - 41,43	14
41,43 - 54,8	18
Итого:	18

Накопленная частота показывает сколькое единиц совокупности имеют значения признака не больше, чем рассматриваемое значение, и определяется последовательным суммированием частот интервалов.

По данным табл. 5 построим кумулятивную кривую (рис. 2).

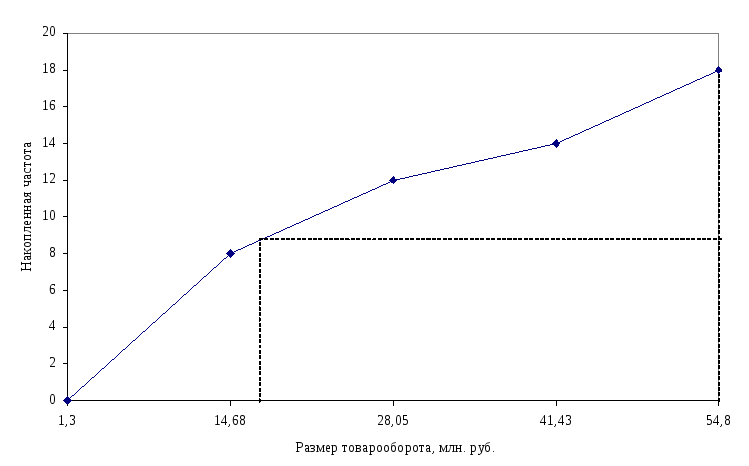
Рис. 2. Кумулятивная кривая.

Из рис. 2. видим, что медианным является интервал 14,68 – 28,05 млн. руб.

Следовательно, медиана равна:

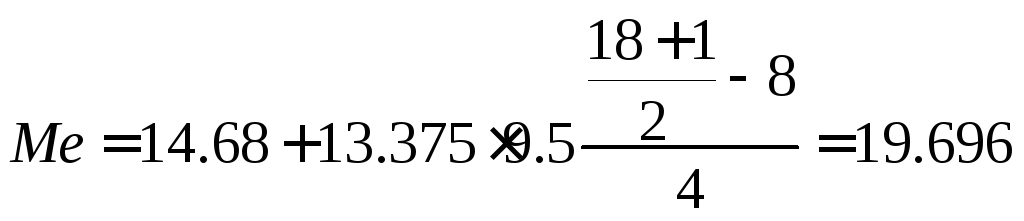
Для рассмотренного ряда распределения, значения моды и медианы сильно различаются, и находятся в разных интервала, следовательно, мы имеем не симметричный ряд распределения.

Задача № 3

Проведено 5-процентное обследование качества поступившей партии товара. В выборку попало 800 единиц (на основе механического способа отбора), из которых 80 единиц оказались нестандартными. Средний вес одного изделия в выборе составил 18,6 кг, а дисперсия – 0,016.

Определите:

1. С вероятностью 0,997 пределы, в которых находится генеральная доля нестандартной продукции.

2. С вероятностью 0,954 пределы, в которых находится средний вес одного изделия во всей партии товара.

По полученным результатам сделайте выводы.

Решение.

1) Определим долю нестандартной продукции.

,

где - количество нестандартных изделий;

N – объем выборки.

Ошибка выборки доли Используя таблицу значений функции Лапласа, найдем что: для вероятности Ф(t)=0,997 t=3,00 [1, стр. 167]

Нижняя граница доверительного интервала

Верхняя граница доверительного интервала

2) Определим пределы, в которых находится средний вес одного изделия во всей партии товара.

Ошибка средней величины

Используя таблицу значений функции Лапласа, найдем что: для вероятности Ф(t)=0,954 t=2,00 [1, стр. 167] Нижняя граница доверительного интервала

Верхняя граница доверительного интервала