
- •Лекция 1
- •Лекция 2 Визуализация течений. Компьютерная графика.
- •Лекция 5 Моделирование неравновесных химических процессов
- •2.Уравнение состояния для смеси
- •3. Изменение концентраций компонент
- •Лекция 11
- •5. Метод Гаусса-Зегеля.
- •6. Многосеточный алгоритм.
- •1) Алгебраические методы
- •2) Интегральные методы
- •3) Дифференциальные методы
- •4) Вариационные методы
Лекция 11
Методы решения систем алгебраических уравнений.
![]() ,
,
![]()

![]()
![]() ,
j=1,2,…Nx;
k=1,2,…Ny
,
j=1,2,…Nx;
k=1,2,…Ny
![]() - система линейных уравнений
- система линейных уравнений
В трехмерном случае
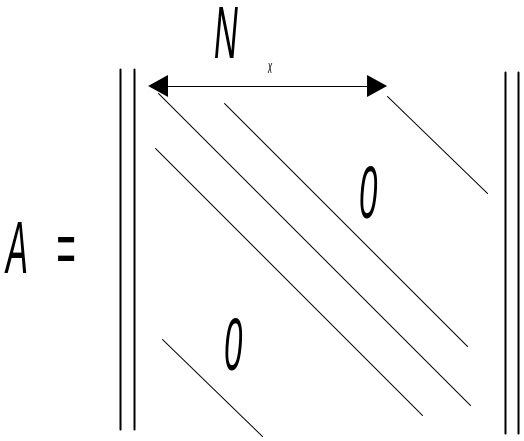


5 диагоналей
Пример.
![]() ,
u(0)=0, u(1)=0
,
u(0)=0, u(1)=0
1)
![]()
![]() ,
,
![]()
![]() - бесконечное число собственных значений.
- бесконечное число собственных значений.
2)
![]() - разностная система
- разностная система
![]()
![]()
![]()
![]()
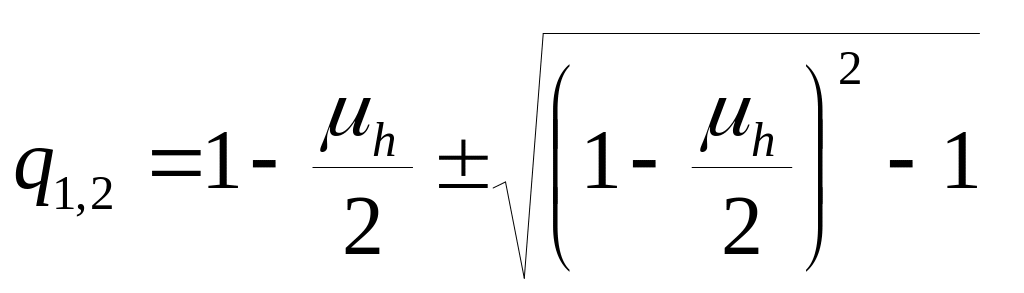
![]()
![]() (по теореме Виета)
(по теореме Виета)
![]()
![]()
![]()
![]()
![]() ;
;
![]() ,
k=1,…,N
,
k=1,…,N
![]() ,
,
![]() ,
,
k=1,…,N
,
,
k=1,…,N
 ,
,
![]()
![]()
![]()
![]() - конечное число собственных значений
- конечное число собственных значений
спектр собственных значений разностного оператора.
![]()
![]()
![]() -
система алгебраических уравнений
-
система алгебраических уравнений
![]() - норма матрицы А
- норма матрицы А
![]()
![]()
![]()
относительная погрешность
![]() - число обусловленности матрицы А
- число обусловленности матрицы А
Свойства: 1)
![]() ,
,
2)
![]() ,
,
3)
![]() Доказательство:
Доказательство:
![]() !
!
![]() - относительная погрешность, где
- относительная погрешность, где
![]() -
точность одного вычисления.
-
точность одного вычисления.
![]() Real:
Real:
![]()
Double:
![]()
![]() - относительная погрешность численного
решения системы уравнений.
- относительная погрешность численного
решения системы уравнений.

![]()
![]()
![]()
погрешность аппроксимационных вычислений
Real:
![]()
Double:
![]()
Прямые методы решения линейных алгебраических уравнений (метод Гаусса).
а) 2-х мерная задача.
Матрица блочной структуры

![]() - уравнение каждого блока.
- уравнение каждого блока.
Оценим необходимые ресурсы компьютера для решения системы методом блочной прогонки:
1) Память:
число блоков в матрице A
- N, в каждом блоке
-
![]() элементов
элементов
![]()
2) Число операций:
![]()
нахождение обратной
матрицы размером
![]()
б) 3-х мерная задача.
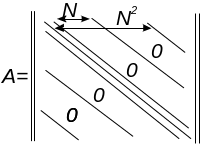
![]() - память
- память
![]() -
операции.
-
операции.
![]() ,
j=1,2,…N;
k=1,2,…N
,
j=1,2,…N;
k=1,2,…N
![]() - cистема алгебраических
уравнений
- cистема алгебраических
уравнений
![]() - итерационная процедура.
- итерационная процедура.
![]()
![]() при
при
![]()
Здесь B – переобуславливатель, - ускоритель итерационного процесса
В – 3-х диагональная матрица
Число необходимых итераций
 ,
где спектр собственных значений
,
где спектр собственных значений
![]() ,
m зависит от способа
итераций.
,
m зависит от способа
итераций.
1) Метод простой итерации (нужен спектр)
В=Е,
![]()
![]()
![]() - погрешность,
- погрешность,
![]() ,
,
![]() ,
,
![]()
![]()
коэффициент усиления
![]() - условие сходимости,
- условие сходимости,
![]()
Пусть
![]() (симметричный
оператор).
(симметричный
оператор).
2) A=LU, где
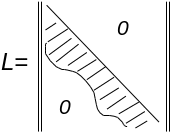 ,
,
1. Разложение А на L и U единственно
2.Разложение не меняет профиля матрицы
![]() ,
,
![]() ,
,
![]()
![]() - память,
- память,
![]() - операции.
- операции.
Обратные матрицы для U и
L вычисляются проще, чем
для всей матрицы А , т.к. они треугольные
реальное
использование ресурсов будет меньше
![]() за счет меньших коэффициентов .
за счет меньших коэффициентов .
3) Метод вложенных сечений.
![]() ,
,
![]()
В методе используется перенумерация элементов в матрице.
ЛЕКЦИЯ 12
Итерационный метод решения систем линейных алгебраических уравнений
 ,
,
где
![]() - собственные значения оператора А
- собственные значения оператора А
![]()
![]() - вариационная задача для оптимального
.
- вариационная задача для оптимального
.
![]()
![]() ,
,
![]() ,
,
![]()
Определим число итераций:
![]()
![]() - конечная погрешность решения
- конечная погрешность решения
![]() ,
,
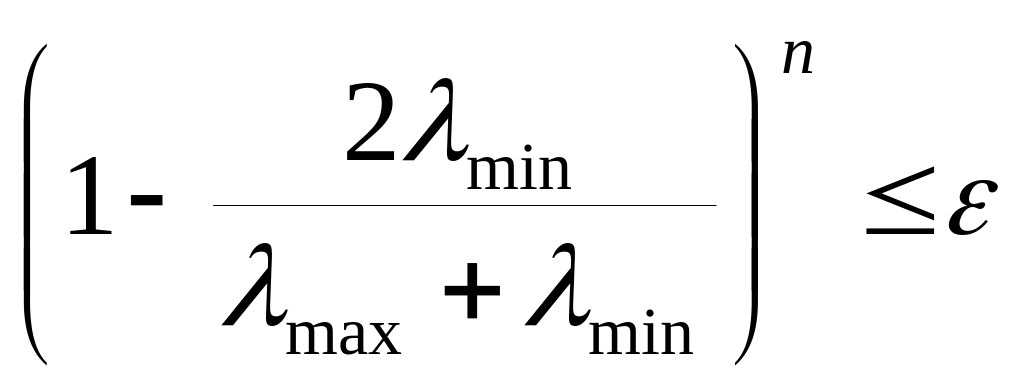 ,
,
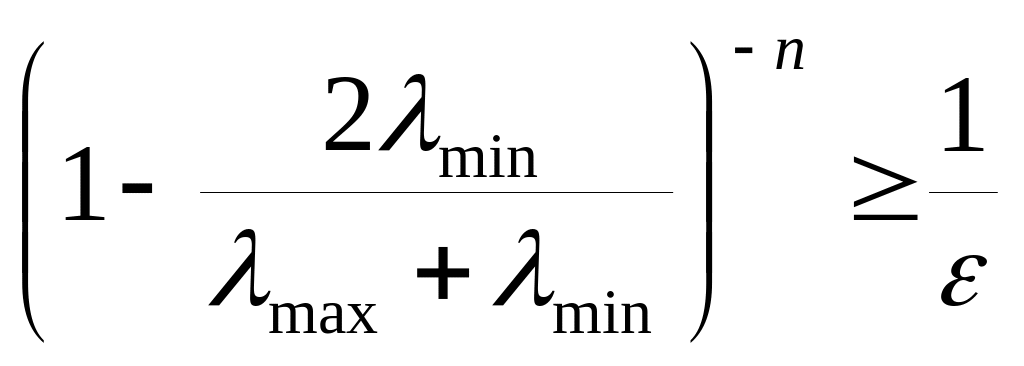
При
![]() :
:
![]()
![]()
![]() ,
,
![]()
2)
,
![]()
![]()
![]()
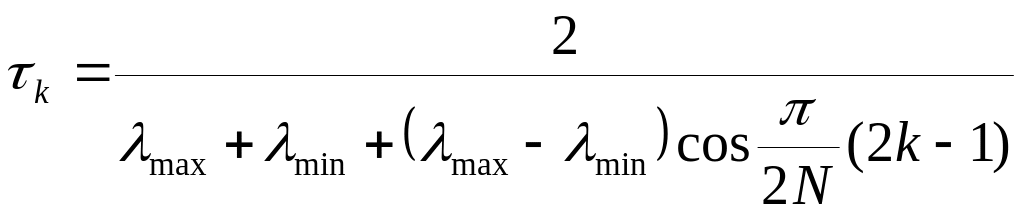
Ресурсы компьютера:
![]() - число операций (
итераций,
операций
умножения на каждой итерации –
- число операций (
итераций,
операций
умножения на каждой итерации –
перемножение
![]() )
)
![]() - объем памяти.
- объем памяти.
3)Вариационный метод нахождения в процедуре итерации
(спектр А не нужен)
,
![]() - невязка
- невязка
![]()
![]() ,
,
![]()
![]()
![]()
![]() :
:
![]() ,
,
![]() -
принцип минимальных невязок
-
принцип минимальных невязок
4) Метод переменных направлений (с переобуславливателем)
Это наиболее эффективный метод.
![]()
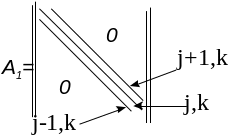

![]() ,
,
![]()
![]() (1)
(1)
Перенумеруем элементы
![]() :
:

![]() (2)
(2)
(1)
![]()
:
![]()
![]()
(*)
![]() ,
,
![]() - условие сходимости.
- условие сходимости.
![]() ,
,
,
,
