Лекция 1
Явная схема:
,
где D- дифференциальный
оператор
,
Неявная схема:
Линейная задача:
;
j=1,N;
k=1,M
-
векторная запись.
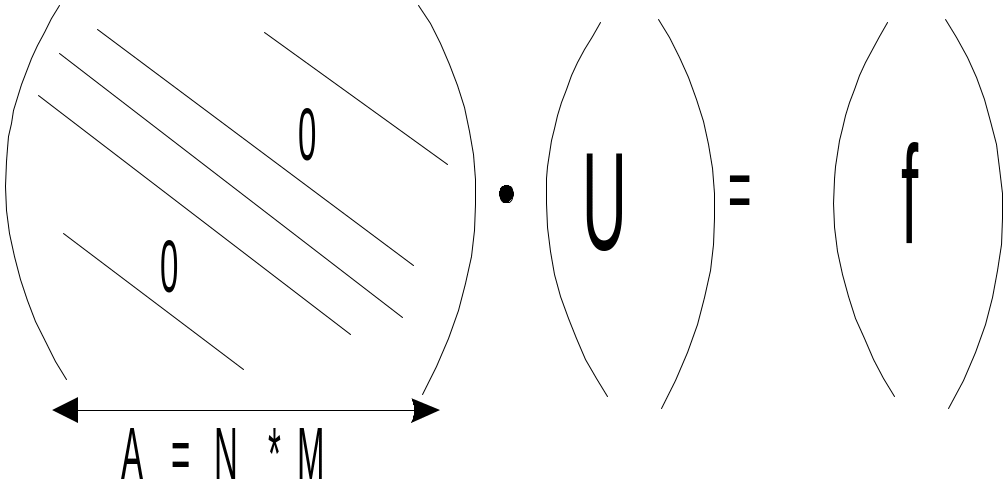
Лекция 2 Визуализация течений. Компьютерная графика.
Vertex= точка (x,y,z) или узел.
Лекция 3 Постановка задачи.
Система уравнений Эйлера:
,
-
уравнение состояния,
=
(,
u,
v,
e)T,
Векторы-потоки:
=
(u,
u2+p,
uv,
uH)T,
=
(v,
uv,
v2+p,
, vH)T
где
-
внутренняя энергия на единицу объема,
-
полная энтальпия.
Безразмерные переменные:
V,
p,
T,
,
,
,
,
,
,
-
уравнение состояния в безразмерных
переменных.
Граничные условия:
-
условие непротекания
,
М<1,
,
Типы уравнений в частных производных:
1) Эллиптические (
)
- возмущения распространяются с
-й скоростью
во всех направлениях.
2) Гиперболические (
)
- возмущения распространяются с конечной
скоростью в определенном направлении
(уравнения переноса).
3) Параболические (
)
- вырожденная координата.
,
T,
T
;
,
,
-
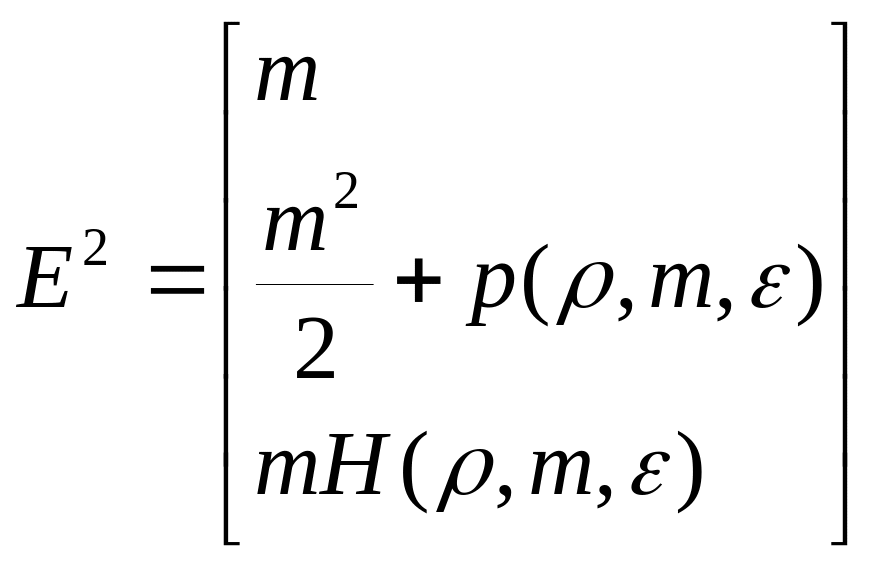матрица Якоби,
,
,
действительное гиперболический тип,
комплексное эллиптический тип,
=0 параболический тип.
Собственные числа уравнений Эйлера:
-
действительные
уравнения Эйлера гиперболические
относительно времени.
Собственные векторы:
Пусть
(*) - уравнение переноса,
-
инварианты Римана, сохраняются вдоль
характеристики.
существуют, когда течение изэнтропическое,
т.е. при
Если течение неизэнтропическое, то уравнение (*) можно использовать как приближение.
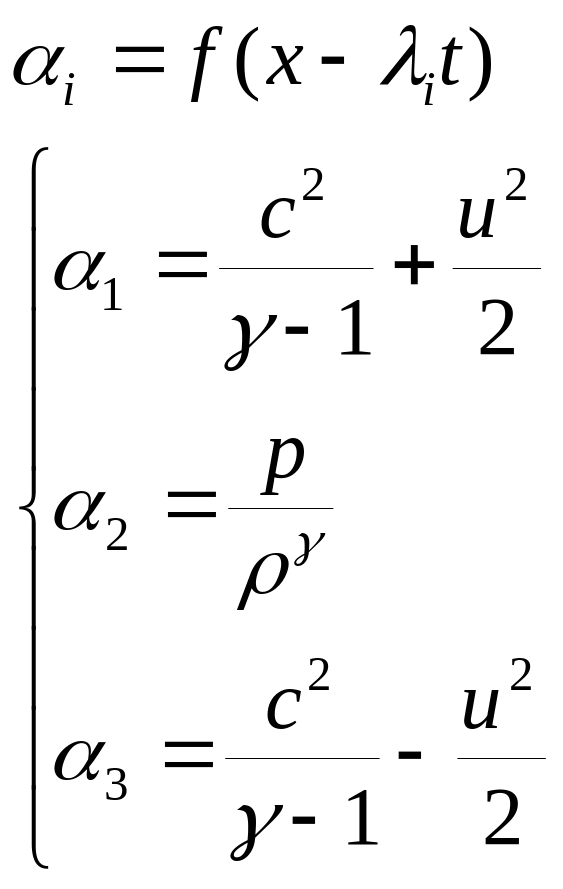
- конечная скорость распространения
возмущения.
Пример: сколько граничных условий (ГУ) надо поставить для уравнений Эйлера?
На границе х=а надо поставить 2 ГУ, т.к. 2 возмущения идут внутрь области:
- возмущение внутрь области
- возмущение внутрь области
- возмущение наружу.
На границе х=b надо
поставить 3 ГУ, т.к.
-
возмущения внутрь области.
2. Стационарный случай.
,
Т
,
,
,
=B
– невырожденный оператор
-
собственные значения.
При
все действительные
уравнения имеют
гиперболический тип,
при
(дозвук)
уравнения эллиптического типа.
Таким образом, уравнения Эйлера имеют смешанный тип. Они гиперболичны по времени, гиперболичны по пространству на сверхзвуке и эллиптичны по пространству на дозвуке.
Переход в криволинейные координаты
,
,
-
Якобиан преобразования.
Покажем, что
действительно является эквивалентом
уравнений Эйлера в прямоугольных
декартовых координатах
,
;
(1)
Численная аппроксимация
Уравнение численного интегро-аппроксимационного метода, используемого в численном решении уравнений Эйлера:
(2)
Если в уравнении (2) производные
вычислять аналитически, то получим
точность
.
При численном вычислении получим уравнение:
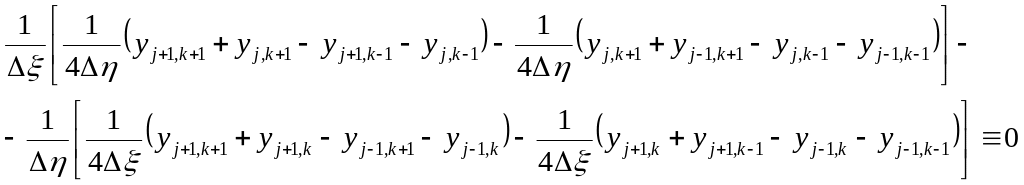
Т.е. получаем нулевую погрешность.
ЛЕКЦИЯ 4 Уравнения Навье-Стокса
;
-
уравнение состояния;
тензор
напряжений
теплопроводность вязкая диссипация
В несжимаемом случае уравнения имеют вид:
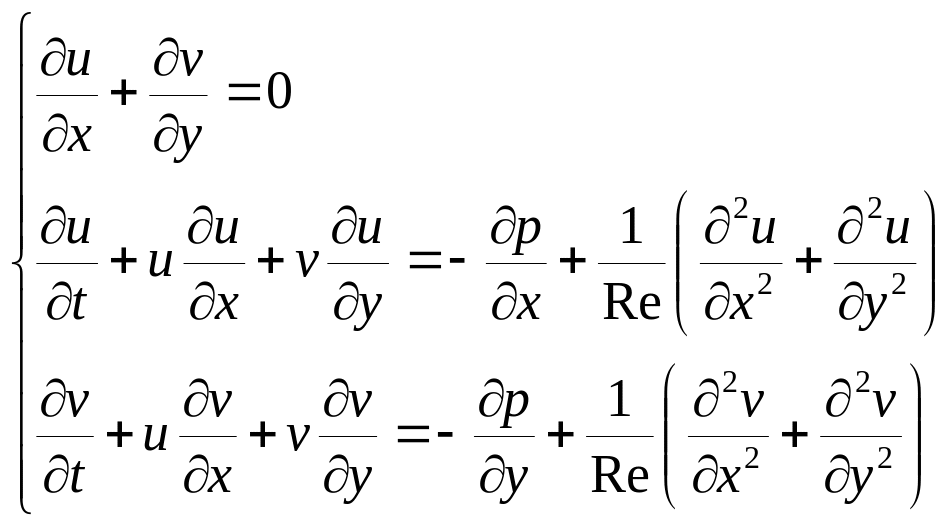
Относительно старших производных уравнения Навье-Стокса (НС) являются эллиптическими (есть лапласиан). Решения эллиптических уравнений всюду гладкие, но существуют ударные волны, в которых изменение параметров течения происходит в очень тонких областях при численном решении получим разрывы.
В уравнениях НС присутствуют и элементы гиперболического типа.
Граничные условия:
РИСУНОК
На поверхности тела:
Условие прилипания -
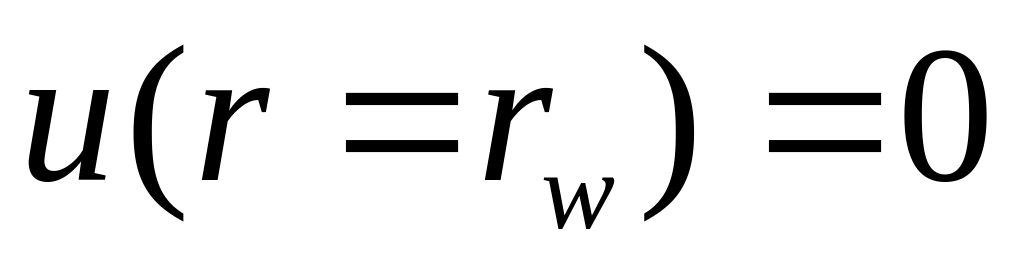
Условие непротекания -
Условие изотермической поверхности -
(
)
Условие адиабатической поверхности -
На внешней границе области ставятся ГУ из уравнений Эйлера (пренебрегаем вязкостью).
На боковых границах в системе координат () условия одинаковые, т.е. периодические.
Уравнения пограничного слоя Прандтля для несжимаемого газа:
Это уравнения параболического типа.
связанная с телом система координат.
Уравнения Прандтля не замкнуты, для их
решения необходимо знать функции
.
В параболических уравнениях возмущения распространяются строго вниз по потоку уравнения Прандтля решаются маршевым методом.