5.1 Для замкнутой системы:
Подставляя данные в (33), (34) получим следующие результаты:
,
.
5.2 Для разомкнутой системы:
,
т.к.
,
где
-
коэффициент
обратной связи,
-
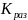коэффициент разомкнутой системы.
6. Проведение д-разбиения по коэффициенту усиления системы. Построение годографа Михайлова. Определение критического коэффициента усиления и сравнение с коэффициентом усиления, найденным в п.4
6.1 Проведение д-разбиения по коэффициенту усиления системы.
Запишем передаточную функцию разомкнутой системы:
Перед тем как начать Д- разбиение, произведем замену в передаточной функции разомкнутой системы. А именно:
.
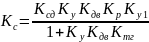После данных замен передаточная функция разомкнутой системы примет следующий вид:
.
Запишем
характеристический полином для Д-
разбиения относительно коэффициента
:
(36)
Выразив
,
раскрывая
скобки, получим следующее соотношение:
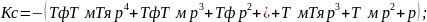(37)
Заменив в выражении (36) p на jω, получим следующие соотношение:
.
(38)
После раскрытия скобок в выражении (38) и выделения действительной и мнимой части, получим следующие соотношения для действительной и мнимой части соответственно.
U(ω)=
(39)
V(ω)=
(40)
Рассчитаем
по представленной формуле;
.
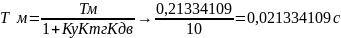(41)
Далее, при помощи программы Mathcad, при ω=0,10..1000, в соответствии с уравнениями (39) и (40), было построено в плоскости U(ω), V(ω) Д- разбиение, которое приведено на рис 5 и 5.1
6.2 Построение годографа Михайлова. Определение критического коэффициента усиления и сравнение с коэффициентом усиления, найденным в п.4
Согласно критерию
Михайлова для устойчивости динамической
системы необходимо и достаточно, чтобы
при изменениях ω от 0 до
кривая, описываемая концом вектора
характеристического
полинома Д
,
проходила против часовой стрелки через
n
квадрантов, где n
порядок характеристического уравнения.
Запишем характеристический полином для годографа Михайлова:
(42)
берется из
предполагаемой устойчивой I
области Д-разбиения. Так как граница I
области на Д-разбиении равна 104,77 1/с-
критическому
коэффициенту усиления,
то для определении области устойчивости
и построении годографа
Михайлова возьмем значение
.
После выбора
,
уравнение (42)
примет следующий вид:
(43)
Раскрыв скобки и
применив преобразование p=
ω
в выражении (43), получим следующие
соотношение:
.
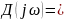
(44)
Произведем выделение действительной и мнимой части из уравнения (44) и получим следующие соотношения для действительной и мнимой части соответственно.
U(ω)=
,
(45)
V(ω)=
.
(46)
Далее, при помощи программы Mathcad, при ω=0,10..1000 в соответствии с уравнениями (45) и (46), рассчитаны U(ω), V(ω), приведенные в таблице 2, и схематично был построен годограф Михайлова, который приведен на рис 6.
Теперь по критерию
Михайлова можно сделать вывод об
устойчивости области I
Д-разбиения.
Так как годограф Михайлова начинается
на положительной вещественной полуоси,
вращается строго против часовой стрелки,
обходя все 4 квадранта, уходит в четвертом
квадранте по оси действительной части
в +
,
а по оси мнимой составлявшей в -
,
т.к. при
больших значений частот знак мнимой
части остается отрицательным, знак
действительной части остается
положительным и не пересекает начало
координат, система с коэффициентом
системы
= 50 1/с
I
области. Значит, область I
является областью устойчивости.