
- •1. Вывести необходимые уравнения движения, определить численные значение постоянных времени и коэффициентов усиления
- •2. Построение структурной схемы с указанием передаточных функции звеньев.
- •3. Определение передаточной функции замкнутой системы для регулируемой координаты по команде и по возмущению; для рассогласования-по команде и по возмущению
- •4. Определение коэффициента усиления системы и коэффициента усиления электронного усилителя по заданным условиям точности в установившемся режиме.
- •5.1 Для замкнутой системы:
- •5.2 Для разомкнутой системы:
- •6. Проведение д-разбиения по коэффициенту усиления системы. Построение годографа Михайлова. Определение критического коэффициента усиления и сравнение с коэффициентом усиления, найденным в п.4
- •6.1 Проведение д-разбиения по коэффициенту усиления системы.
- •6.2 Построение годографа Михайлова. Определение критического коэффициента усиления и сравнение с коэффициентом усиления, найденным в п.4
- •7 Построение лах (Логарифмической амплитудной характеристики) и лфх (Логарифмической фазовой характеристики)
- •1. Находим частоты сопряжения асимптот и . И значение .
- •2. Разметка системы координат.
- •4. Построение лфх.
- •5. Нахождение передаточной функции корректирующего звена.
- •6. Определение параметров последовательного корректирующего звена
- •9. Синтез пассивного корректирующего устройства
- •10. Заключение
КАЗАНСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. А.Н.Туполева
ИНСТИТУТ АВТОМАТИКИ И ЭЛЕКТРОННОГО ПРИБОРОСТРОЕНИЯ
КАФЕДРА «АВТОМАТИКИ И УПРАВЛЕНИЯ»
РАСЧЕТНО-ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
К КУРСОВОЙ РАБОТЕ
ПО ДИСЦИПЛИНЕ «МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ОПТИКО–ЭЛЕКТРОННЫХ СИСТЕМ»
по теме «Следящая система»
(Вариант Q444)
ПРОЕКТ ПРИНЯТ ПРОЕКТАНТ СТУДЕНТ
С ОЦЕНКОЙ ГР. 3337
Саркисян С. Г.
(подпись, дата) (Ф.И.О.)
ПРЕПОДАВАТЕЛЬ ПРОФЕСОР
Карпов А. И. (подпись, дата) (Ф.И.О.)
КАЗАНЬ 2016
Оглавление.
Расчет следящей системы.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Вывести необходимые уравнения движения, определить численные значение постоянных времени и коэффициентов усиления
Рис 1. Схема следящей системы
Условные обозначения, используемые на схеме.
 - Сумматор.
- Сумматор.
ФД- фазовый детектор.
Ф- фильтр.
У- усилитель.
Дв- двигатель.
Р- редуктор.
Т- объект управления.
ТГ- тахогенератор.
Uф –напряжение фильтра.
αвх – входное значение угла.
αвых – выходное значение угла.
ε – рассогласование.
Uтг - напряжение на тахогенераторе.
ΔU - разности напряжений на фильтре и на тахогенераторе.
U - напряжение после усилителя
α–угол поворота выходного вала
Исходные данные:
Jн = 0.2 кг*м2 – момент инерции нагрузки
P = 50 Вт – мощность двигателя
Uном =110 В – номинальное напряжение
i ном = 0.65 А – номинальный ток якоря
R = 20.5 Ом – сопротивление якоря
Lя = 0.115 Гн – индуктивность якоря
Jя = 0.7*10-4 кг*м2 – момент индукции якоря
n = 3000 об/мин – скорость вращения
Mв = 6.4 H*м – возмущающий момент
Ктг
= 0.04
 – крутизна статической характеристики
– крутизна статической характеристики
Кр = 0.02 – передаточный коэффициент редуктора
Тф = 0.005 с – постоянная времени фильтра
 = 10 В/рад - коэффициент
сельсин датчика
= 10 В/рад - коэффициент
сельсин датчика
i = 50 – коэффициент редукции
Показатели качества системы:
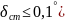 -
статическая ошибка
-
статическая ошибка
 – скоростная
ошибка
– скоростная
ошибка
 – время регулирования
– время регулирования
 - динамическая
ошибка
- динамическая
ошибка
Уравнения следящей системы:
1.Уравнение напряжения фильтра
Uф
= ε
, (1)
ε
, (1)
где: Uф –напряжение фильтра,
 -
коэффициент сельсин датчика,
-
коэффициент сельсин датчика,
Тф – постоянная времени фильтра.
2 Уравнение рассогласования
ε = αвх- αвых , (2)
где: αвх – входное значение угла,
αвых – выходное значение угла,
ε – рассогласование.
3 Уравнение разности напряжений на фильтре и на тахогенераторе
ΔU = Uф – Uтг, (3)
где: Uф – напряжение на фильтре,
Uтг - напряжение на тахогенераторе,
ΔU - разности напряжений на фильтре и на тахогенераторе.
4 Уравнение напряжения после усилителя
U = КуΔU, (4)
где: U - напряжение после усилителя,
Ку – коэффициент усилителя.
5 Уравнение двигателя.
Составим два уравнения для двигателя. Первое уравнение получено из второго закона Кирхгофа для цепи якоря:
 ,
(5)
,
(5)
здесь Lя – индуктивность якоря, Rя – сопротивление якоря, iя – сила тока якоря, α– угол поворота выходного вала, Се − коэффициент противо ЭДС равный
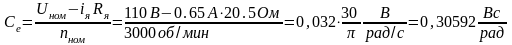 .
.
Второе уравнение представляет собой закон равновесия моментов на валу двигателя:
Jпр
 Mвпр
=Cмiя
,
(6)
Mвпр
=Cмiя
,
(6)
где Jпр – приведенный момент инерции,
Jпр=
(Jдв
+ Jн/i2)=0,7* ,
кг* м2+(0,2,
кг*
м2
/502)=0,00078
кг* м2,
(7)
,
кг* м2+(0,2,
кг*
м2
/502)=0,00078
кг* м2,
(7)
Jдв , Jн – моменты инерции двигателя и нагрузки соответственно,
Мвпр– приведенный момент.
Очевидно, что
 должен быть больше Мвпр.
должен быть больше Мвпр.
Условие 1:

 ,
(8)
,
(8)
Мвпр =MвКр =6.4*0.02= 0.128 H*м. (9)
Из уравнений (8) и (9) видно, что условие 1 выполняется, а значит редуктор с таким передаточным коэффициентом подходит.
Условие 2:
 ,
,
 .
(10)
.
(10)
Из уравнения (10) видно, что условие 2 выполняется, а следовательно использование привода, с такими параметрами возможно.
В уравнении (6) См − коэффициент момента равен:
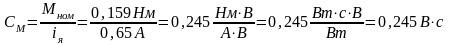 . (11)
. (11)
Преобразуем систему уравнений (5) − (6), используя оператор
 :
:
 (12)
(12)
Перепишем второе уравнение системы (12):
 .
(13)
.
(13)
В
уравнении (13)
 =
0,0056 с ,
=
0,0056 с ,
где
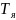 -
постоянная времени якоря.
-
постоянная времени якоря.
Из уравнения (13) имеем:
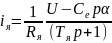 .
(14)
.
(14)
Подставляя (14) в первое уравнение системы (12) получаем:
 ,
(15)
,
(15)

 ;
;
 ;
;
(
 (16)
(16)
Перепишем уравнение (16) обозначив:
 ;
;




 − электромеханическая
постоянная двигателя;
− электромеханическая
постоянная двигателя;
 − коэффициент
усиления двигателя равен:
− коэффициент
усиления двигателя равен:
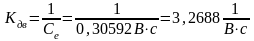 ;
(17)
;
(17)
 −
коэффициент
усиления по возмущению;
−
коэффициент
усиления по возмущению;
 (18)
(18)
И перепишем уранение (16) :
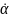 =
= . (19)
. (19)
Обозначим:


Тогда уравнение двигателя запишется следующим образом:
 .
(20)
.
(20)
Уравнение напряжения тахогенератора:
Uтг=
Ктг
=
Ктг . (21)
. (21)
Уравнение выходного значения угла:
αвых= Крα . (22)

 .
Сравнение рассогласования для
регулируемой и нерегулируемой систем
при подаче на вход команды с постоянной
скоростью 1 рад/с.
.
Сравнение рассогласования для
регулируемой и нерегулируемой систем
при подаче на вход команды с постоянной
скоростью 1 рад/с. ,
где
,
где
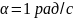 .
.