Приклад розв’язання завдання
Для сталевої балки виконати проектувальний розрахунок і підібрати переріз в 3-х варіантах: коло, прямокутник з співвідношенням сторін h/b = 2 і двотавр. Зробити оцінку економічності перерізів. Зробити повну перевірку міцності двотаврової балки. Границя текучості матеріалу балки σт = 240 МПа, а коефіцієнт запасу міцності [nт] = 1,5.
Таблиця 5
Необхідні для розрахунку дані
P, кН |
M, кН.м |
q, кН/м |
a, м |
c, м |
d, м |
h/b |
σт, МПа |
[nт] |
20 |
25 |
10 |
2 |
2 |
1 |
2 |
240 |
1,5 |
1. Розрахункова частина.
1.1. Визначення величини і напрямку опорних реакцій балки.
Визначаємо реакції опор RА і RВ з рівнянь рівноваги:
∑MА = 0: – q · a · a/2 + P · a + M + RВ · (a + c + d) = 0;
∑Mв = 0; M – P · (c + d) + q · a · (c + d + a/2) – RА · (a + c + d) = 0;
Перевірка знайдених реакцій:
∑y = RA – q · a + P + RВ = 9 – 10 · 2 + 20 + (–9) = 0.
Модулі реакцій знайдені вірно, але напрямок реакції RВ слід змінити на протилежний. Реакція RВ спрямована вниз.
1.2. Побудова епюр згинальних моментів і поперечних сил на кожній дільниці балки і перевірка правильності побудови цих епюр.
Зробимо ескіз балки у довільно обраному масштабі і прикладемо до неї задане навантаження і правильно визначені реакції.
Розіб’ємо балку на ділянки і визначимо згинальні моменти і поперечні сили у довільних перерізах цих ділянок.
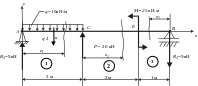
Балка має 3 ділянки:
1 – АС;
2 – СЕ;
3 – ВЕ.
1 ділянка: 0 ≤ z1 ≤ 2 м. Початок координат у т. А. Згинальний момент у довільному перерізі ділянки:
Mz1 = RA · z1 – q · z1 · z1/2 = 9 z1 – 10z12/2;
z1 = 0; Mz1 = 0; z1 = 2 м; MС = 18 – 20 = – 2 кН.м;
z1 = 1 м; MО = 9 – 5 = 4 кН.м.
Поперечна сила Qу у довільному перерізі:
Qу = RA – q · z1 = 9 – 10z1;
z1 = 0; QА = 9 кН; z1 = 2 м; QС = 9 – 20 = – 11 кН;
z1 = 1 м; QО = 9 – 10 = – 1 кН.
Знайдемо, при якому значенні z1 поперечна сила дорівнює нулю: Qу = 0.
0 = 9 – 10 z1; звідки z1 = 0,9 м. Згинальний момент при z1 = 0,9 м на ділянці АС.
Mz max = 9z1 – 10 z12/2 = 9 · 0,9 – 10 · 0,92/2 = 8,1 – 4,05 = 5,05 кН·м
2 ділянка: 0 ≤ z2 ≤ 2 м. Початок координат у точці С.
z2
= 0; 
= 18 – 20 = – 2 кН.м;
z2 = 2м; = 36 – 60 + 40 = 16 кН.м;
Поперечна сила Q:
Qz = RA – q · 2 + P = 9 – 20 + 20 = 9 кН.
3 дільниця: 0 ≤ z3 ≤ 1 м. Початок координат у т. В.
= – RB
· z3
= – 9 · z3;
z3 = 0; = 0; z3 = 1м; = – 9 кН.м.
Поперечна сила:
Qz3 = RВ = 9 кН.
Результати обчислень представимо у вигляді таблиці 6.
Таблиця 6
Розрахункові значення Mz і Qz
Дільниця |
Z, м |
Mz, кН·м |
Qz, кН |
||
АС |
0 ≤ Z1 ≤ 2 |
0 |
–2 |
9 |
–11 |
СЕ |
0 ≤ Z2 ≤ 2 |
–2 |
16 |
9 |
9 |
ЕВ |
0 ≤ Z3 ≤ 1 |
0 |
–9 |
9 |
9 |
Будуємо епюри згинальних моментів і поперечних сил у довільно обраному масштабі (рис. 1).
Рисунок 1