2.3 Задача № 3. Работа со списками

Пример решения задачи

Для демонстрации возможностей работы со списками в электронной таблице MS Excel необходимо подготовить примеры и разместить их на листе рабочей книги.

Например, “Автокаталог”. ВНИМАНИЕ! Вы должны придумать свой оригинальный пример и подготовить текст, описывающий технологию работы с таблицами в соответствии в Вашим примером. Пример, приведенный в методических указаниях, не может быть использован при выполнении контрольной работы.

На рисунках 4-10 показаны фрагменты таблиц списка (база данных): на тему «Автокаталог», размещенных на листе "Задача 3" рабочей книги Excel.

Рисунок 4 – Таблица с исходным списком

Рисунок 5 – Таблица после сортировки

Рисунок 6 – Использование фильтра

Рисунок 7 – Использование расширенного фильтра

Рисунок 8 – Подведение итогов и создание структуры данных

Рисунок 9 – Сводная таблица

Рисунок 10 – Диаграмма

В пояснительной записке необходимо описать технологию работы со списками в электронной таблице MS Excel (создания списка, сортировки и фильтрации данных, подведения промежуточных и общих итогов, создания структуры данных, создания сводной таблицы и диаграммы), включив в текст описания названия заголовков полей списка и рисунки экранных форм рабочего окна MS Excel с примерами подготовленных таблиц. Фрагмент описания технологии работы со списками в MS Excel приведен ниже.

Предметная область списка (база данных): “Автокаталог”.

Список представляет собой набор строк таблицы, содержащий связанные (по смыслу) данные. Список может выступать в качестве базы данных, если соблюдаются следующие условия: строки таблицы выступают в качестве записей, столбцы таблицы являются полями, заголовки столбцов, то есть первая строка списка, становятся именами полей базы данных [1].

В строке 4 листа рабочей книги Excel "Задача 3" введем заголовки полей списка (базы данных): «Номер»; «Марка»; «Цвет»; «Пробег»; «Год выпуска»; «Объем двигателя»; «Стоимость, тыс. руб.». Заполним таблицу данными как показано на рисунке 11. Всего заполнено 20 строк списка.

Рисунок 11 – Список (база данных) «Автокаталог»

Сортировка.

Отсортировать список можно в алфавитном, числовом и хронологическом порядке. При этом можно задать возрастающий, убывающий и пользовательский порядок сортировки [2].

Если был задан возрастающий порядок сортировки, все числа столбца сортируются в порядке от наименьшего отрицательного числа к наибольшему положительному; значения даты и времени располагаются в хронологическом порядке от самого раннего к самому позднему; текстовые данные сортируются по алфавиту, при этом в начале списка окажутся заданные в качестве текста числовые значения; список логических значений будет начинаться со значения ЛОЖЬ и заканчиваться значением ИСТИНА; а значения ошибок будут отсортированы в том порядке, в котором они были обнаружены. При возрастающем порядке сортировки пустые ячейки будут сдвинуты в конец списка.

При убывающем порядке сортировки все числа столбца сортируются от наибольшего положительного к наименьшему отрицательному; значения даты и времени располагаются в порядке от самого позднего к самому раннему; текстовые данные сортируются в обратном алфавитном порядке; список логических значений будет начинаться со значения ИСТИНА и заканчиваться значением ЛОЖЬ. Пустые ячейки будут сдвинуты в конец списка.

При применении пользовательского списка сортировки значения будут отсортированы в соответствии с четко зафиксированной последовательностью заданного списка [1].

Отсортируем список “Автокаталог” по двум уровням - сначала по столбцу «Год выпуска», затем по столбцу «Стоимость». Сортировку выполняем по возрастанию. Для сортировки используем меню: «Данные\Сортировка». Окно выбора параметров сортировки показано на рисунке 12.

Рисунок 12 – Сортировка данных

Результат выполненной сортировки списка "Автокаталог" показан на рисунке 13.

Рисунок 13 – Результат сортировки

Аналогично должны быть описаны технологии выполнения:

• − фильтрации (автофильтр и расширенный фильтр) (рисунки 6 и 7);

• − подведения промежуточных и общих итогов (рисунок 8);

• − создания структуры данных (рисунок 8);

• − создания сводной таблицы (рисунок 9); − создания диаграммы (рисунок 10).

Задача 4. Система линейных уравнений

Задание:

• Найти решение системы линейных уравнений методом обратной матрицы.

• Записать систему линейных уравнений в «классическом виде»

• Ввести матрицу коэффициентов при неизвестных и правые части.

• Решить систему линейных уравнений методом «обратной матрицы».

Решение.

Дана система линейных уравнений:

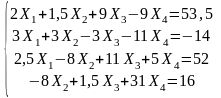
На новом листе (Переименовать «Задание 4») записать матрицу коэффициентов системы уравнений (размерность 4×4), и матрицу правых частей (размерность 4×1). Отсутствующие коэффициенты при неизвестных равны нулю.

При помощи функции МОБР(A2:D5) вычислить матрицу, обратную матрице коэффициентов уравнений¹.

При помощи функции МУМНОЖ выполняется умножение обратной матрицы на матрицу правых частей системы уравнений. Результат операции – матрица размерностью 4×1 является решением системы линейных уравнений.

Решение системы уравнений:

Задача №5 Решение нелинейного уравнения

Создать новый лист «Задание 5».

Найти один из корней нелинейного уравнения. Выполнение индивидуального задания должно состоять из следующих пунктов:

Отделение корня графическим методом - необходимо построить график функции, приведённой в задании, и найти хотя бы один отрезок, где он пересекает ось X, это будет приблизительное значение корня. Если ни одного отрезка найти не удалось, нужно изменить область построения.

Уточнение корня - используя два специальных средства: «Подбор параметра» и «Поиск решения», сузить найденный отрезок до 0,001. Это и будет значение корня с точностью до 0,001.

Простейшим случаем задачи оптимизации является определение корня нелинейного уравнения. Уравнение f (х) = 0 будет нелинейным, если в его правой части присутствует неизвестная в степени, отличной от 1, или имеются трансцендентные функции sin(x), Ln(x) и т.д. Для некоторых уравнений существуют методы, позволяющие получить точное решение (например, квадратное уравнение). Однако большинство из них не имеет точного аналитического решения.

Чаще всего нелинейное уравнение имеет несколько корней, поэтому его приближённое решение состоит из двух этапов.

На первом этапе производится грубый подбор или отделение корня, то есть находятся все или хотя бы один отрезок, на котором есть корень. Для этого следует просчитать таблицу значений функции на произвольно выбранном интервале и построить график. Напомним, что корень - это значение х, при котором левая часть уравнения равна 0. На графике это отрезок, на котором функция пересекает ось X, соответственно в таблице -отрезок на котором функция меняет знак. Если на выбранном интервале корней не оказалось, следует поискать их на другом отрезке, просто изменив значения в столбце аргументов.

На втором этапе отделённый корень определяется с заданной точностью. Для этого можно использовать средство «Подбор параметра» (ДАННЫЕ – АНАЛИЗ «ЧТО ЕСЛИ…» _ «ПОДБОР ПАРАМЕТРА». Для этого нужно заполнить на рабочем листе две ячейки: в одной записать значение аргумента, а во второй формулу для расчета функции, являющейся левой частью уравнения. Эти ячейки можно просто скопировать из таблицы. В качестве начального значения аргумента X следует выбрать левую границу отрезка, на котором обнаружен корень. С таким же успехом можно для этой цели можно использовать средство «Поиск решения» (ДАННЫЕ – ПОИСК РЕШЕНИЯ). Поскольку «Поиск решения» позволяет задавать ограничения, можно легко найти все отделенные корни, задавая в качестве ограничений границы отрезков, на которых обнаружены корни.

Задание:

Найти один из корней нелинейного уравнения:

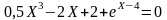
Решение

Порядок действий:

• Отделить корни графическим методом, для этого построить график функции 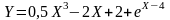и найти хотя бы одно пересечение графика с осью X. Отрезок, на котором график функции пересекает ось X, является базовым для дальнейшего уточнения корня.

• Для уточнения значения корня использованы средства «Подбор параметра» и «Поиск решения». В обоих случаях в качестве начального значения X выбираем левую границу отрезка, на котором есть корень.

Как видно из таблицы и графика функции имеет корень, на отрезке [-3;-2]. Для уточнения корня используем средства «Подбор параметра» и «Поиск решения». В обоих случаях значения корня X=-2,383.

Настройка окон «Подбор параметра» и «Поиск решения».

На рисунке показан пример заполнения окна «Поиск решения» и дополнительной формы «Добавление ограничения» при решении задачи нахождения корней нелинейного уравнения.