Лабораторная работа№13. Определение теплопроводности материалов при нестационарном режиме

Кайгородова о.А..Комляшов р.Б.

Наука о теплообмене изучает самопроизвольные необратимые процессы распространения теплоты в пространстве.

Перенос теплоты может осуществляться тремя основными способами: теплопроводностью, конвекцией и тепловым излучением.

Теплопроводностью называется молекулярный процесс распространения теплоты при непосредственном контакте между телами или частями тел с различной температурой. В чистом виде этот процесс возможен лишь в однородных твердых телах.В общем случае процесс переноса теплоты теплопроводностью сопровождается изменением температуры как в пространстве, так и во времени. Совокупность значений температуры во всех точках изучаемого тела или пространства для каждого момента времени определяет температурное поле.

Процессы теплопроводности, в которых поле температур внутри тел меняется не только в пространстве, но и по времени, называются нестационарными (нестационарная теплопроводность). Нестационарность таких процессов, прежде всего, связана с нагревом и охлаждением тел.

Любой процесс нагрева и охлаждения можно разделить на 3 стадии.

1. Первая охватывает начало процесса и характеризуется постепенным распространением температурных возмущений, захватывающих все новые и новые участки тела. Скорость изменения температуры в отдельных точках тела может различной и сильно зависит от начального распределения температур в теле и удаленности этих точек от источника нагрева или охлаждения. Поэтому первая стадия процесса называется неупорядоченным режимом.

2.С течением времени влияние начальных неравномерностей сглаживается, и относительная скорость изменения температуры во всех точках тела становится постоянной. Наступает вторая стадия – режим упорядоченного процесса, который называют регулярным.

3.Затем после долгого, относительно начальной стадии, промежутка устанавливается третий режим – стационарный режим с постоянным распределением температуры в теле, не зависящим от времени.

Решения простейших задач нестационарной теплопроводности могут быть сведены к таблицам или номограммам. Однако даже в этих случаях вычисления рядов, которыми представляется точное аналитическое решение, вызывает значительные трудности, не говоря уже о телах сложной формы, изменяющихся по времени условий внешнего теплообмена и т.п. Поэтому при изучении переходных теплообменных процессов большее применение находят методы прямого численного интегрирования дифференциальных уравнений. В нашем случае речь идет о численном интегрировании дифференциального уравнения теплопроводности Фурье-Кирхгофа, имеющего вид для одномерной задачи:

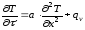, (1)

где q_v – интенсивность внутренних источников или стоков тепла,

а – коэффициент температуропроводности, который определяет скорость распространения температурных возмущений, является функцией теплоинерционных свойств веществ и зависит от их теплоемкости–Ср , плотности –  и коэффициента теплопроводности – λ.

а =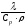 (2)

Дифференциальное уравнение Фурье описывает явление передачи теплоты теплопроводностью в самом общем виде. Чтобы применить его к конкретному случаю, необходимо задать условия однозначности, или краевые условия:

• геометрическую форму и размеры тела;

• физические параметры среды и тела;

• начальные условия (распределение температуры в теле в начальный момент времени);

• граничные условия, характеризующие взаимодействие тела с окружающей средой.

Рассмотрим один из методов численного интегрирования на примере прогрева металлического стержня длиной 50 мм с диаметром поперечного сечением 20 мм с граничными условиями первого рода, когда на концах стержня заданы постоянные температуры Т₁ и Т₂. Начальные условия задаются в виде однородного распределения температур ТхТ₂.Задается температура окружающей среды Т₀ закон теплообмена между поверхностью тела с окружающей средой. Для этого чаще всего используется закон Ньютона – Рихмана, согласно которому количество теплоты, отводимое через единицу поверхности тела в единицу времени, пропорционально разности температур поверхности тела и окружающей среды.

Согласно закону сохранения энергии количество теплоты, которое отводится с единицы поверхности в единицу времени вследствие теплоотдачи, должно равняться теплоте, подводимой к единице поверхности в единицу времени вследствие теплопроводности из внутренних объемов тела. При этом конвективные потери тепла через боковую поверхность стержня интерпретируются как внутренние стоки тепла, так что:

q_v= Т_j-Т₁ПS, (3)

где П и S – периметр и площадь поперечного сечения стержня соответственно.

Таким образом, задавая дополнительно к геометрическим, начальным и граничным условиям физические условия - плотность, теплопроводность и теплоемкость стержня, мы получаем полную математическую постановку задачи нестационарной теплопроводности при одностороннем нагреве стержня.

При численном интегрировании стержень условно разбивается на N отдельных ячеек, для каждой из которых составляется и многократно решается разностный аналог исходного дифференциального уравнения:

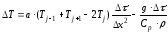(4)

Метод позволяет рассчитать поля температур и тепловых потоков внутри стержня в любой момент времени, текущие значения безразмерного времени и суммарное количество тепла, передаваемого вдоль стержня теплопроводностью.

Процесс нестационарной теплопроводности демонстрируется на установке в режимах разогрева и охлаждения (выход на установившейся режим).

Для стационарного режима с распределение температуры вдоль стержня по оси Х можно описать уравнением:

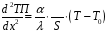(5)

где T, T₀– температура стержня и окружающей среды, С;

α – коэффициент теплоотдачи, Вт/(м² ·K);

λ– коэффициент теплопроводность материала, Вт/(м·K);

П – периметр сечения стержня, м;

S – площадь поперечного сечения, м².

Если в уравнении 5 сделать следующую замену:

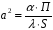(6)

то решением уравнения 5 является:

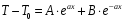(7)

Предположим, что при x=0 T=T₁, а сам стержень бесконечно длины, то проинтегрировав решение получим:

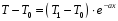(8)

откуда:

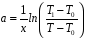(9)

В этом случае, используя соотношение 3, тепловой поток будет равен:

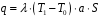(10)

Заменим a выражением 9 и получим:

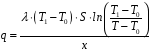(11)

Тогда, коэффициент теплопроводности можно определить из выражения:

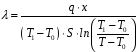(12)

где x – расстояние между термопарами, м;

q–количество теплоты отдаваемое стержню от нагревателя,Вт;

T₁–температура нагреваемого конца, С;

T₀–температура окружающей среды, С;

T–температура стержня на расстоянии х, С;

S– площадь поперечного сечения стержня, м2 .

Таким образом, учитывая, что мощность нагревателя и количество теплоты каждому стержню отдается одинаковое, то взяв за эталонный образец материал с известной теплопроводностью можно вычислить количество теплоты, отдаваемое эталонному стержню, а затем определить теплопроводность неизвестных образцов. Такой алгоритм расчета соответствует методу продольного теплового потока.

В данной работе проводится исследование нестационарной теплопроводности и определение коэффициентов теплопроводности и температуропроводности металлических стержней, выполненных из стали 20, бронзы и алюминия. Все стержни имеют одинаковые размеры: длина 50 мм, диаметр поперечного сечения 20мм за эталонный образец принят медный образец.

Физические характеристики эталонного медного образца при 20⁰С представлены в Таблице1

Таблица 1. Характеристики медного образца

Характеристика	Значение
Плотность, кг/м3	8940
Удельная теплоемкость, Дж/кг К	390
Коэффициент теплопроводности, Вт/мК	387

Задачи работы:

1. Экспериментальное и численное исследование нестационарной теплопроводности металлических тел.

2. Построение зависимостей изменения температуры от времени с использованием программы сбора данных.

3. Экспериментальное определение коэффициентов теплопроводности и температуропроводности металлов.

Описание экспериментальной установки

Используемая в эксперименте установка (рис. 1) состоит из нагревателя (4) с тепловыделяющим элементом и программно-управляемым блоком регулирования температуры (6). Исследуемые металлические стержни (1-3) полированной торцевой поверхностью прижимаются к нагревателю винтовым соединением (рис.2). В каждом образце закреплены по 2 термопары, электрические сигналы с которых выводятся на три двухканальных цифровых измерителя температур (5). При повышении заданной температуры каждый из них имеет возможность выводить сигнал для управления режимом работы нагревателя.

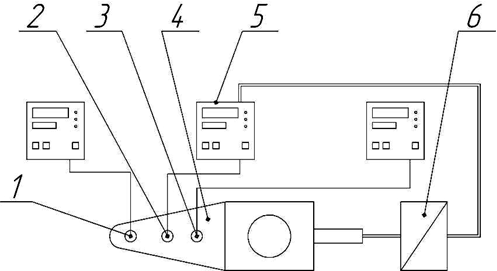
Рис.1. Схема экспериментальной установки

1-3 – стержни из исследуемых материалов (1- алюминий, 2 – латунь (бронза), 3 - нержавеющая сталь), 4 – нагреватель, 5 –двухканальные цифровые термометры для каждого образца, 6 – программно-регулируемый блок температуры нагревателя.

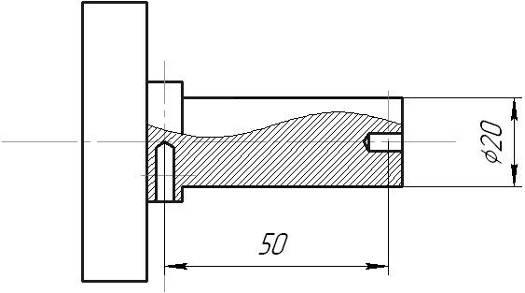
Рис.2. Крепление образцов к нагревателю

(в разрезе показаны места установки термопар Т₁ и Т₂).