33. Символ . Эквивалентность
Определение:
Говорят, что
есть 
при
,
если 
,
где
б.м. функция при
Отметим,
что если 
при
,
то в определении можно записать:
.
Примеры:
так
как
(
б.м. при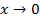 
).
,
так
как
(
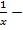б.м. при 
).
Определение:
Б.м.
и
называются эквивалентными при
,
если 
,
где
(под
подразумевается конечная точка или
).
Обозначение:
при
.
Пример:
при 
.
В
случае, когда
,
имеем
,
если .
Примеры:
При
x;
;
x;
;
;
;
;
.
Теорема:
Пусть 
Тогда
;
.
По определению эквивалентности 
,
где 
при
Тогда
.
Для
теорема доказывается аналогично. •
Предостережение: Нельзя заменять слагаемые в сумме или в разности на эквивалентные функции. Это может привести к ошибке!
Пример:
Вычислить
.
Если заменить первое слагаемое на
эквивалентную при
функцию
,
получим 0. В то время как
Теорема:
Функции
и
эквивалентны при
тогда и только тогда, когда 
Дано: 
то
есть, 
,
или
где 
б.м. при
Имеем
при
Дано:
или
.
•
34. Теорема о пределе сложной функции
Определение:
Пусть функция
имеет множество определения
и множество значений, лежащее в 
при 
Пусть
имеет множество определения 
,
тогда на множестве
определена функция 
Говорят: 
сложная
функция. Здесь 
внутренняя функция, 
внешняя функция.
По-другому:
композиция функция
и 
,
суперпозиция
и
,
обозначение –
.
Теорема
1 (о пределе сложной функции):
Пусть функция
определена в 
и
.
Пусть
непрерывна в точке
,
тогда предел
.
такое,
что 
,
для
.
Это возможно в силу непрерывности
в точке В.
Для полученного
найдем
такое, что
.
Это возможно по определению предела.
Итог:
имеем
.
•
Теорема
2 (о пределе сложной функции):
Пусть
,
,
причем 
при 
тогда
.
35. Переход к пределу в неравенствах
Теорема:
Пусть существуют
и
.
Тогда 
Рис. 20
Выберем
,
тогда
такое, что
.
(1)
Для
того же
. (2)
Возьмем
,
тогда выполняется одновременно (1) и (2)
,
т.е. мы получаем 
.
•
Следствие (лемма о сохранении знака непрерывной функции):
Пусть
функция непрерывна в точке
,
,
тогда 
,
такое что 
•
Рис. 21
36. Переход к пределу в двойном неравенстве
Теорема
1:
Пусть 
определены 
.
Пусть
,
и пусть существуют
.
Тогда
существует
.
.
(1)
Тогда такое, что
. (2)
Аналогично
.
(3)
Возьмем
.
Тогда
неравенства (1), (2), (3) выполнены
одновременно. Получаем 
.
.
•
Теорема
2:
Построим окружность радиуса 1 с центром в точке О. Пусть
Рис. 22
Тогда
.
Пусть
. Имеем 
.
Умножим
все части неравенства на 2 и разделим
на
:
. (4)
Заметим,
что все функции, входящие в неравенство
(4) – четные. Следовательно, (4) справедливо
при
.
Итак, неравенство (4) выполняется при
.
Функция 
непрерывна в точке х
= 0
.
По теореме 1 . •
Примечание:
Из теоремы 2 следует, что
х.
.