
- •Глава 1: функция. Предел. Непрерывность
- •1. Действительные числа
- •Если , то ;
- •Если , то
- •2. Некоторые обозначения
- •3. Промежутки на числовой прямой
- •4. Абсолютная величина
- •6. Ограниченное множество. Точные грани
- •7. Отображение. Функция
- •8. Последовательности
- •9. Предел последовательности
- •10. Единственность предела последовательности
- •11. Ограниченность последовательности, имеющей конечный предел
- •12. Бесконечные пределы (последовательности)
- •13. Подпоследовательности
- •14. Арифметические действия с пределами
- •15. Бесконечно малые и бесконечно большие последовательности
- •16. Связь бесконечно больших и бесконечно малых последовательностей
- •17. Свойства бесконечно малых последовательностей
- •18. Теорема Вейерштрасса
- •19. Число e
- •20. Предел функции в точке
- •26. Бесконечно малая функция
- •27. Арифметические действия с пределами
- •28. Бесконечно большие и бесконечно малые функции
- •29. Непрерывность функции
- •30. Непрерывность тригонометрических функций
- •31. Односторонние пределы
- •32. Классификация точек разрыва
- •33. Символ . Эквивалентность
- •34. Теорема о пределе сложной функции
- •35. Переход к пределу в неравенствах
- •36. Переход к пределу в двойном неравенстве
- •37. Теорема Коши о промежуточном значении непрерывной функции
- •38. Обратная функция
- •39. График обратной функции
- •40. Существование обратной функции
- •41. Непрерывность обратной функции
- •42. Непрерывность элементарных функций
- •Глава 2: производная
- •44. Определение производной
- •45. Производные основных элементарных функций
- •46. Дифференцируемая функция
- •47. Дифференцирование результатов арифметических действий с функциями
- •48. Производная обратной функции
- •49. Производная сложной функции
- •50. Таблица производных
- •51. Геометрический смысл производной
- •52. Дифференциал функции
- •53. Линеаризация функции
- •58. Теорема Ролля
- •59. Теорема Лагранжа
- •60. Теорема Коши
- •61. Производные высших порядков
- •62. Погрешность линейного приближения
- •63. Правило Лопиталя
- •64. Достаточное условие возрастая и убывания функций
- •65. Достаточное условие экстремума
- •Глава 3: формула тейлора
- •66. Параболическое приближение
- •67. Многочлен Тейлора
- •68. Формула Тейлора-Лагранжа
- •73. Достаточные условия выпуклости
- •74. Точка перегиба
- •75. Асимптоты
- •76. Построение графиков функций
- •Глава 4. Числовые ряды
- •77. Сходимость числового ряда
- •78. Свойства сходящихся рядов
- •79. Необходимое условие сходимости
- •80. Ряды с неотрицательными членами
- •81. Признак сравнения
- •82. Предельный признак сравнения
- •83. Признак Даламбера
- •84. Радикальный признак Коши
- •85. Абсолютно сходящиеся ряды
- •86. Знакочередующиеся ряды
Глава 1: функция. Предел. Непрерывность
1. Действительные числа
Действительным
числом называется бесконечная дробь
вида
![]() ,
где
,
где ![]() =0,
1, 2 … m,
… - неотрицательное число;
=0,
1, 2 … m,
… - неотрицательное число; ![]() = 0, 1, 2 … 9; n=1,
2…; – неотрицательное действительное
число.
= 0, 1, 2 … 9; n=1,
2…; – неотрицательное действительное
число.
Если хотя бы одно из чисел , то – положительное действительное число, - – отрицательное действительное число.
Множество
действительных чисел обозначается ![]() .
.
Между точками геометрической прямой и действительными числами можно установить взаимно однозначное соответствие. Числу 0 соответствует точка O, единице – точка E:
![]()
вектор
![]() принят за координатный орт. Таким
образом, каждому числу поставлена в
соответствие точка с координатой, равной
этому числу.
принят за координатный орт. Таким
образом, каждому числу поставлена в
соответствие точка с координатой, равной
этому числу.
Поэтому множество действительных чисел называют также числовой прямой или числовой осью. Сами действительные числа называются точками числовой прямой.
Расширенное множество действительных чисел – это множество действительных чисел, дополненное двумя элементами: +∞ (плюс бесконечность) и –∞ (минус бесконечность) такими, что по определению считается:
если
 ,
то –
,
то –
Если , то ;
Если , то
Расширенное
множество действительных чисел
обозначается ![]() .
.
2. Некоторые обозначения
-
Символ
Разъяснение

Для любого, для каждого, для всех

Существует, найдется
AB: A влечет за собой B, B следует из A
AB: A следует из B и B следует из A; AB: A равносильно B; A необходимо и достаточно для B; A тогда и только тогда, когда B

 – множество, состоящее из элементов
– множество, состоящее из элементов


состоит из таких элементов
 ,
которые обладают свойством
,
которые обладают свойством 
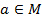
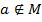
Элемент
 принадлежит множеству
,
соответственно, элемент
не принадлежит множеству
принадлежит множеству
,
соответственно, элемент
не принадлежит множеству

Пустое множество, множество, не содержащее ни одного элемента

Множество
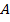 содержится в множестве
содержится в множестве 

Множество натуральных чисел
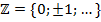
Множество целых чисел

Множество рациональных чисел

Множество действительных чисел
3. Промежутки на числовой прямой
Пусть
числа ![]()
Конечные промежутки
Интервал
![]()
![]()
Отрезок
![]()
![]()
Полуинтервалы:
![]()
![]()
![]()
![]()
Бесконечные промежутки
Интервалы:
![]()
![]()
![]()
![]()
x![]()

Полуинтервалы:
![]()
![]()
![]()
![]()
4. Абсолютная величина
Определение:
Пусть ![]()
Число
![]() называется абсолютной величиной или
модулем числа
называется абсолютной величиной или
модулем числа ![]()
Свойства модуля:
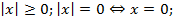
 и
и  при
при 

 ;
;;
 ;
;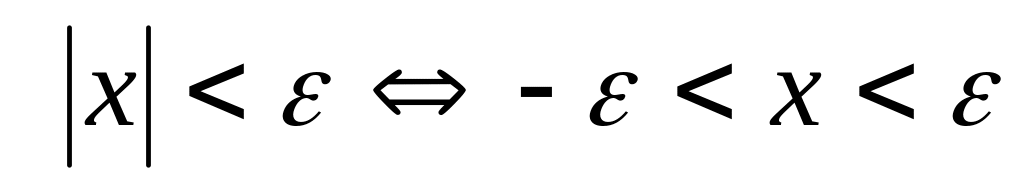
 – неравенство треугольника;
– неравенство треугольника;
5. -окрестность
Окрестностью точки называется любой интервал, содержащий эту точку.
![]()
Обозначение:
![]()
Определение:
Пусть ![]() – некоторое число. Множество
– некоторое число. Множество ![]() называется -окрестностью
точки
.
называется -окрестностью
точки
.
Геометрически:
![]()
![]()
![]()

Если
из этого множества удалить точку
,
то получится множество – проколотая
окрестность точки
– ![]()

Правая
-окрестность точки
– ![]()
![]()
Правая
проколотая ![]() -окрестность точки
–
-окрестность точки
– ![]()
![]()
Левая
-окрестность точки
– ![]()
![]()
Левая
проколотая
-окрестность точки
–
![]()
![]()
Пусть
,
множество ![]() называется
-окрестностью
плюс бесконечности,
называется
-окрестностью
плюс бесконечности,

а
множество ![]() – -окрестностью
минус бесконечности/
– -окрестностью
минус бесконечности/

