
Методичка 4816 Теор вер
.pdf
|
|
|
61 |
|
|
0 при ≤ 15, |
|
|
|
|
|
|
|
0,4 при 15< ≤16, |
|
( ) = |
|
0,5 при 16< ≤17, |
(1) |
|
|
0,8 при 17< ≤18, |
|
|
|
1 при ≥18. |
|
Построим график функции ( ).
Рис. 7.5
Ответ: а) формула (1); б) рис. 7.5.
Задачи
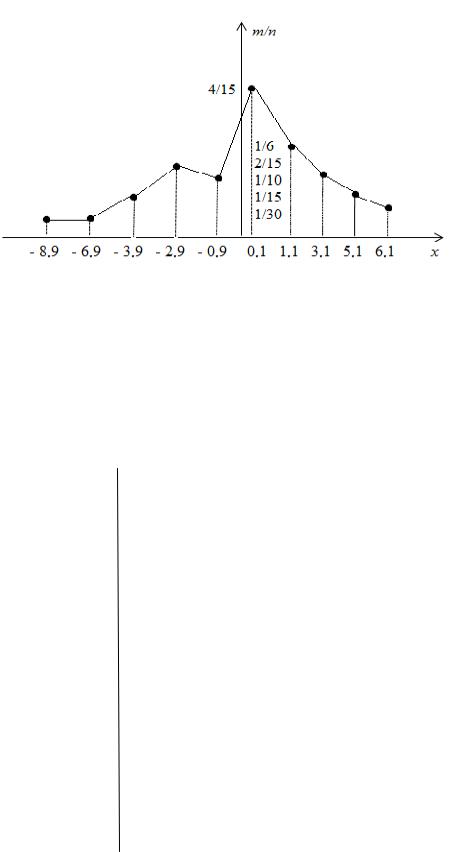
7.1. В результате испытаний получены следующие статистические значения случайной величины X:
0,9; 0,1; 2,9; 1,1; 5,1; 0,1; 6,9; 1,1; 3,9; 0,9; 5,1; 8,9; 2,9; 0,1; 1,1; 6,1; 3,1; 0,1; 1,1; 2,9;
2,9; 0,1; 3,9; 0,9; 0,1; 3,1; 0,1; 1,1; 3,1; 0,1.
Требуется: а) составить статистический ряд;
б) найти статистическую функцию распределения ( );
в) изобразить полигон относительных частот.
7.2. В результате испытаний получены следующие статистические значения случайной величины X:
1,36; 1,37; 1,35; 1,31; 1,34; 1,36; 1,38; 1,35; 1,39; 1,40;
62
1,33; 1,34; 1,36; 1,35; 1,37; 1,41; 1,36; 1,34; 1,39; 1,36; 1,35; 1,37; 1,38; 1,40; 1,37; 1,36; 1,35; 1,34; 1,37; 1,38.
Требуется: а) составить статистический ряд;
б) найти статистическую функцию распределения ( );
в) изобразить полигон относительных частот.
7.3. В результате испытаний получены следующие статистические значения случайной величины X:
3,45; 3,47; 3,47; 3,43; 3, 46; 3,44; 3,40; 3,45; 3,41; 3,42; 3,47; 3,49; 3,41; 3,48; 3,43; 3,40; 3,43; 3,47; 3,45; 3,44; 3,41; 3,40; 3,48; 3,46; 3,51; 3,39; 3,50; 3,50; 3,47; 3,38; 3,44; 3,40; 3,40; 3,44; 3,47; 3,53; 3,46; 3,46; 3,52; 3,47; 3,41; 3,44; 3,47; 3,45; 3,44; 3,45; 3,47; 3,42; 3,44; 3,50; 3,45; 3,50; 3,42; 3,48; 3,40; 3,45; 3,48; 3,48; 3,46; 3,47; 3,44; 3,44; 3,47; 3,43; 3,44; 3,47; 3,44; 3,45; 3,44; 3,46; 3,46; 3,44; 3,44; 3,44; 3,44; 3,46; 3,44; 3,42; 3,50; 3,46; 3,48; 3,43; 3,40; 3,46; 3,46; 3,47; 3,45; 3,48; 3,42; 3,46; 3,48; 3,38; 3,45; 3,43; 3,52; 3,43; 3,50; 3,51; 3,41; 3,52.
Построить: а) интервальный статистический ряд;
б) статистический ряд, рассматривая в качестве значений середины интервалов;
в) статистическую функцию распределения ( );
г) гистограмму относительных частот.
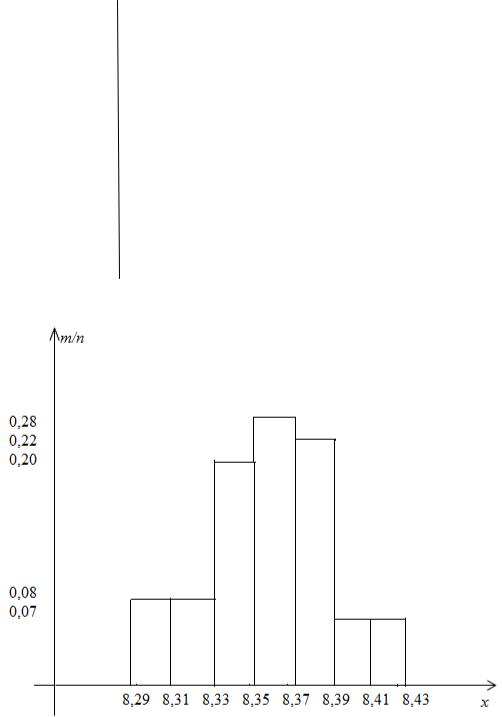
7.4. При измерении диаметров ста подшипниковых шариков, выбранных из большой партии шариков для определения стандартности, получены следующие результаты:
8,31; 8,42; 8,37; 8,40; 8,40; 8,30; 8,30; 8,42; 8,32; 8,29; 8,33; 8,36; 8,34; 8,37; 8,32; 8,36; 8,38,8,38; 8,33; 8,36; 8,40; 8,36; 8,32; 8,36; 8,36; 8,30; 8,30; 8,33; 8,35; 8,37; 8,37; 8,30; 8,41; 8,34; 8,33; 8,37; 8,34; 8,38; 8,29; 8, 34;

63
8,31; 8,36; 8,37; 8,30; 8,41; 8,34; 8,34; 8,37; 8,354 8,40; 8,34; 8,36; 8,37; 8,37; 8,41; 8,35; 8,38; 8,33; 8,36; 8,36; 8,36; 8,37; 8,36; 8,40; 8,37; 8,34; 8,37; 8,32; 8,35; 8,36; 8,37; 8,41; 8,36; 8,36; 8,36; 8,40; 8,34; 8,40; 8,34; 8,33; 8,35; 8,37; 8,34; 8,36; 8,37; 8,37; 8,35; 8,36; 8,34; 8,42; 8,36; 8,33; 8,34; 8,35; 8,36;8,32; 8,38; 8,32; 8,36; 8,37;
Построить: а) интервальный статистический ряд;
б) статистический ряд, рассматривая в качестве значений середины интервалов;
в) статистическую функцию распределения ( );
г) гистограмму относительных частот.
Ответы
7.1. а)
|
хi |
|
8,9 |
6,9 |
|
3,9 |
2,9 |
0,9 |
|
0,1 |
1,1 |
3,1 |
5,1 |
6,1 |
|||||||||||||||||||||||
|
i |
|
1 |
|
|
|
1 |
|
|
2 |
|
|
|
4 |
|
3 |
|
|
8 |
|
5 |
|
3 |
|
2 |
|
1 |
|
|||||||||
|
|
1 |
|
|
|
1 |
|
|
1 |
|
|
|
2 |
|
1 |
|
|
4 |
|
1 |
|
1 |
|
1 |
|
1 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30 |
|
|
30 |
|
15 |
15 |
10 |
|
15 |
6 |
|
10 |
15 |
30 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
≤ 8,9, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
0 |
|
|
при |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
1/30 |
|
при 8,9 < ≤ 6,9, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
1/15 |
|
при 6,9 < ≤ 3,9, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
2/15 |
|
при 3,9 < ≤ 2,9, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
4/15 |
|
при 2,9 < ≤ 0,9, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
б) |
|
( ) = |
|
11/30 при 0,9 < ≤ 0,1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
19/30 при 0,1 |
< ≤ 1,1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
4/5 при 1,1 |
< ≤ 3,1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
9/10 |
|
при 3,1 |
< ≤ 5,1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
29/30 при 5,1 |
< ≤ 6,1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
при |
|
|
|
> 6,1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
64
в)
7.2. |
а) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
хi |
|
1,31 |
1,33 |
|
1,34 |
1,35 |
|
1,36 |
|
1,37 |
1,38 |
1,39 |
1,40 |
1,41 |
||||||||||||||||||||||||
|
i |
|
1 |
|
1 |
|
|
|
|
4 |
|
5 |
|
6 |
|
|
5 |
|
3 |
|
2 |
|
2 |
|
1 |
|
|||||||||||||
|
|
1 |
|
1 |
|
|
|
|
2 |
|
1 |
|
1 |
|
|
1 |
|
1 |
|
1 |
|
1 |
|
1 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30 |
30 |
|
15 |
6 |
|
5 |
|
|
6 |
|
10 |
15 |
15 |
30 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
≤ 1,31, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
0 |
|
|
|
при |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
1/30 при 1,31 < ≤ 1,33, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
1/15 при 1,33 < ≤ 1,34, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
1/5 при 1,34 < ≤ 1,35, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
11/30 |
при 1,35 < ≤ 1,36, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
б) |
|
( ) = 17/30 |
при 1,36< ≤ 1,37, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
11/15 при 1,37 |
< ≤ 1,38, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
5/6 |
|
|
|
при 1,38 |
< ≤ 1,39, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
9/10 |
|
|
при 1,39 |
< ≤ 1,40, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
29/30 при 1,40 |
< ≤ 1,41, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
1 |
|
|
|
при |
|
|
> 1,41. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
7.3. |
а) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||

|
|
65 |
|
|
|
|
|
|
|
|
|
[хi; хi+1) |
i |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
[3,38; 3,40) |
3 |
|
0,03 |
||
[3,40; 3,42) |
12 |
|
0,12 |
||
[3,42; 3,44) |
12 |
|
0,12 |
||
[3,44; 3,46) |
27 |
|
0,27 |
||
[3,46; 3,48) |
25 |
|
0,25 |
||
[3,48; 3,50) |
9 |
|
0,09 |
||
[3,50; 3,52) |
8 |
|
0,08 |
||
[3,52; 3,54] |
4 |
|
0,04 |
||
Указания:
1) Из заданной выборки найти: xнаиб = 3,53, xнаим = 3,38,
xнаиб xнаим = 0,15.
2)Число интервалов определить по формуле:
k = 1+3,322 · lg n = 1 + 3,322· lg 100 = 1+6,644 = 7,644 ≈ 8.
3)Взять в качестве шага, то есть длины интервалов, число: 0,15 : 8 = 0,019 ≈ 0,02.
4)Из данной выборки найти i – число значений, попавших в промежуток
[хi; хi+1).
б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
3,39 |
3,41 |
3,43 |
3,45 |
3,47 |
3,49 |
3,51 |
3,53 |
|||||
|
|
|||||||||||||
|
|
i |
3 |
12 |
12 |
27 |
25 |
9 |
8 |
4 |
||||
|
|
|
0,03 |
0,12 |
0,12 |
0,27 |
0,25 |
0,09 |
0,08 |
0,04 |
||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
≤ 3,39, |
|
|
|
|
|
|
|
|
|
0 |
при |
|
|
|
|
|||||
|
|
|
|
0,03 |
при 3,39 < ≤ 3,41, |
|
|
|
|
|||||
|
|
|
|
0,15 |
при 3,41 < ≤ 3,43, |
|
|
|
|
|||||
|
|
|
|
0,27 |
при 3,43 < ≤ 3,45, |
|
|
|
|
|||||
|
|
|
|
0,54 |
при 3,45 < ≤ 3,47, |
|
|
|
|
|||||
в) |
( ) = |
0,79 |
при 3,47< ≤ 3,49, |
|
|
|
|
|||||||
|
|
|
|
0,88 |
при 3,49 < ≤ 3,51, |
|
|
|
|
|||||
|
|
|
|
0,96 |
при 3,51 < ≤ 3,53, |
|
|
|
|
|||||
|
|
|
|
1 |
при |
> 3,53. |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

66
г)
7.4. а)
[хi; хi+1) |
i |
|
|
|
|
|
|
||
|
|
|
|
|
[8,29; 8,31) |
8 |
0,08 |
||
[8,31; 8,33) |
8 |
0,08 |
||
[8,33; 8,35) |
20 |
0,20 |
||
[8,35; 8,37) |
28 |
0,28 |
||
[8,37; 8,39) |
22 |
0,22 |
||
[8,39; 8,41) |
7 |
0,07 |
||
[8,41; 8,43] |
7 |
0,07 |
||
б) |
|
|
|
|
|
|
|
|
|
|
|
i |
8,30 |
8,32 |
8,34 |
8,36 |
8,38 |
8,40 |
8,42 |
||
|
|
|||||||||
|
|
i |
8 |
8 |
20 |
28 |
22 |
7 |
7 |
|
|
|
|
0,08 |
0,08 |
0,20 |
0,28 |
0,22 |
0,07 |
0,07 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
67 |
|
|
|
|
|
|
|
≤ 8,30, |
|
|
0 |
при |
||||
|
|
0,08 |
при 8,30 < ≤ 8,32, |
||||
|
|
0,16 |
при 8,32 < ≤ 8,34, |
||||
в) |
( ) = |
0,36 |
при 8,34 < ≤ 8,36, |
||||
|
|
0,64 |
при 8,36 < ≤ 8,38, |
||||
|
|
0,86 |
при 8,38< ≤ 8,40, |
||||
|
|
0,93 |
при 8,40 < ≤ 8,42, |
||||
|
|
1 |
при |
> 8,42. |
|||
г) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
§8. Статистические оценки параметров
Точечные статистические оценки параметров распределения
Пусть собранный и обработанный статистический материал представлен в виде статистического ряда.
Определение 1. Точечной статистической оценкой параметра а распределения случайной величины называется приближенное значение а* этого параметра, вычисленного по статистическим данным.
68
Замечание 1. Любая точечная статистическая оценка некоторого параметра, вычисляемая на основе статистического ряда, должна удовлетворять трѐм требованиям:
при увеличении числа испытаний она должна сходиться по вероятности к оцениваемому параметру (свойство состоятельности);
математическое ожидание статистической оценки (как случайной величины при изменении числа испытаний) равно оцениваемому параметру
(свойство несмещенности);
при заданном объѐме выборки статистическая оценка имеет наименьшую дисперсию (свойство эффективности).
Определение 2. Статистической оценкой математического ожидания
называется среднее арифметическое статистических значений изучаемой случайной величины:
k
=1 ximi ,
i 1
где m1+m2+…+mk = n.
Замечание 2. Эта оценка математического ожидания обладает всеми свойствами оценок: состоятельности, несмещенности, эффективности.
Определение 3. Смещенной оценкой дисперсии D(x) называется выборочная дисперсия:
1 k m (x x)2
Dв= i i
i 1
Замечание 3. Эта оценка является смещенной, так как
M(Dв )= −1D(x).
Определение 4. Несмещенной оценкой дисперсии D(x) называется исправленная выборочная дисперсия:
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|||
s2= |
1 |
Dв= |
1 |
· |
mi (xi x)2 |
|||
−1 |
−1 |
|||||||
|
|
|
i 1 |
|||||
Замечание 4. При расчѐте s2 можно воспользоваться более удобной формулой:
|
|
|
k |
|
|
2 |
|
|
2 |
|
2 |
|
1 |
|
x |
n x |
|||||
|
m |
|
|
|
||||||
s |
= |
−1 i 1 |
i |
i |
|
|
|
|
|
|

69
Замечание 5. Выборочная дисперсия Dв и исправленная выборочная дисперсия s2 обладают свойством состоятельности. Оценка s2 не обладает свойством эффективности, но обладает свойством несмещенности, поэтому ее чаще чем Dв используют в качестве приближенного значения дисперсии D(x).
Определение 5. Оценкой среднего квадратического отклонения ζ(х)
называется квадратный корень из Dв или s2:
ζв= в или s = 2
Определение 6. Оценкой вероятности события А в n независимых испытаниях является относительная частота события А:
P*= ,
где m – число появления события А в n испытаниях.
Замечание 6. Эта оценка вероятности события А в n независимых испытаниях обладает свойствами несмещенности, состоятельности и эффективности.
Замечание 7. Если выборка состоит из вариант xi громоздкого вида, то для упрощения расчета выборочных точечных оценок параметров следует перейти к условным вариантам:
ui = − ,
где h – шаг между равноотстоящими вариантами; c – так называемый «ложный» нуль. Для них произвести расчет точечных оценок параметров:
|
|
k |
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= |
1 |
uiтi , |
Dв (u) = |
1 |
|
тi (ui u)2 |
, |
su2= |
|
· Dв (u). |
||
|
|
−1 |
||||||||||
|
i 1 |
|
i 1 |
|
|
|
||||||
Затем вычислить искомые точечные оценки: |
|
|
|
|
||||||||
= · h + c , |
|
Dв (x) = h2 · Dв (u), |
|
sx2 = h2 · su2 . |
|
|||||||
В качестве числа c обычно выбирают варианту xi0 , которая расположена в середине статистического ряда или имеет наибольшую частоту.
Интервальные оценки параметров нормального распределения
Для выборок небольшого объема вопрос точности оценок решается с помощью интервальных оценок.
При этом по вычисленной точечной оценке a* параметра a при заданной вероятности γ, называемой доверительной вероятностью, а также по некоторому числу ε , зависящему от γ и a* , строят интервал для истинного параметра a :
70 |
|
|
|
a* < a < a* + , |
|
|
|
чтобы выполнялось равенство: |
|
|
|
P (a* < a < a* + ) = γ . |
|
|
|
Число называется точностью оценки a*, границы интервала a* |
и |
a* + |
|
называются доверительными границами, интервал (a* |
и a* |
+ |
) – |
доверительным интервалом, вероятность γ доверительной вероятностью или надежностью интервальной оценки.
Определение 7. Интервальной оценкой математического ожидания m
нормального распределения при известной дисперсии σ2 называется интервал
( ; + ) , ε = zγ · ,
удовлетворяющий равенству:
Р ( < m < + ) = ,
где γ – заданная доверительная вероятность; m – истинное математическое ожидание; – точечная оценка математического ожидания; n – объем выборки; число zγ находится из уравнения Ф (zγ) = γ2 с помощью табл. П 2.2 функции Лапласа Ф (x), см. приложение 2.
Следовательно, интервальная оценка математического ожидания находится по формуле:
zγ· < m < + zγ· .
Определение 8. Интервальной оценкой математического ожидания m
нормального распределения при неизвестной дисперсии называется интервал
( ; + ) , ε = tγ · ,
удовлетворяющий равенству:
Р ( < m < + ) = ,
где γ – заданная доверительная вероятность; m – истинное математическое ожидание; – точечная оценка математического ожидания; s2 – точечная оценка дисперсии; n – объем выборки; число tγ вычисляется из уравнения
0 ; = 2 ,
с помощью табл. П 2.3 распределения Стьюдента (см. приложение 2).
