Правило вычисления обратной матрицы

1. Если матрица имеет обратную, то она невырожденная матрица

 

2. Cоставляем матрицу из алгебраических дополнений элементов матрицы А:

, тогда имеем .

3. Транспонируем полученную матрицу, т.е. меняем местами строки и столбцы, получаем матрицу, присоединенную к матрице А, обозначается А^*:

.

4. Обратная по отношению к матрице А имеет вид

ПРИМЕР 6. Найти матрицу А^-1, обратную для матрицы А, если .

Решение: , имеет обратную матрицу. Найдем алгебраические

дополнения

и составим из них матрицу

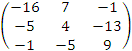. Полученную транспонируем .

Докажем, что АА^-1= Е = .

.

Решение систем линейных уравнений

Рассмотрим систему линейных алгебраических уравнений (СЛАУ) относительно n неизвестных x₁ , x₂ , ..., x_n:

Эта система в "свернутом" виде может быть записана так:

В соответствии с правилом умножения матриц рассмотренная система линейных уравнений может быть записана в матричной форме Ax=b, где

, , .

Матрица A, столбцами которой являются коэффициенты при соответствующих неизвестных, а строками - коэффициенты при неизвестных в соответствующем уравнении называется матрицей системы. Матрица-столбец b, элементами которой являются правые части уравнений системы, называется матрицей правой части или просто правой частью системы. Матрица-столбец x, элементы которой - искомые неизвестные, называется решением системы.

Система линейных алгебраических уравнений, записанная в виде Ax=b, является матричным уравнением.

Если матрица системы невырождена, то у нее существует обратная матрица и тогда решение системы Ax=b дается формулой: x=A ^-1 b.

 

Справедливо следующее утверждение (формулы Крамера).

Если определитель D=det A матрицы системы Ax=b отличен от нуля, то система имеет единственное решение x₁ , x₂ , ..., x_n, определяемое формулами Крамера

x_i =D_i / D, i=1,2, ..., n,

где D_i - определитель матрицы n -го порядка, полученной из матрицы A системы заменой i -го столбца столбцом правых частей b.

 

ПРИМЕР 2. Вычисление решения системы линейных уравнений по формулам Крамера.

 

Ответ: ( )

Метод Гаусса применим для решения системы линейных алгебраических уравнений c невырожденной матрицей системы. Идея метода Гаусса состоит в том, что систему n линейных алгебраических уравнений относительно n неизвестных x₁ , x₂ , ..., x_n

приводят последовательным исключением неизвестных к эквивалентной системе с треугольной матрицей

решение которой находят по рекуррентным формулам:

x_n =d_n , x_i = d_i -S ⁿ_k=i+1 c_ik x_k , i=n-1, n-2, ...,1.

ПРИМЕР 3. Вычисление решения системы линейных уравнений методом Гаусса.

 

Ответ: ( ).

Кривые второго порядка

Окружностью ( рис.1 ) называется геометрическое место точек, равноудалённых от данной точки О, называемой центром окружности, на расстояние R . Число R > 0 называется радиусом окружности.

Уравнение окружности имеет вид  

Например:

Переход от последнего уравнения к общему виду. Для удобства заменим

- общее уравнение окружности

Если центр окружности совпадает с началом координат, то уравнение окружности упрощается: . Например: .

  Пусть  Р ( х₁ , у ₁ ) – точка окружности ( рис.1 ), тогда  уравнение касательной к окружности в данной точке имеет вид:

  ( х₁ – х₀ ) ( х – х₀ )  + ( у₁ – у ₀ ) ( у – у ₀ ) = R ² .

 Условие касания прямой  y = m x + k  и окружности  х ²  +  у  ² = R ² :

  k ²  / ( 1 + m ² ) = R ² .

ПРИМЕР 1. Доказать, что уравнение х² + у² + 8х - 4у -5 = 0 является уравнением окружности. Найти ее центр и радиус.

Решение: Разделив уравнение на 2 и сгруппировав члены уравнения, получим х² - 4х +у² + у = 2. Дополним полученные выражения относительно переменных до полного квадрата двучлена

(х² - х + 4) - 4 +(у² + у + ) - = 2

.

Ответ: .

Эллипсом ( рис. ) называется множество точек плоскости, сумма расстояний которых до двух данных точек  F₁ и  F₂ , называемых  фокусами эллипса, есть величина постоянная, равная 2a.

- каноническое уравнение эллипса.

Здесь начало координат является центром симметрии эллипса, а оси координат – его осями симметрии. При  a > b фокусы эллипса лежат на оси ОХ , при  a < b фокусы эллипса лежат на оси ОY , а при  a = b  эллипс становится окружностью ( фокусы эллипса в этом случае совпадают с центром окружности). Таким образом,  окружность есть частный случай эллипса.

• Отрезок  F₁F₂ = 2 с,  где , называется фокусным расстоянием.

• Отрезок  AB = 2 a называется большой осью эллипса, а отрезок  CD = 2 b – малой осью эллипса.

• Число  e = c / a ,  e < 1 называется эксцентриситетом эллипса – мера сжатости эллипса. Форма эллипса зависит от его эксцентриситета (при e = 1 и b = 0 эллипс переходит в радиус F₁F₂ т.е. в уравнение окружности). Из этого следует, что окружность это частный случай эллипса, у которого фокусы слились в одну точку и совпали с его центром.

При изменении e от 0 до 1, эллипс будет из окружности, постепенно, сжимаясь,

трансформироваться во всё более и более вытянутую кривую пока не перейдет в

отрезок прямой F₁F₂.

- данное уравнение служит для определения формы эллипса.

Аналогично т.к. эллипс симметричен.

Достаточно рассмотреть его часть в 1 четверти и тогда y > 0 и х > 0, можно построить график функций

• Отрезок прямой соединяющий две точки эллипса называется хордой.

Оси симметрии – просто Ось эллипса.

Точка пересечения – центр.

• Точки в которых эллипс пересекает оси называются вершинами.

• Осями называют также отрезки B₁B = 2b, A₁A = 2a

Фокальная ось – ось на которой расположены фокусы.

Если , то величина - величина действительная и фокальной

осью будет 2a.

Если , то величина с – мнимая

величина. Фокусы будут на оси ординат, фокальной осью будет 2b.

Пусть  Р ( х₁ ,  у ₁ ) – точка эллипса, тогда  уравнение касательной к эллипсу в данной

точке имеет вид: =1.

Условие касания прямой  y = m x + k  и эллипса  х ² / a ²  +  у  ² / b ²  = 1 :

  k ²  = m ² a ² + b ²

ПРИМЕР 3. Найти каноническое уравнение эллипса, зная его большую полуось а =5 и эксцентриситет е = 0,6..

Решение: Зная, что e , найдем с = 0,6 . Но тогда квадрат малой полуоси эллипса каноническое равнение эллипса имеет вид .

Ответ: .

Гиперболой называется множество точек плоскости, абсолютная величина разности расстояний которых до двух данных точек  F₁ и  F₂ , называемых  фокусами гиперболы, есть величина постоянная, равная 2a.

Каноническое уравнение гиперболы.

.

Гипербола называется сопряженной с гиперболой

Числа a и b называются соответственно вещественной и мнимыми полуосями гиперболы.

• Ось гиперболы – прямая соединяющая её фокусы.

• Расстояние от начала координат до одного из фокусов гиперболы, называют фокусами расстояний гиперболы.

• Расстояние от начала координат до одной из вершин гиперболы называют большой или вещественной полуосью гиперболы a,

• Расстояние от вершины гиперболы до асимптоты в доле направления параллельное оси ординат называется малой или мнимой полуосью гиперболы b, .

• y = x – прямые являются асимптотами гиперболы.

• Отношение фокусного расстояния к большой полуоси гиперболы называется эксцентриситетом , . Эксцентриситет гиперболы всегда больше единицы.

• Расстояние от фокуса до гиперболы вдоль прямой параллельной Оси ординат называется фокальным параметром р, .

• Парацентрическое расстояние (r.p.) – расстояние от фокуса до ближайшей вершины гиперболы (в задачах связанных с движением)

• Предельным параметром называют расстояние от фокуса до одной из асимптот гиперболы. Предельный параметр равен малой полуоси гиперболы.

Пусть  Р ( х₁ ,  у ₁ ) – точка гиперболы, тогда  уравнение касательной к гиперболе в данной

точке имеет вид: =1.

Условие касания прямой  y = m x + k  и гиперболы  х ² / a ²  -  у  ² / b ²  = 1 :

  k ²  = m ² a ² + b ²

ПРИМЕР 1. Написать каноническое уравнение гиперболы, проходящей через точку М( , если фокальное расстояние гиперболы равно 20.

Решение: По условию 2с = 20, с =10. Запишем каноническое уравнение гиперболы По условию точка М принадлежит гиперболе, т.е. и второе уравнение для нахождения a и b: = 100 - .

Решим систему уравнений Решая систему относительно a и b(a>0, b>0), найдем . Искомым уравнением будет .

Ответ:

ПРИМЕР 2. Составить каноническое уравнение гиперболы, зная, что расстояние между ее фокусами равно 26, а эксцентриситет равен 13/12.

Решение: По условию 2с=26, с=13 и e =c/a=13/12. Следовательно, большая полуось гиперболы a = По формуле = 169 -144=25, . Уравнение гиперболы имеет вид .

Ответ: .

Параболой ( рис. ) называется множество точек плоскости, равноудалённых  от заданной точки  F , называемой фокусом параболы, и данной прямой, не проходящей через эту точку и называемой директрисой параболы.

Каноническое уравнение параболы ( рис. ) :

 y ² = 2 p x , р>0.

 Число р - параметр параболы. Начало координат О(0;0) – вершина параболы, а ось ОХ  является осью симметрии параболы. Точка F(p/2; 0) – фокус параболы, х = -р/2 директриса параболы.

 

Пусть  Р ( х₁ ,  у ₁ ) – точка параболы, тогда  уравнение касательной к параболе  в данной точке имеет вид: у ₁ y  = p ( x +  х₁ ) .          

 Условие касания прямой  y = m x + k  и параболы  y ² = 2 p x: 2 m k   = p .

ПРИМЕР 4. Составить уравнение параболы, симметричной относительно оси Ох, с вершиной в начале координат, если длина некоторой хорды этой параболы, перпендикулярной оси Ох. равна 16, а расстояние этой хорды от вершины равно 6.

Решение: Так как известны длина хорды и расстояние ее от вершины, то, следовательно, известны координаты конца этой хорды – точки М, лежащей на параболе. Уравнение параболы имеет вид y ² = 2px; полагая в нем х = 6 и у = 8, находим 8²=2р

2 = . Итак, уравнение параболы имеет вид y ² = x, F(8/3;0)

Ответ: y ² = x.

Теория пределов

Число А называется пределом функции f(x) при , если для любого числа можно указать такое , что для любого , удовлетворяющего неравенству выполняется неравенство . Функция f(x) называется бесконечно малой при , если . Функция f(x) называется бесконечно большой при , если или .

Свойства б/м и б/б функций:

• Если f(x) и g(x) – б/м при , то их сумма f(x) + g(x) при также является б/м.

• Если f(x) - б/м при , а F(x) – ограниченная функция, то f(x)* F(x) есть функция б/м.

• Если при функция f(x) имеет конечный предел , а функция - б/б, то .

• Если f(x) - б/м при , то 1/ f(x) – б/б, причем в окрестности точки a функция f(x) в нуль не обращается.

• Если f(x) - б/б при , то 1/ f(x) – б/м.

Теоремы о пределах.

1. Если f(x) имеет предел при , то этот предел единственный.

2. Предел суммы функций равен сумме пределов этих функций.

3. Предел произведения функций равен произведению пределов этих функций.

4. Предел частного двух функций равен частному пределов этих функций.

Следствия

5. Постоянный множитель можно выносить за знак предела

6. Если n – натуральное число, то .

Замечательные пределы:

1) и ; и .

2) и .

ПРИМЕР 1. На основании определения предела переменной величины доказать, что

.

Решение: На основании определения предела переменной величины

. При

ПРИМЕР 2. Найти пределы функции:

а) Решение: При получаем неопределенность Сократим дробь

и вычислим =

б) . Решение: При получаем неопределенность Сократим дробь, умножив числитель и знаменатель дроби на одно и тоже выражение, сопряженное числителю. .

=

в) . Решение: При получаем неопределенность Сократим дробь, разложив числитель и знаменатель дроби на множители, найдя корни квадратного трехчлена.

=

г) . При получаем неопределенность

Решение: Сведем к бесконечно малым величинам, разделив каждое слагаемое числителя и знаменателя на наибольшую степень, т.е. х².

= ,

так как при и т.д.

д) . Решение: Разобьем дробь на две дроби, применяя теоремы о пределах, и воспользуемся формулой первого замечательного предела

=

е) Решение: Разобьем дробь на две дроби и воспользуемся формулой второго замечательного предела.

= = = .

ж) . Решение: Разобьем дробь на две дроби и воспользуемся одной из формул второго замечательного предела. = = .

Производная функции.

Производной функции y=f(x) называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремиться к нулю

_{Правила:}

1.

2.

3.

4. Если y=f(u) и u=q(x) дифференцируемые функции своих аргументов, то производная сложной функции y=f(q(x)) существует и равна произведению производной данной функции y по промежуточному аргументу u на производную промежуточного аргумента u по независимой переменой x.

.

Следствие: Постоянный множитель выносится за знак производной

Формулы дифференцирования для сложной функции, где u(x) –внутренняя функция

Производной второго порядка или второй производной функции y=f(x) называется производная от ее первой производной функции . Она обозначается

. Аналогично определяются и обозначаются производные третьего, четвертого и других порядков

.