3.3. Методы измерений: непосредственной оценки и сравнения.

Метод непосредственной оценки — метод измерений, при котором значение величины определяют непосредственно по показывающему средству измерений.

- метод сравнения с мерой – измеряемую величину сравнивают величину с воспроизводимой мерой;

- нулевой – метод, при котором измеряемую величину и величину, воспроизводимой мерой доводят до ноля;

- замещение – измеряемую величину замещают известной величиной воспроизводимой меры;

- дополнения – значение измеряемой величины с расчетом, чтобы на прибор воздействовала сумма ранее заданного значения;

- дифференцированный – измеряемая величина сравнивается с однородной величиной, имеющих начальное значение известное, но незначительно отличающиеся от измеряемой величины, при этом измеряется разность между значениями.

Раздел 4 Подготовка эксперимента

Уточнение цели и данных об условиях проведения эксперимента и физической величине. Физические величины: род, вид, характер изменения по времени и по значению. Формулирование (выбор) модели объекта измерения. Требования, предъявляемые к модели. Приближенные и точные модели объекта (в виде дифференциального уравнения, скалярной величины, векторной величины, периодического сигнала) и их связь с постановкой измерительной задачи.

Раздел 4

4.1. Физические величины: род, вид, характер изменения по времени и по значению. Формулирование (выбор) модели объекта измерения.

Физическая величина — свойство, общее в качественном отношении для многих физических объектов, процессов, явлений, но индивидуальное в количественном отношении. В системе Си существует

Значение физической величины — одно или несколько (в случае тензорной физической величины) чисел, характеризующих эту физическую величину, с указанием единицы измерения, на основе которой они были получены.

Размерность физической величины — единица измерения, фигурирующая в значении физической величины. Как правило, у физической величины много различных размерностей: например, у длины — метр, см

Единство измерений обеспечивается международной системой единиц СИ, в которой содержится 6 основных единиц (ниоткуда не выводимых: килограмм, метр, секунда, ампер, кельвин, моль и кандела) и порядка двадцати дополнительных (выводимых из основных шести).

Истинное значение — такое значение физической величины, которое идеальным образом отражает качественным и количественным отношением соответствующие свойства объекта.

Действительное значение — значение физической величины, наиболее близко расположенное к истинному значению и полученное с точностью, удовлетворяющей использованию данного результата¹.

1. По возможности производить работу

   1. активные  u, i, e 

   2. пассивные  R, C, L 

2. По характеру изменений

   1. детерминированные (значение можно предсказать)

   2. случайные (изменяются по случайному закону)

3. По возможным значениям

   1. аналоговые — интервал [x_min, x_max] содержит бесконечно большое число значений величины:

2. квантованные — интервал [x_min, x_max] содержит конечное либо счетное число значений величины:

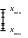
4. По значениям в определенные моменты времени:

   1. непрерывные:

2. дискретные:

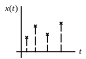
4.2. Уточнение цели и данных об условиях проведения эксперимента и физической величине. Требования, предъявляемые к модели. Приближенные и точные модели объекта (в виде дифференциального уравнения, скалярной величины, векторной величины, периодического сигнала) и их связь с постановкой измерительной задачи

Моделью объекта называется отражение свойств реального объекта.

Адекватность модели — степень приближения этой модели к реальному объекту

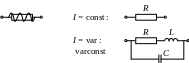
При построении математической модели объекта измерения неизбежно приходится идеализировать те или иные его свойства. Модель никогда не может полностью описывать все свойства объекта измерений. Она отражает с определенной степенью приближения некоторые из них, имеющие существенное значение для решения данной измерительной задачи. Модель строится до измерения на основе априорной информации об объекте и с учетом цели измерения. Измеряемая величина определяется как параметр принятой модели, а его значение, которое можно было бы получить в результате абсолютно точного измерения, принимается в качестве истинного значения данной измеряемой величины. Эта неизбежная идеализация, принятая при построении модели объекта измерения, обуславливает неизбежное несоответствие между параметром модели и реальным свойством объекта, которое называется пороговым. Пороговое несоответствие принципиально ограничивает достижимую точность измерений при принятом определении измеряемой ФВ. Изменения и уточнения цели измерения, в том числе и такие, которые требуют повышения точности измерений, приводят к необходимости изменять или уточнять модель объекта измерений и переопределять понятие измеряемой величины. Основной причиной переопределения является то, что пороговое несоответствие ранее принятого определения не позволяет повысить точность измерения до уровня требуемой. Вновь введенный измеряемый параметр модели также может быть измерен лишь с погрешностью, которая в лучшем случае равна погрешности, обусловленной пороговым несоответствием. Поскольку принципиально невозможно построить абсолютно адекватную модель объекта измерения, то нельзя устранить пороговое несоответствие между измеряемой ФВ и описывающим ее параметром модели объекта измерений. Отсюда вытекает важное следствие ₁: истинное значение измеряемой величины отыскать невозможно. Модель можно построить только при наличии априорной информации об объекте измерения. При этом чем больше информации, тем более адекватной будет модель и соответственно точнее и правильнее будет выбран ее параметр, описывающий измеряемую ФВ. Следовательно, увеличение априорной информации уменьшает пороговое несоответствие. Из этого следствия вытекает, что при отсутствии априорной информации измерение принципиально невозможно. В то же время максимально возможная априорная информация заключается в известной оценке измеряемой величины, точность которой равна требуемой. В этом случае необходимости в измерении нет.

Требования, предъявляемые к модели: 1) представлять объект в упрощенном виде, но с допустимой степенью простоты для данного вида и цели исследования, проблемы и задач; 2) давать возможность перехода от модельной информации к реальной.

Вопрос Сущность планирования измерительного эксперимента

Планирование эксперимента (англ. experimental design techniques) — комплекс мероприятий, направленных на эффективную постановку опытов. Основная цель планирования эксперимента — достижение максимальной точности измерений при минимальном количестве проведенных опытов и сохранении статистической достоверности результатов.

Планирование эксперимента применяется при поиске оптимальных условий, построении интерполяционных формул, выборе значимых факторов, оценке и уточнении констант теоретических моделей и др.

Вопрос Однофакторный и многофакторный эксперимент

 

Однофакторный пассивный эксперимент проводится путем выполнения пар измерений в дискретные моменты времени единственного входного параметра и соответствующих значений выходного параметра (рис.1,а). Аналитическая зависимость между этими параметрами вследствие случайного характера возмущающих воздействий рассматривается в виде зависимости математического ожидания от значения , носящей название регрессионной. Целью однофакторного пассивного эксперимента является построение регрессионной модели - установление зависимости .

Многофакторный пассивный эксперимент проводится при контроле значений нескольких входных параметров (1.,б) и его целью является установление зависимости выходного параметра от двух или более переменных .

Полный факторный эксперимент предполагает возможность управлять объектом по одному или нескольким независимым каналам (см. рис.1.5,в).

В общем случае, схема эксперимента может быть представлена в виде, представленном на рис.1., в. В схеме используются следующие группы параметров:

управляющие (входные )

параметры состояния (выходные )

возмущающие воздействия ( )

При многофакторном и полном факторном эксперименте выходных параметров может быть несколько. Пример такого пассивного многофакторного эксперимента будет рассмотрен в шестой главе настоящей книги.

Управляющие параметры представляют собой независимые переменные, которые можно изменять для управления выходными параметрами. Управляющие параметры называют факторами. Если (один управляющий параметр), то эксперимент однофакторный. Многофакторный эксперимент соответствует конечному числу управляющих параметров. Полный факторный эксперимент соответствует наличию возмущающих воздействий в многофакторном эксперименте.

Диапазон изменения факторов или число значений, которое они могут принимать называется уровнем фактора.