Задание 2.
Даны точки плоскости А, В, С. Требуется:
составить уравнение окружности, проходящей через эти точки, определить координаты центра N и величину R радиуса окружности;
написать уравнение гиперболы, проходящей через точки В и С, найти полуоси, фокусы, эксцентриситет и асимптоты;
построить точки и кривые в системе координат.
|
А ( 2; 4) |
В (-5;-3) |
С ( 3; 1) |
Задание 3.
Решить системы линейных уравнений с помощью определителей.
Задание 4.
Решить системы линейных уравнений методом Гаусса.
Задание 5.
Исследовать систему линейных уравнений на совместность и решить ее, если она совместна
Задание 6.
Представить систему линейных уравнений в матричной форме и решить систему с помощью обратной матрицы; пользуясь правилом умножения матриц, показать, что произведение матрицы системы на обратную ей матрицу равно единичной матрице Е.
Задание 7.
Доказать образуют ли вектора (а, в, с) базис. Найти координаты вектора х в этом базисе.
а(9;7;-1); в(0;-2;-4); с(1;9;-3) , х(1;5;-6).
Задание 8.
Даны координаты вершин пирамиды ABCD.
Требуется:
записать векторы в системе орт и найти модули этих векторов;
найти угол между векторами
найти проекцию вектора на вектор ;
|
A(-4;5;-5) |
B(-3;3;-3) |
C(7;7;5) |
D(4;9;3) |
Задание 9.
Даны координаты точек А, В, С.Требуется:
Составить канонические уравнения прямой АВ.
Составить уравнение плоскости Q, проходящей через точку С перпендикулярно прямой АВ.
Найти точку пересечения прямой АВ с плоскостью Q.
Вычислить расстояние от точки С до прямой АВ.
Найти точку D, симметричную точке С относительно прямой АВ.
|
A(-1;2;-2) |
B(3;4;-6) |
C(0;1;-6) |
Задание 10.
Прямая линия задана в виде пересечения двух плоскостей. Написать канонические уравнения этой прямой.
Задание 11.
Найти пределы функций:
,
;
;
;
б)
;
в)
;
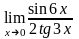г)
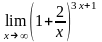
Задание 12.
Найти производную , пользуясь формулами дифференцирования.
б)
в)
Задание 13.
В задачах дана функция Z=F(x, у). Найти полный дифференциал dz;
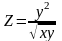
Задание 14.
Найти указанные неопределенные интегралы и вычислить определенные интегралы
а)
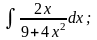б)
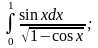в)
Задание 15.
Найти ООФ и изобразить эту область на плоскости ХОУ:
Задание 16.
Найти наибольшее и наименьшее значение
функции
А) в прямоугольнике [-6;6]х[-4;4];
В)
.
Задание 17.
Найти
экстремумы функции:
.
Задание 18.
Найти
интервал сходимости степенного ряда и
исследовать сходимость на концах
интервала сходимости:
.
Задание 19.
Найти
координаты центра тяжести фигуры,
ограниченной кривыми
.
Задание 20.
Переходя
к сферическим координатам вычислить
,
где область V ограничена
поверхностью
.
Задание 21.
Вычислить
криволинейный интеграл
,
где L дуга параболы
от точки А(0;0) до точки В(1;2).
Задание 22.
Найти
общее решение дифференциального
уравнения
Задание 23.
Найти частное решение дифференциального уравнения, удовлетворяющего заданным начальным условиям:
А)
;
В)
.
19 Вариант.
Задание 1.
Даны вершины треугольника АВС. Требуется найти:
длины сторон АВ и АС, их уравнения и угловые коэффициенты;
величину угла А в градусах;
уравнение биссектрисы АR угла А;
точку пересечения медиан треугольника АВС;
уравнение высоты CN и точку N её пересечения со стороной АВ;
уравнение прямой l, проходящей через вершину В параллельно стороне АС и её точку пересечения с высотой CN;
координаты точки D, симметричной точке С и лежащей на медиане СМ;
вычислить площадь четырехугольника АDBC.
|
А (-10;-3) |
В -2;-9) |
С ( 2; 6) |
|
|
|
|