Вопрос 3. Параллельное соединение r, l, с

    Если к зажимам электрической цепи, состоящей из параллельно соединенных элементов R, L, С (рисунок 2.18), приложено гармоническое напряжение u = Umcosωt, то гармонический ток, проходящий через эту цепь, равен алгебраической сумме гармонических токов в параллельных ветвях (первый закон Кирхгофа): i = iR + iL + iC.

    Ток iR в сопротивлении R совпадает по фазе с напряжением и, ток iL в индуктивности L отстает, а ток iC в емкости Сопережает напряжение на π/2 (рисунок 2.19).

    Следовательно, суммарный ток i в цепи равен

(2.20)

Уравнение (2.20) представляет собой тригонометрическую форму записи первого закона Кирхгофа для мгновенных значений токов. Входящая в него величина   называется реактивной проводимостью цепи, которая в зависимости от знака может иметь индуктивный (b > 0) или емкостный (b < 0) характер. В отличие от реактивной проводимости b активная проводимость g = l/R всегда положительна.

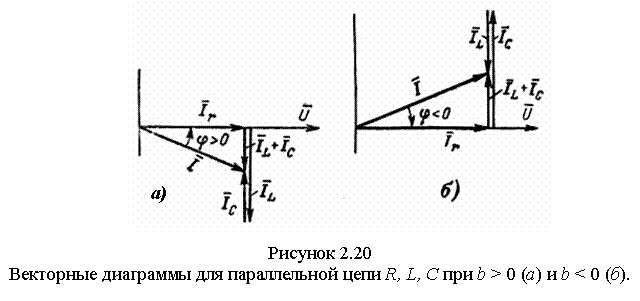
    Для нахождения Im и φ воспользуемся векторной диаграммой, соответствующей уравнению (2.20) (рисунок 2.20, а и б). Прямоугольный треугольник с катетами IR и [IL+IC] и гипотенузой I называется треугольником токов. Треугольник токов построен на рисунке 2.20, а для b >0, а на рисунке 2.20, б − для b < 0.

    Из треугольника токов следует, что 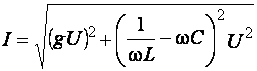  или I = yU; Im=yUm

Здесь 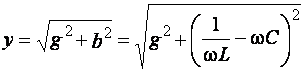 (2.21)

    полная проводимость рассматриваемой параллельной цепи.

    Активная, реактивная и полная проводимости относятся к числу основных понятий, применяемых в теории электрических цепей.

    Угол фазового сдвига тока i относительно напряжения и равен:

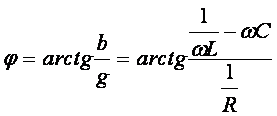. (2.22)

    Если задано напряжение и = Umcos(ωt + y) на зажимах цепи с параллельно соединенными R, L и С, то ток определяется по формуле

 i = yUmcos(ωt  + y - φ).

    Угол φ, как и в предыдущем случае, отсчитывается на временной диаграмме ωt от напряжения к току, а на векторной диаграмме - от тока к напряжению; он является острым или прямым углом

|φ|   .

    Угол φ положителен при индуктивном характере цепи, т.е. при b > 0; при этом ток отстает по .фазе от напряжения. Уголφ отрицателен при емкостном характере цепи, т.е. при b < 0; при этом ток опережает по фазе напряжение. Ток совпадает с напряжением по фазе при b = bR - bC = 0, т.е. при равенстве индуктивной и емкостной проводимостей. Такой режим работы электрической цепи называется резонансом токов.

    Из (2.21) и (2.22) следует, что активная и реактивная проводимости цепи связаны с полной проводимостью формулами:

 g = ycosφ; b = уsinφ. (2.23)

    Умножив правые и левые части выражений (2.23) на действующее значение напряжения U, получим действующие значения токов в ветвях с активной и реактивной проводимостями изображаемые катетами треугольника токов и называемые активной и реактивной составляющими тока:

Ia = gU = ycosφU = Icosφ;

 Ip = bU = ysinφU = Isinφ.

Как видно из треугольников токов и уравнений (2.24), активная и реактивная составляющие тока связаны с действующим значением суммарного тока формулой

 .

    Разделив стороны треугольника токов на U, получим прямоугольный треугольник проводимостей, подобный треугольнику напряжений (рисунок 2.21, а, б).

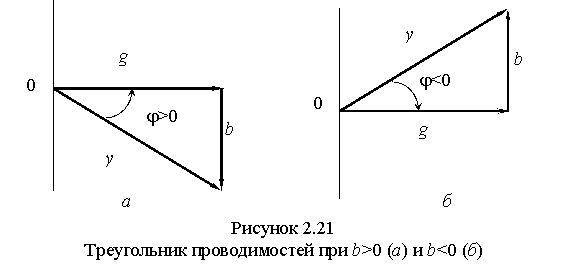
    Треугольник проводимостей служит геометрической интерпретацией уравнений (2.21) и (2.22); активная проводимостьg откладывается по горизонтальной оси вправо, а реактивная проводимость b в зависимости от ее знака откладывается вниз (b > 0) или вверх (b < 0).

    Угол φ в треугольнике проводимостей отсчитывается, от гипотенузы у к катету g, что соответствует отсчету  φ в треугольнике токов от I = yU к Ia = gU.

    Для характеристики конденсаторов, представляемых цепью с емкостной и активной проводимостями, применяется понятие добротность конденсатора QC = b/g = ωCR, которое равнозначно тангенсу угла |φ| конденсатора. Обратная величина называется тангенсом угла диэлектрических потерь конденсатора tgδ = l/QC (угол диэлектрических потерь δдополняет угол |φ| до 90°).

    Чем больше сопротивление R, тем больше (при прочих равных условиях) добротность конденсатора и тем меньше угол потерь.

    Добротность конденсаторов для разных частот и диэлектриков колеблется в широких пределах, примерно от 100 до 5000. Слюдяные конденсаторы обладают большей добротностью, чем керамические. Добротность конденсаторов, применяемых в высокочастотной технике, примерно в 10 раз превышает добротность индуктивных катушек.