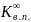- •Показатель преломления для основной длины волны е округляется до 5 значащих цифр!
- •1.Расчет плосковыпуклой линзы
- •2 Способ определения радиуса
- •Расчет линзы на минимум сферической аберрации 3-го порядка
- •Конструктивные параметры линзы
- •Формулу для главного отрезка необходимо знать наизусть!
- •Пояснения:
Пояснения:
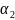 -
первое значение угла
-
первое значение угла
np h alpha y beta
0 * * * * 0.000000 * * * * 1.000000
1 69.999997 0.577715 -16.820000 0.505472
2 68.440167 1.000000 -18.184774 0.757088
3 -0.000000 * * * * -69.999997
C, P, W- суммируются значения 1 и 2
np C P W PI B Pw Bw
1 -0.00795 0.98181 -0.60452 0.57772 0.00000 -1.30334 0.00000
2 -0.00581 0.88476 0.74528 0.06657 0.00000 0.21586 0.00000
Где
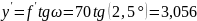
 -
коэффициент изопланатизма (в распечатке
он обозначается Eta)
-
коэффициент изопланатизма (в распечатке
он обозначается Eta)
Осевой пучок ____Л0____ ____Л1____ ____Л2____
== M = 100tg σ'== dS'=== dY'=== dS'=== dY'=== dS'=== dY'= dS'12 = Eta %=
7.800 11.34 -0.8132-0.0922-1.2850-0.1467-0.3348-0.0377-0.9503 1.0778
6.755 9.77 -0.6078-0.0594-1.0802-0.1063-0.1289-0.0125-0.9513 0.8068
5.515 7.95 -0.4038-0.0321-0.8767-0.0701 0.0757 0.0060-0.9524 0.5367
3.900 5.60 -0.2013-0.0113-0.6747-0.0380 0.2787 0.0155-0.9535 0.2679
0.000 0.00 -0.0000 0.0000-0.4740 0.0000 0.4806 0.0000-0.9546
Берется значение для края (в данном случае 1.0778) и делится на 100(так как он дан в процентах).
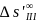 -
продольная сферическая аберрация
третьего порядка
-
продольная сферическая аберрация
третьего порядка
 -
поперечная сферическая аберрация
третьего порядка
-
поперечная сферическая аберрация
третьего порядка
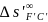 -
хроматизм увеличения (первый, встречающийся
в таблице)
-
хроматизм увеличения (первый, встречающийся
в таблице)
- хроматизм положения (второй, встречающийся в таблице)
Параметры, аберрации |
Плосковыпуклая линза |
Выпукло-плоская |
Линза с минимальной сферической аберрацией III-го порядка |
Парабалоидно-плоская линза |
Значения
аберрационных параметров
|
||||
|
|
|
0,577715 |
|
|
|
|
-0,0138 |
|
|
|
|
1,8666 |
|
|
|
|
0,1408 |
|
|
|
|
-0,9545 |
|
|
|
|
-0,8025 |
|
|
|
|
0,1789 |
3 |
|
|
|
0.0184 |
4 |
|
|
|
0,0917 |
5 |
|
|
|
-0,9503 |
6 |
|
|
|
-0,8132 |
7 |
|
|
|
0,1844 |
8 |
|
|
|
0,0200
|
9 |
Вычислить
аберрации высших порядков
|
||||
|
7-3 |
|
|
|
|
9-5 |
|
|
|
- коэффициент изопланатизма
C – хроматический параметр
P – аберрационный параметр Р ( характеризует сфер. аберрацию)
W – аберрационный параметр W (даблвэ!!!!, характеризует кому)
- хроматизм увеличения (в таблице их два; первое – хроматизм увеличения, второе – хроматизм положения)
- меридиональная кома 3-го порядка
- поперечная сферическая аберрация 3-го порядка
Вывод по работе:
В данной работе был выполнен аберрационный анализ и габаритный расчёт и линз. Среди линз со сферическими поверхностями наилучшей является линза, расчитаная на минимум сферической аберрации, затем следует выпукло-плоская. Наихудшей является плосковыпуклая линза.
Отличительной чертой параболоидно-плоской линзы является то, что её сферическая аберрация положительна. Наилучшая линза - параболоидно-плоская. Введение асферики позволяет существенно уменьшить величину сферической аберрации.
Ниже приведены значения сферической аберрации 3-го порядка (по убыванию):

Берется это с таблицы (4 значения):

Аберрации высших порядков и кома убывают в том же порядке.
Необходимо сделать графики:
На фото ниже - пример выполнения графиков. Всего должно получиться 12 кривых. Для каждой линзы 3 графика, линзы 4.
Графики берутся с распечаток: 1 график - по оси х - дельта эс штрих по оси у - 100 тангенс сигма штрих 2 график - по оси х - дельта игрик штрих по оси у - 100 тангенс сигма штрих 3 график - по оси х - дельта игрик штрих по оси у – M





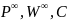 бесконечно тонких линз и аберраций
линз конечной толщины
бесконечно тонких линз и аберраций
линз конечной толщины
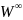
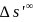
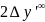
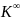
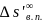 и
и