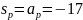- •Показатель преломления для основной длины волны е округляется до 5 значащих цифр!
- •1.Расчет плосковыпуклой линзы
- •2 Способ определения радиуса
- •Расчет линзы на минимум сферической аберрации 3-го порядка
- •Конструктивные параметры линзы
- •Формулу для главного отрезка необходимо знать наизусть!
- •Пояснения:
О чем вообще эта работа? Нам предлагается рассчитать, а так же провести аберрационный анализ для 4 линз: плосковыпуклая, выпукло-плоская, рассчитанная на минимум сферической аберрации и параболоидно-плоская линза.
Исходные данные:
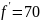 ;
- заднее фокусное расстояние
;
- заднее фокусное расстояние
D/f’ =1:4,5 - относительное отверстие ( где знаменатель этой дроби называется диафрагменным числом K)
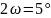 - угловое поле
- угловое поле
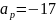 - положение входного зрачка
- положение входного зрачка
Марк стекла: ОК2 - стекло особый крон 2
 – показатель преломления для основной
длины волны e
(зеленый, λ = 546,07 нм).
– показатель преломления для основной
длины волны e
(зеленый, λ = 546,07 нм).
Показатель преломления для основной длины волны е округляется до 5 значащих цифр!
Значащие цифры это не после запятой! Это сколько ВСЕГО цифр!
Допустим, нам задан показатель преломления для основной длины волны стекла К8:
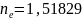 - здесь 6 цифр, округляем до 1,5183
- здесь 6 цифр, округляем до 1,5183
1.Расчет плосковыпуклой линзы

f’ – заднее фокусное расстояние( отрезок отсчитывается от задней главной точки Н’до задней точки фокуса F’);
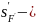 задний
фокальный отрезок( отрезок отсчитывается
от точки поверхности до задней точки
фокуса F’);
задний
фокальный отрезок( отрезок отсчитывается
от точки поверхности до задней точки
фокуса F’);
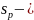 положение
входного зрачка( отрезок отсчитывается
от точки поверхности до точки входного
зрачка p);
положение
входного зрачка( отрезок отсчитывается
от точки поверхности до точки входного
зрачка p);
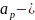 положение
входного зрачка ( отрезок отсчитывается
от передней главной точки Н до осевой
точки входного зрачка p);
положение
входного зрачка ( отрезок отсчитывается
от передней главной точки Н до осевой
точки входного зрачка p);
 передний главный отрезок (отрезок
отсчитывается от передней главной точки
Н до точки поверхности)
передний главный отрезок (отрезок
отсчитывается от передней главной точки
Н до точки поверхности)
Нам задано относительное отверстие:
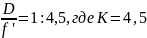
Также
известно заднее фокусное расстояние
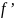 =70
мм
=70
мм
Определим диаметр входного зрачка:


Рисунок к определению светового диаметра
Пояснение к рисунку:
Световой диаметр определяется удвоенной высотой верхнего полевого луча( определяется максимальной высотой луча, а на рисунке максимальную высоту имеет верхний полевой луч)
y’ –величина изображения
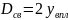
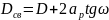

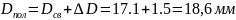 ,
где
,
где
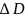 - припуск на закрепление при креплении
- припуск на закрепление при креплении
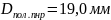 - полный диаметр по нормальному
ряду(есть такая таблица, где приведены
нормальные линейные размеры, в том числе
и диаметры; всегда берется близкое
большее по значению число; в нашем случае
ближайшее к 18,6 в этом ряде числе – 19)
- полный диаметр по нормальному
ряду(есть такая таблица, где приведены
нормальные линейные размеры, в том числе
и диаметры; всегда берется близкое
большее по значению число; в нашем случае
ближайшее к 18,6 в этом ряде числе – 19)
Определим конструктивные параметры линзы:
Что такое конструктивные параметры?
К
конструктивным параметрам относят:
радиусы кривизны
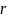 ,
толщины
,
толщины
 ,
показатели преломления n,
а так же отклонения от этих величин -
,
показатели преломления n,
а так же отклонения от этих величин -
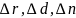
Первая поверхность плоская, значит, что её радиус кривизны равен 0:

Радиус второй поверхности найдем из формулы линзы:
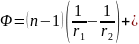
Формулу линзы нужно выучить наизусть!
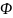 - оптическая сила линзы ( измеряется
в диоптриях, дптр)
- оптическая сила линзы ( измеряется
в диоптриях, дптр)
Поскольку
первая поверхность у нас плоская (её
радиус кривизны
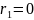 ),
то формула упрощается (второе слагаемое
обращается в ноль, во второй скобке
убирается 1/r1):
),
то формула упрощается (второе слагаемое
обращается в ноль, во второй скобке
убирается 1/r1):
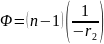
Так же известна другая формула для оптической силы:
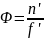
Поскольку наша линза находится в воздухе (n’ = 1), то формула принимает вид:

Приравняем:
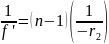
, откуда
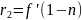

Радиус – 6 значащих цифр! Т.е. их всего в записи 6.
2 Способ определения радиуса
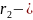 найдем из уравнения параксиального
луча при нормировке начальных координат:
найдем из уравнения параксиального
луча при нормировке начальных координат:
Что такое параксиальная оптика? Параксиальная оптика – оптика, где углы и высоты лучей очень малы (стремятся к бесконечно малой величине).
Нормировка начальных координат – нормировка начальных координат первого и второго параксиальных лучей.

Первый параксиальный луч идет на край входного зрачка под углом в 0 (параллельно оптической оси), выходит из системы под углом 1; Второй параксиальный луч идет через середину входного зрачка под углом 1.
Высоты и
углы первого параксиального луча
обозначаются
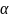 и
и
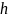
Высоты и
углы второго параксиального луча
обозначаются
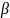 и y
и y
Нормировка
начальных координат 1 параксиального
луча:
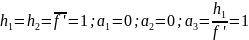 .
.

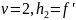
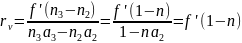
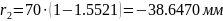
Вычислим
толщину линзы:

d – толщина. Округляется до десятых!
k- стрелка прогиба. Округляется до сотых!
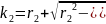
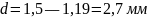
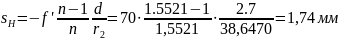

Конструктивные параметры плосковыпуклой линзы:
 марка стекла
марка стекла

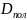
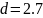 1.5521 72.64 ОК2
17.1 19.0
1.5521 72.64 ОК2
17.1 19.0
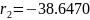
Выполним аберрационный анализ в области аберраций 3-го порядка:
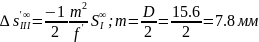
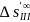 -
продольная сферическая аберрация 3-го
порядка.
-
продольная сферическая аберрация 3-го
порядка.
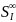 -
первая сумма Зейделя ( характеризует
сферическую аберрацию)
-
первая сумма Зейделя ( характеризует
сферическую аберрацию)
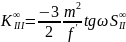
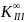 -
меридиональная кома 3-го порядка
-
меридиональная кома 3-го порядка
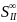 - вторая сумма Зейделя (характеризует
кому)
- вторая сумма Зейделя (характеризует
кому)

P-
аберрационный параметр
Если
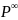 - основной аберрационный параметр (
основной он тогда, когда мы нормировали
начальные координаты, т.е. координаты
первого параксиального луча:
- основной аберрационный параметр (
основной он тогда, когда мы нормировали
начальные координаты, т.е. координаты
первого параксиального луча:
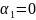 ,
,
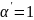 ,
,
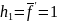 ,
второго параксиального луча:
,
второго параксиального луча:
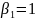 ,
,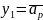 )
)
Если
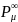 - основной аберрационный параметр P
для бесконечно тонкой линзы.
- основной аберрационный параметр P
для бесконечно тонкой линзы.
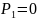 (первая поверхность – плоская)
(первая поверхность – плоская)
Формула для аберрационного параметра P (общий вид):
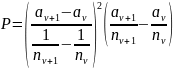

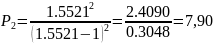
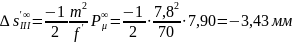
У положительных линз значения продольной сферической аберрации третьего порядка отрицательные, а у отрицательных линз положительные!
Исключение составляет параболоидно-плоская линза.
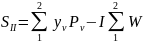
Нормировка
начальных координат 2 параксиального
луча:
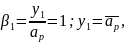 где
где
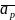 -
приведенное положение входного зрачка.
-
приведенное положение входного зрачка.
Приведенная величина – значит поделенная на заднее фокусное расстояние !
При такой
нормировке инвариант Лагранжа-Гельмгольца
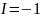 ,
поэтому:
,
поэтому:
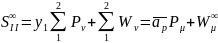
Формула для аберрационного параметра W (общий вид):
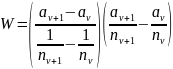
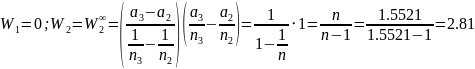

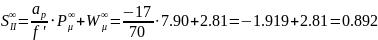
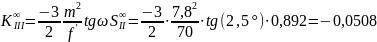
Расчет выпукло-плоской линзы

Эта линзы
имеет те же значения диаметров и толщин,
что и плосковыпуклая линза;
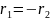
марка стекла
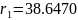
1.5521 72.64 ОК2 17.1 19.0
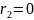
Эта линза называется линзой благоприятной формы, поскольку её сферическая аберрация мало отличается от той же аберрации в линзе, рассчитанной на минимум сферическо аберрации 3-го порядка.
Запишем уравнение первого параксиального луча:
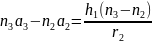
Оригинальная
запись уравнения:
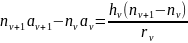
С учетом
нормировки начальных координат (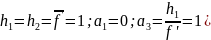 :
:
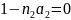
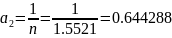
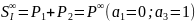
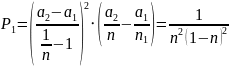
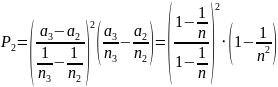
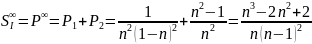
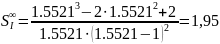
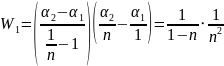
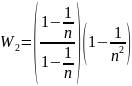
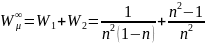

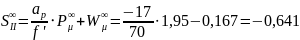
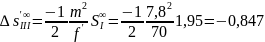
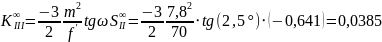
Положение входного зрачка: