
- •Тема: Функции
- •Тема: Степени и логарифмы
- •16 Найти , если
- •Тема: Тригонометрия
- •Тема: Тригонометрические уравнения
- •Тема: Производная
- •Тема: Дифференциал функции
- •Тема: Неопределённые интегралы
- •Тема: Определённый интеграл.
- •Тема: Вычисление площадей плоских фигур
- •Тема: Применение определённого интеграла к решению физических задач
- •Тема: Подготовка к зачёту
- •Тема. Основные понятия комбинаторики.
- •Вероятность события.
- •Основные теоремы теории вероятностей и их следствия.
- •Тема: Прямые и плоскости в пространстве
- •Тема: Построение сечений.
- •Тема: Перпендикулярность прямой и плоскости
- •Тема: Теорема о трёх перпендикулярах
- •Тема: Двугранный угол.
- •Тема: Подготовка к зачету
- •Тема: Многогранники.
- •Тема: Цилиндр и конус.
- •Тема: Сфера и шар
- •Тема: Площади поверхностей
- •Тема: Объёмы
Тема: Дифференциал функции
№1 Найти дифференциал функции:
а)
![]() в точке
в точке
![]()
б)
![]() в точке
в точке
![]()
№2 Найти дифференциал функции:
а)
![]() при
при
![]()
![]()
б)
при
![]()
![]()
№3 Вычислить приближенно:
а)
![]() б)
б)
![]() в)
в)
![]()
№4 Доказать, что для всех достаточно малых значений x имеет место формула:
![]()
Тема: Неопределённые интегралы
№1
Доказать, что функция
![]() является первообразной для функции
является первообразной для функции
![]() :
:
а)
![]()
![]()
б)
![]()
![]()
в)
![]()
![]()
г)
![]()
![]()
№2 Найти неопределённые интегралы:
а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
№3 Найти неопределённые интегралы:
а)
![]() б)
б)
![]() в)
в)
![]()
г)
![]() д)
д)
![]() е)
е)
![]()
ж)
![]() з)
з)
![]() и)
и)
![]()
№4 Найти неопределённые интегралы методом подстановки:
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
д)
![]() е)
е)
![]() ж)
ж)
![]() з)
з)
![]()
и)
![]() к)
к)
![]() л)
л)
![]() м)
м)
![]()
н)
![]() о)
о)
![]() п)
п)
![]() р)
р)
![]()
с)
![]() т)
т)
![]() .
.
Тема: Определённый интеграл.
№1 Вычислить интегралы:
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]() д)
д)

е)
 ж)
ж)
![]() з)
з)
![]()
№2 Вычислить интегралы, используя подстановку:
а)
![]() б)
б)
 в)
в)
![]() г)
г)
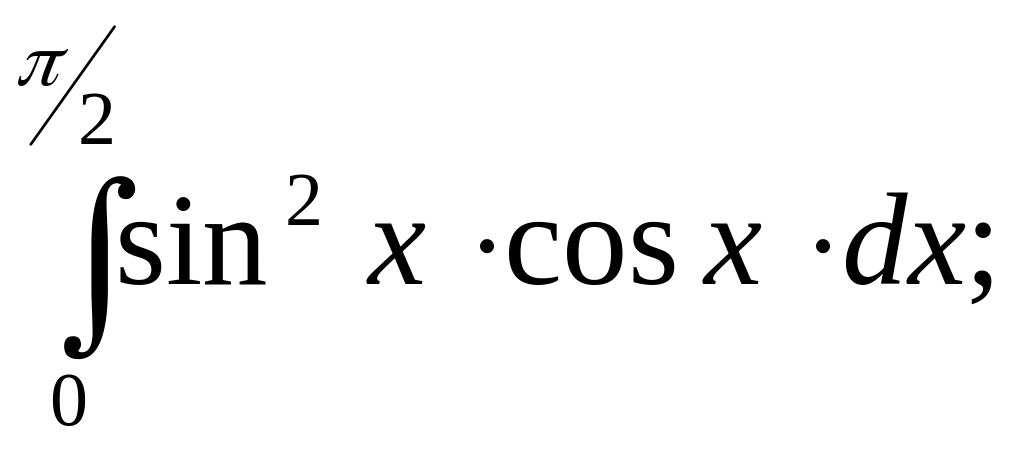
д)
![]() е)
е)
 ж)
ж)
![]()
з)
![]() и)
и)
![]()
№3 Вычислить интегралы:
а)
 б)
б)
![]() в)
в)
![]()
Тема: Вычисление площадей плоских фигур
№1 Вычислить площадь фигуры, ограниченной линиями:
а)
![]()
![]()
![]()
![]()
б)
![]()
![]()
в)
![]()
г)
![]()
д)
![]()
![]()
№2 Вычислить площадь фигуры, ограниченной линиями:
а)
![]()
![]()
б)
![]()
![]()
в)
![]()
![]()
г)
![]()
д)
![]()
![]()
е)
![]()
![]()
ж)
![]()
![]() ;
;
з)
![]()
![]()
Тема: Применение определённого интеграла к решению физических задач
№1
Тело движется прямолинейно со скоростью
![]()
![]() .
Найти
.
Найти
путь, пройденный телом за первые 5с.
№2 Скорость тела, движущегося прямолинейно, задаётся формулой
![]() .
Найти путь, пройденный телом от начала
движения до остановки.
.
Найти путь, пройденный телом от начала
движения до остановки.
№3 Вычислить работу, которую надо затратить на сжатие пружины на 0,1 м,
если для сжатия её на 0,01 м нужна сила в 78Н.
№4 Сила в 6 Н растягивает пружину на 2 см. Какую работу надо произвести,
чтобы растянуть пружину на 6 см.
Тема: Подготовка к зачёту
№1 Вычислить интегралы:
а)
 ;
б)
;
б)

№2 Вычислить площадь фигуры, ограниченной линиями:
а)
![]()
б)
![]()
![]()
Тема. Основные понятия комбинаторики.
№1. Вычислить:

№2. Сколько различных перестановок можно образовать из букв следующих слов :
а) баран; б) абракадабра?
№3. Сколькими способами можно составить расписание занятий на понедельник, если в этот день должно быть 5 уроков: алгебра, геометрия, история, география и литература, причем алгебра и геометрия не должны следовать непосредственно друг за другом?
№4. Найдите п , если
![]()
№5. Найдите область определения функции и множество ее значений
![]()
№6. В группе 30 студентов. Сколькими способами можно выделить
2-х человек для дежурства, если
а) один из них должен быть старшим;
б) старшего быть не должно?
№7. В розыгрыше первенства по футболу было сыграно 153 матча. Каждые две команды встречались между собой один раз. Сколько команд участвовало в розыгрыше первенства?
Вероятность события.
№1. По мишени производится два выстрела. Образуют ли события А (мишень поражена) и В (по крайней мере один выстрел был неудачным) полную систему событий? Являются ли события А и В несовместными?
№2. Укажите три события, которые не являются попарно несовместными, но образуют полную систему событий.
№3. Из урны, в которой находятся 3 белых, 4 черных, 5 красных шаров, наудачу вынимается один. Какова вероятность того, что вынутый шар окажется
а) белым; б) черным; в) желтым; г) красным?
№4. Бросаются две игральные кости. Какова вероятность того, что сумма очков, выпавших на двух костях, окажется равной 8?
№5. В лотерее из 50 билетов 8 выигрышных. Какова вероятность того, что среди первых пяти наугад выбранных билетов два будут выигрышными?
